Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Стандартное отклонение

Содержание

Def:Отклонение вариант от их средней Сумма таких отклонений, взятых без учета знаков и отнесенная к числу наблюдений n называется средним линейным отклонением.
Стандартное отклонение.Дисперсия. Свойства дисперсии.Коэффициент вариации. Def:Отклонение вариант от их средней Сумма таких отклонений, взятых без учета знаков Наиболее подходящим оказался показатель,построенный не на отклонениях вариант от ихсредних, а на Свойства дисперсии. Если каждую варианту совокупности уменьшить/увеличить на одно Def:Среднее квадратичное отклонение – показатель, представляющий корень квадратный из дисперсии:Дисперсия и среднее #Рассмотрим 2 вариационных ряда, распределение у которых одинаковый размах и одинаковые средние Таблица 2: Коэффициент вариации Cv.В практике довольно часто приходится сравнивать изменчивость признаков, выраженных разными Def:Cv – среднее квадратичное отклонение, выраженное в процентах от величинысредней арифметической: #Сравнивают два варьирующих признака:ииСледует ли от сюда, что 2-ой признак варьирует сильнее,чем Варьирование считается слабым, если не превосходит 10%, средним когда Cv составляет 11
Слайды презентации

Слайд 2 Def:
Отклонение вариант от их средней
Сумма таких отклонений,

Def:Отклонение вариант от их средней Сумма таких отклонений, взятых без учета

взятых без учета
знаков и отнесенная к числу наблюдений

n
называется
средним линейным отклонением.

Слайд 3 Наиболее подходящим оказался показатель,
построенный не на отклонениях вариант

Наиболее подходящим оказался показатель,построенный не на отклонениях вариант от ихсредних, а

от их
средних, а на квадратах этих отклонений,
его называют дисперсией

и выражают:

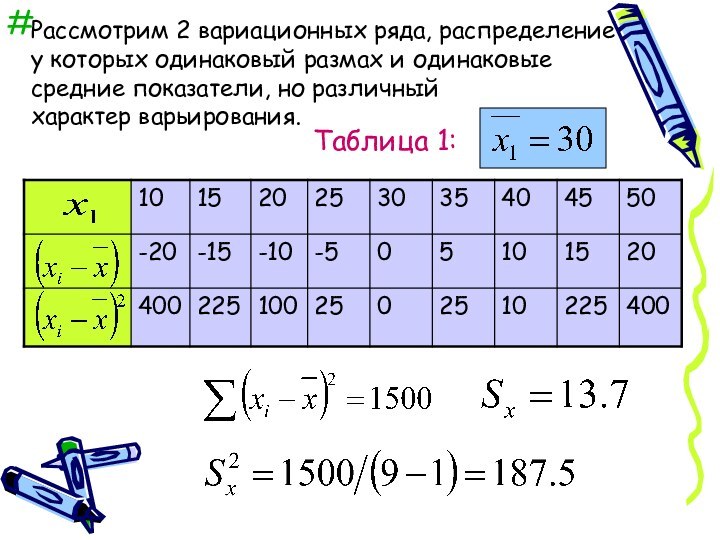
Характеризует
рассеяние точек
на числовой оси

-

Слайд 4 Свойства дисперсии.
Если каждую варианту совокупности

Свойства дисперсии. Если каждую варианту совокупности уменьшить/увеличить на одно и

уменьшить/увеличить на одно и тоже
постоянное

число, то то дисперсия не изменится:

1.

2.

Слайд 5 Def:
Среднее квадратичное отклонение –
показатель, представляющий корень
квадратный

Def:Среднее квадратичное отклонение – показатель, представляющий корень квадратный из дисперсии:Дисперсия и

из дисперсии:
Дисперсия и среднее квадратичное отклонение
наилучшим образом характеризует

не только
величину, но и специфику варьирования
признаков.

Слайд 6 #
Рассмотрим 2 вариационных ряда, распределение
у которых одинаковый

#Рассмотрим 2 вариационных ряда, распределение у которых одинаковый размах и одинаковые

размах и одинаковые
средние показатели, но различный
характер варьирования.
Таблица 1:

Слайд 7 Таблица 2:

Таблица 2:

Слайд 8 Коэффициент вариации Cv.
В практике довольно часто приходится сравнивать

Коэффициент вариации Cv.В практике довольно часто приходится сравнивать изменчивость признаков, выраженных


изменчивость признаков, выраженных разными
единицами. В таких случаях используют

не абсолютные,
а относительные показатели вариации.

Дисперсия и среднее квадратичное отклонение
как величины, выражаемые теми же единицами, что и
характеризуемый ими признак, для оценки изменчивости
разноименных величин непригодны.

Одним из относительных показателей вариации
является
коэффициент вариации.

Слайд 9 Def:
Cv – среднее квадратичное отклонение,
выраженное в процентах

Def:Cv – среднее квадратичное отклонение, выраженное в процентах от величинысредней арифметической:

от величины
средней арифметической:

Слайд 10 #
Сравнивают два варьирующих признака:
и
и
Следует ли от сюда, что

#Сравнивают два варьирующих признака:ииСледует ли от сюда, что 2-ой признак варьирует

2-ой признак варьирует сильнее,
чем 1-ый? Нет, т.к. Различны по

величине.

Вывод:

Сильнее варьирует 1-ый признак.

  • Имя файла: standartnoe-otklonenie.pptx
  • Количество просмотров: 124
  • Количество скачиваний: 0
- Предыдущая Малые социальные группы
Следующая - Чеки

Похожие презентации

7 raund 7 raund 70
Урок математики во 2 классе по теме Единица измерения длины - миллиметр план-конспект урока по математике (2 класс) Урок математики во 2 классе по теме Единица измерения длины - миллиметр план-конспект урока по математике (2 класс) 163
Устный счёт В стране Джингл – сити - 8 Устный счёт В стране Джингл – сити - 8 107
Урок и презентация по теме: Закрепление пройденного материала. методическая разработка по математике (3 класс) по теме Урок и презентация по теме: Закрепление пройденного материала. методическая разработка по математике (3 класс) по теме 120
Презентация по математике на тему Умножение и деление многозначных чисел. Что узнали, Чему научились.(4 класс) Презентация по математике на тему Умножение и деление многозначных чисел. Что узнали, Чему научились.(4 класс) 250
Полёт на Луну (3 класс) презентация к уроку по математике (3 класс) по теме Полёт на Луну (3 класс) презентация к уроку по математике (3 класс) по теме 46
trenazhyor tablitsa deleniya trenazhyor tablitsa deleniya 110
Учим таблицу умножения презентация к уроку математики (3 класс) по теме Учим таблицу умножения презентация к уроку математики (3 класс) по теме 107
Машина Тьюринга Машина Тьюринга 112
ИСПОЛЬЗОВАНИЕ ИНТЕРАКТИВНОЙ ДОСКИ НА УРОКЕ МАТЕМАТИКИ ИСПОЛЬЗОВАНИЕ ИНТЕРАКТИВНОЙ ДОСКИ НА УРОКЕ МАТЕМАТИКИ 134
Понятие модуля числа Понятие модуля числа 118
Прямая в пространстве Прямая в пространстве 82
Решение задач на противоположное движение Решение задач на противоположное движение 123
Среднее арифметическое Среднее арифметическое 206
ПРИБАВЛЕНИЕ ЧИСЛА 4 (1 КЛАСС) ПРИБАВЛЕНИЕ ЧИСЛА 4 (1 КЛАСС) 127
Цифра 7 Цифра 7 103
Координатная плоскость Координатная плоскость 123
Периметр прямоугольника. Закрепление изученного материала. (март 2019 год) методическая разработка по математике (2 класс) Периметр прямоугольника. Закрепление изученного материала. (март 2019 год) методическая разработка по математике (2 класс) 132
Решение текстовых задач Решение текстовых задач 121
Числовые и буквенные выражения Числовые и буквенные выражения 118
Задачи на проценты 5 класс Задачи на проценты 5 класс 163
Презентация к уроку математики Сравнение долей презентация к уроку по математике (3 класс) Презентация к уроку математики Сравнение долей презентация к уроку по математике (3 класс) 128
Презентация к уроку математики по теме Приёмы умножения числа 2 и на 2 Презентация к уроку математики по теме Приёмы умножения числа 2 и на 2 155
matematika - kopiya matematika - kopiya 111
Таблица сложения 1 класс Таблица сложения 1 класс 109
Конспект урока по математике 2 класс Школа России. Периметр прямоугольника план-конспект урока по математике (2 класс) Конспект урока по математике 2 класс Школа России. Периметр прямоугольника план-конспект урока по математике (2 класс) 116
Презентация - письмо цифр презентация урока для интерактивной доски по математике Презентация - письмо цифр презентация урока для интерактивной доски по математике 130
Презентация по математике Проект Математика вокруг нас (1 класс) Презентация по математике Проект Математика вокруг нас (1 класс) 141
Презентация по математике на тему Уравнения Презентация по математике на тему Уравнения 110
Цифра 5 Цифра 5 110