Слайд 2
Теоретический опрос
Объясните, какой отрезок называется перпендикуляром, проведённым из
данной точки к данной прямой.
Сформулируйте и докажите теорему о
перпендикуляре, проведённом из данной точки к данной прямой.
Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник?
Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник?
Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?
Слайд 3
Решение задач
Дано: ВЕ – медиана
АВС .
АЕ =
5 см,
ВС = 7 см,
______АС ^ BF_____________
Найти: РАВС
Слайд 4
Решение задач
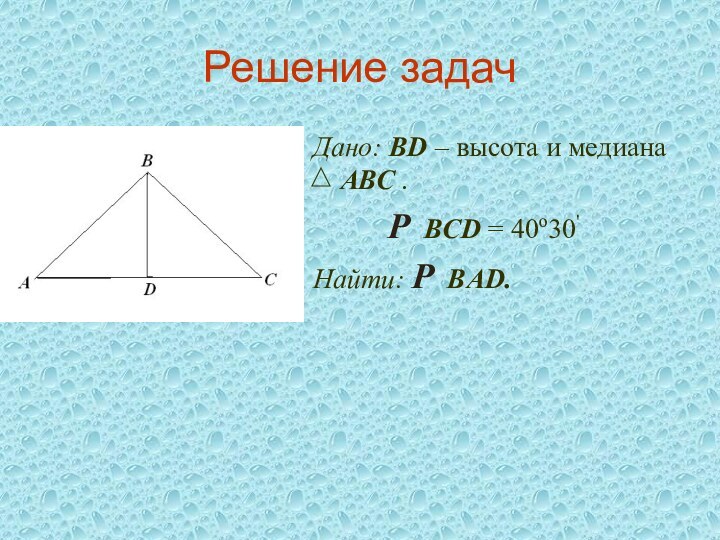
Дано: ВD – высота и медиана
АВС .
Р BCD = 40o30'
Найти: Р BАD.
Слайд 5
Практическое задание
Начертите отрезок, являющийся общей высотой для всех
треугольников, изображённых на рисунке.
Слайд 6
Определение
Треугольник, две стороны которого равны, называется равнобедренным.
Равные
стороны называют боковыми сторонами, а третью сторону – основанием
равнобедренного треугольника
Слайд 7
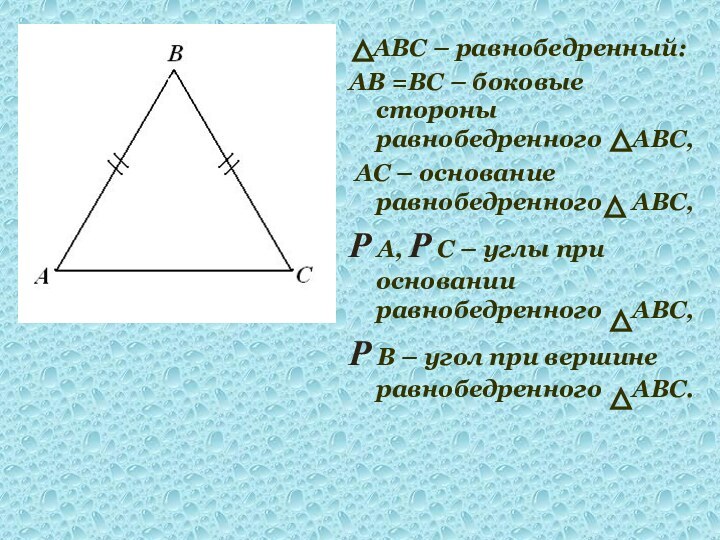
АВС – равнобедренный:
АВ =ВС –
боковые стороны равнобедренного АВС,
АС – основание
равнобедренного АВС,
Р А, Р С – углы при основании равнобедренного АВС,
Р В – угол при вершине равнобедренного АВС.
Слайд 8
Определение
Треугольник, все стороны которого равны, называется равносторонним.
АВС -
равносторонний,
АВ = ВС = АС
Слайд 9
Теорема о свойстве углов при основании равнобедренного треугольника
В
равнобедренном треугольнике углы при основании равны.
Слайд 10
Теорема о свойстве углов при основании равнобедренного треугольника
Дано:
АВС
АВ
= ВС
Доказать: Р А = Р С
Слайд 11
Доказательство:
Проведем биссектрису из вершины В к основанию АС
Далее
самостоятельно
Слайд 12
Доказательство:
Р 1 = Р 2, т.к. ВD –биссектриса)
Ю
Ю Р А = Р С.
Ч.т.д.
Проведем BD
– биссектрису АВС.
ABD = CBD
(АВ = ВС по условию,
ВD – общая сторона,
Слайд 13
Биссектриса треугольника делит угол пополам. Но а равнобедренном
треугольнике биссектриса, проведённая к основанию, обладает ещё одним очень
важным свойством. В чём заключается это свойство?
Слайд 14
Каждая ли биссектриса равнобедренного треугольника является его высотой
и биссектрисой?
Слайд 15
Является ли высота равнобедренного треугольника его биссектрисой и
медианой? Если да, то какая из трёх?
Слайд 16
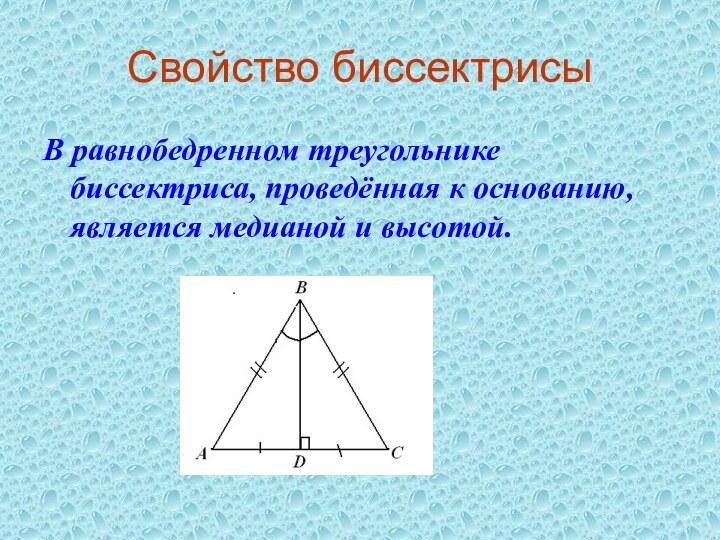
Свойство биссектрисы
В равнобедренном треугольнике биссектриса, проведённая к
основанию, является медианой и высотой.
Слайд 17
Свойство высоты
В равнобедренном треугольнике высота, проведённая к
основанию, является медианой и биссектрисой.
Слайд 18
Свойство медианы
В равнобедренном треугольнике медиана, проведённая к
основанию, является биссектрисой и высотой.
Слайд 19
Решение задач
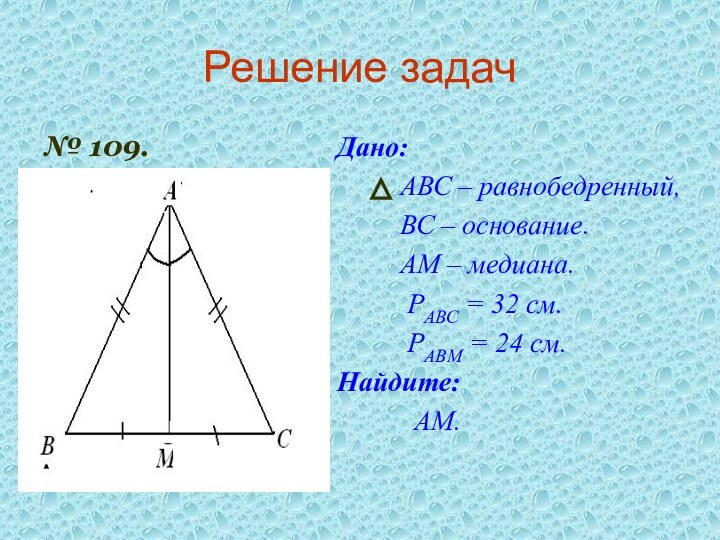
№ 109.
Дано:
АВС – равнобедренный,
ВС
– основание.
АМ – медиана.
РАВС = 32 см.
РАВМ = 24 см.
Найдите:
АМ.
Слайд 20
Решение.
АВС – равнобедренный,
ВС – основание
Ю АВ = АС;
АМ – медиана Ю ВМ =
МС.
РАВС = АВ + АС + ВС =
= 2АВ + (ВМ + МС) =
= 2 АВ + 2ВМ =
2(АВ + ВМ)=32 см Ю
Ю АВ + ВМ = 16 (см).
РАВМ = АВ + ВМ +АМ =
= 16 см + АМ = 24 см Ю
Ю АМ = 8 см.
Ответ: АМ = 8 см.
Слайд 21
№ 113
Дано: b – прямая; М, Р по
одну сторону от b; MN ^ b PQ^ b;
MN = PQ; О – середина NQ.
Р МОР = 105о.
а) доказать: Р ОМР = Р ОРМ.
б) найти: Р NОМ.
Слайд 22
тестирование
1. Медиана в равнобедренном треугольнике является его биссектрисой
и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в)
всегда неверно.
Слайд 23
тестирование
2. Если треугольник равносторонний, то:
а) он равнобедренный;
б) все
его углы равны;
в) любая его высота является биссектрисой и
медианой.
Слайд 24
тестирование
3. В каком треугольнике только одна его высота
делит треугольник на два равных треугольника?
а) в любом;
б) в
равнобедренном;
в) в равностороннем.
Слайд 25
тестирование
4. Биссектриса в равностороннем треугольнике является медианой и
высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда
неверно.
Слайд 26
тестирование
5. Если треугольник равнобедренный, то:
а) он равносторонний;
б) любая
его медиана является биссектрисой и высотой;
в) ответы а и
б неверны.
Слайд 27
тестирование
6. В каком треугольнике любая его высота делит
треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в)
в равностороннем.