Презентация на тему Производные и интегралы функций общего вида

линейной зависимости, крутизна (скорость изменения) нелинейной изменяется от точки

к точке. Местной мерой крутизны служит производная – угловой коэффициент касательной к графику функции в данной точке (здесь x0).

Процедура нахождения производной называется дифференцированием. Касательная есть предельное положение секущей при сближении точек пересечения вплоть до их слияния в одну (см. рис. 2.1). Тогда производная есть предел отношения приращений функции и аргумента при стремлении последнего (а значит, обоих) к нулю:

рис. 2.1.

(2.1)

для них производная есть непрерывная функция того же аргумента.

Это равнозначно возможности в каждой точке графика провести одну и только одну (не вертикальную!) касательную, которая плавно перекатывается по кривой при переходе от точки к точке.

Заметим, что формулу 2.1 можно изначально принять за определение производной, и так поступают авторы большинства учебников. Мы нарушили эту традицию, прибегнув вначале к наглядному геометрическому языку.

Но геометрический образ не исчерпывает всего содержания понятия производной, и теперь, введя общепринятое ее определение, мы можем в большей мере основываться на нем.

точку касания (x0, y0), через которую проходит и секущая,

заменим приращение исследуемой функции равным ему приращением по секущей: Δy=kc•Δx. При изменении положения секущей ее угловой коэффициент меняется. Выразим его как сумму постоянной и переменной частей: kc=k+Δk.
Первая есть угловой коэффициент касательной, а вторая – разность угловых коэффициентов секущей и касательной. С приближением к точке касания эта разность – по определению дифференцируемой функции – стремится к нулю. Соответственно, и приращение функции распадается на сумму двух частей: Δy = kc•dx = (k+Δk)•dx = k•dx+Δk•dx.
Обратим внимание на новое обозначение для приращения аргумента: вместо Δx использовано обозначение dx. Этим подчеркивается, что рассматривается переменное приращение и его предельный переход к нулевому значению.
Такое приращение аргумента называется его дифференциалом.

2.2. Дифференциалы

ее приращения. Он обозначается аналогично дифференциалу аргумента и определяется

как dy=k•dx; это выражение одновременно есть уравнение касательной. Итак, дифференциал функции пропорционален дифференциалу аргумента.
Вторая – нелинейная часть – есть произведение двух сомножителей, с приближением к точке касания стремящихся к нулю. Поэтому она убывает по закону второго порядка малости по сравнению с линейной, где стремится к нулю только dx. Иными словами, в достаточно малой окрестности исследуемого значения аргумента дифференцируемая функция ведет себя почти как касательная, и одну можно заменять другой с тем большей точностью, чем меньше расстояние от точки касания.
Производную можно рассматривать как отношение дифференциалов функции и аргумента, откуда следует второй способ ее обозначения:

2.2.2. Дифференциал функции.

(2.2)

двух переменных изучают после обстоятельного знакомства с техникой дифференцирования

функций одной переменной. Мы нарушим и эту традицию, потому что использование понятий из области функций нескольких переменных облегчает дифференцирование сложных функций одной переменной. Здесь не потребуется развитая теория таких функций – достаточно нескольких простейших сведений.

Последнее используется в тех случаях, когда необходимо предотвратить возможные недоразумения.

Чисто формально дифференцирование функции нескольких аргументов по одному из них ничем не отличается от дифференцирования функции одной переменной. Просто, дифференцируя по одному аргументу, остальные нужно считать постоянными. Получаемый при этом  результат называется частной производной. При обозначении дробью значок d заменяется значком ∂. Индексом указывается аргумент.

Обратим внимание на то, что при обозначении штрихом индекс относится к меняющемуся аргументу, а при обозначении дробью – к аргументу, остающемуся постоянным.

напоминает дробь, на самом деле его нужно рассматривать как

единый символ – в отличие от обычной производной функции одного переменного.

Примем произвольную точку на ней (u0, v0 ,y0) за местное начало координат (см. рис. 2.2). и образуем прямоугольную призму из четырех вертикальных плоскостей: двух координатных (на осях u, y и v, y), и двух попарно параллельных им на расстояниях, равных приращениям аргументов.

Рассмотрим линейную функцию двух независимых переменных y=f(u, v). Ее геометрический образ – плоскость в трехмерном пространстве.

горизонтальные и вертикальные катеты которых – приращения аргументов и

частные приращения функции, соответственно. (В равенстве треугольников читатель может убедиться самостоятельно).
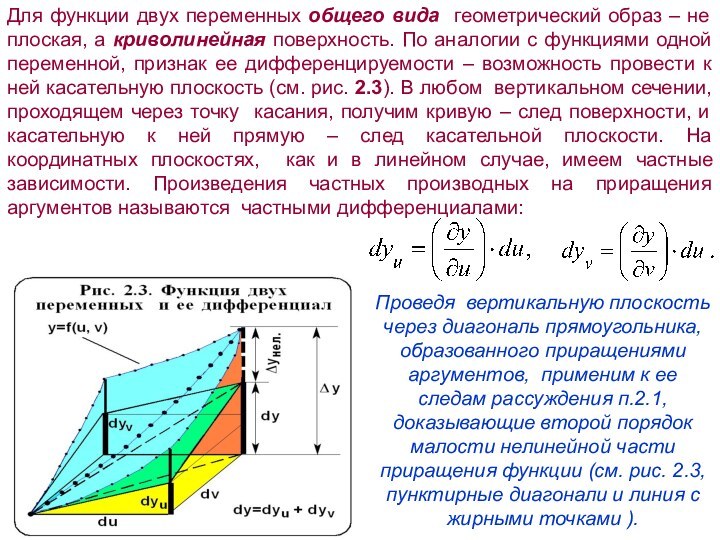
На гранях, противолежащих координатным плоскостям, эти треугольники смещены вверх на величину вертикального катета другой их пары. Отсюда следует, что полное приращение линейной функции равно сумме ее частных приращений. Это непосредственно видно из рисунка 2.2, где приращения показаны жирными вертикалями. В конечную точку вертикали Δy из местного начала координат можно попасть двумя путями – обходя участок наклонной плоскости по часовой стрелке, либо против нее. В первом случае вначале даем приращение Δyv, затем Δyu, во втором случае – вначале Δyu, затем Δyv .

В горизонтальном сечении имеем прямоугольник со сторонами Δu и Δv. При пересечении призмы плоскостью y=f(u, v) на гранях, проходящих через ось y, получим отрезки прямых – графиков частных зависимостей y от u и от v, с угловыми коэффициентами – частными производными
и , соответственно, а на противолежащих гранях – попарно

параллельные и равные им отрезки.

– не плоская, а криволинейная поверхность. По аналогии с

функциями одной переменной, признак ее дифференцируемости – возможность провести к ней касательную плоскость (см. рис. 2.3). В любом вертикальном сечении, проходящем через точку касания, получим кривую – след поверхности, и касательную к ней прямую – след касательной плоскости. На координатных плоскостях, как и в линейном случае, имеем частные зависимости. Произведения частных производных на приращения аргументов называются частными дифференциалами:    

Проведя вертикальную плоскость через диагональ прямоугольника, образованного приращениями аргументов, применим к ее следам рассуждения п.2.1, доказывающие второй порядок малости нелинейной части приращения функции (см. рис. 2.3, пунктирные диагонали и линия с жирными точками ).

окрестности точки касания приближенно описывается поведением касательной плоскости, и

погрешность такой замены стремится к нулю с приближением к этой точке.
Для общего случая, в отличие от линейного, полное приращение функции не равно сумме частных приращений. Но полный дифференциал в любом случае равен сумме частных дифференциалов:

Этот вывод естественным образом распространяется и на функции с любым числом независимых переменных.

(2.4)

Определенным интегралом, как и раньше,

назовем (на геометрическом языке) площадь фигуры, ограниченной сверху графиком функции, снизу осью абсцисс, слева и справа вертикальными границами области интегрирования. В простейшем случае мы вычисляли эту величину, как площадь прямоугольника. Этот подход используют и в общем случае, когда график криволинеен.

Для этого разбивают площадь фигуры под графиком функции на вертикальные полоски, заменяя “крышу” каждой полоски горизонтальной линией и получая тем самым ряд прямоугольников (рис. 2.4).

одной из точек в пределах данной полоски. Приближенной оценкой

интеграла при разбиении площади на n полосок служит выражение:

Оценим возможные пределы ошибки этой оценки. Величина Sn будет минимальной (максимальной), если принимать минимальное (максимальное) значение функции в пределах каждой полоски. При этом очевидно, что истинное значение площади S будет заключено между крайними оценками Smin и Smax. Их разность ΔS = Smax–Smin и можно принять за величину искомой ошибки. Она выразится суммой площадей прямоугольников, ограниченных в каждой полоске с боков ее границами, а сверху и снизу максимальным и минимальным значениями функции (см. рис. 2.4).

(2.5)

(а это достижимо при достаточно малом Δx), то ошибка

пропорциональна ширине полосок (рис.2.5). Это видно непосредственно: при разбиении полоски пополам по ширине ошибка уменьшается вдвое.

По мере увеличения n ошибка неуклонно сокращается, и в пределе, при n →∞ (или, что то же, при Δx→0), она стремится к нулю.

Суммирование площадей полосок с таким предельным переходом и называется интегрированием, и обозначается следующим образом:

(2.6)

суммы. Знак интеграла похож на вытянутое изображение латинской буквы

S – начальной в слове “сумма”, а приращение аргумента заменилось его дифференциалом. Снизу и сверху от знака интеграла указаны нижний и верхний пределы интегрирования. Их смысл совпадает с линейным случаем.
Еще раз отметим отличия от простейшего случая (гл. 1). Там не нужно было разбивать измеряемую площадь на полоски – ее значение вычислялось сразу по элементарной формуле. Поэтому не было и операций суммирования и перехода к пределу. Теперь, из-за нелинейности, в этом возникла необходимость, и в каждой полоске мы проделываем то, что раньше проделывали сразу со всей площадью.

В главе 1 выяснилось, что для линейных функций действия

дифференцирования и интегрирования взаимно обратны. Нетрудно догадаться, что это относится и к любым другим функциям. Осталось это доказать. Чтобы определить производную интеграла по верхнему пределу, составим выражение для разности двух интегральных сумм: ΔS = Sn–Sn-1 =fn•Δx
(величину Δx указываем без индекса, считая ее одинаковой для всех полосок). Отношение приращений функции и аргумента выразится как ΔS/Δx = fn , то есть равно значению подынтегральной функции на верхней границе суммирования. При Δx→0 эта граница превращается в верхний предел интегрирования. Иными словами, производная определенного интеграла по его верхнему пределу равна подынтегральной функции, и тем самым наше предположение доказано. Выражение для производной после перехода к пределу выразится следующим образом:

интегрирование, а аргумент в выражении для производной – величина

x, по ней ведется дифференцирование. Нередко используют и запись:

Она не является ошибочной, но нужно помнить, что переменная x под знаком интеграла и переменная x- верхний предел – это разные переменные, лишь одинаково обозначенные и откладываемые по одной и той же оси. Разница в том, что на результат при интегрировании влияют все значения “немой” переменной между верхним и нижним пределами, в то время, как при дифференцировании нас интересует только значение верхнего предела, и в окончательном выражении стоит именно оно.

(2.7)

(2.7а)

формула Ньютона-Лейбница (ФНЛ), позволяющая вычислять значения определенного интеграла через

значение неопределенного интеграла поочередной подстановкой в него верхнего и нижнего пределов интегрирования и последующего вычитания второго из первого.

В действительности эта формула по-настоящему нужна именно для общего случая, и теперь требуется доказать, что она к нему применима. Главное для этого доказательства уже сделано: выяснено, что для любых функций производная интеграла по верхнему пределу равна подынтегральному выражению. Следовательно, площадь криволинейной трапеции с переменной правой границей выражается графиком первообразной, для которой исходная функция есть производная.

2.2.3. Теорема Ньютона-Лейбница

пределом интегрирования!), от которого отсчитывается эта площадь, соответствует нулевому

значению первообразной. Определенный интеграл – площадь между заданными границами – равен разности значений первообразной на этих границах (рис. 2.6):

(2.8)

Рис.2.6. Первообразная и формула Ньютона-Лейбница для общего случая.

и прежде, геометрический смысл ФНЛ состоит в том, что

при выборе любой первообразной значение определенного интеграла равно разности значений первообразной на верхнем и нижнем пределах интегрирования.
Переход от одной из них к другой равнозначен вертикальному перемещению треугольника, гипотенуза которого теперь стала криволинейной (ср. рис. 1.6 и 2.7).

подстановки пределов интегрирования в выражение первообразной:

Все, что было сказано о первообразных в главе 1, остается в силе и здесь. Первообразных для данной функции существует неограниченное количество, и все они могут быть получены произвольным вертикальным смещением любой из них.
Еще раз напомним: при подстановке левого и правого пределов используется одна и та же первообразная. Серьезный источник трудностей для начинающих в понимании смысла ФНЛ – в том, что начало отсчета для используемой первообразной не обязано совпадать с левой границей интервала интегрирования. Обычно отсчет ведется от x=0, но и это совсем не обязательно, если удобнее окажется другой вариант.

(2.8а)

Итак, мы познакомились с обобщениями понятий производной и

интеграла на нелинейный случай. Такая последовательность изложения совершенно не соответствует истории их возникновения. Они изначально были созданы именно для общего случая, ибо для линейных функций все, что требуется, с успехом делалось без использования этих понятий задолго до их появления. Когда же они появились, линейные задачи сразу превратились в их вырожденный частный случай.

Но учебная задача отличается от научной, ибо новичков затрудняют не только проблемы, волнующие первооткрывателей, и часто даже в первую очередь не они. Автор счел полезным нарушить традицию, чтобы максимально облегчить усилия начинающих.