Слайд 2
При изучении геометрии в школе можно
установить взаимосвязи между геометрическими понятиями и окружающим миром.
Продемонстрируем это на примере изучения свойств «золотого сечения».
С древности, наблюдая за окружающей природой и создавая произведения искусства, люди искали закономерности, которые позволяли бы определить прекрасное, то есть пытались вывести «формулу красоты».
Слайд 3
Ряд «формул красоты» известен.
Это правильные геометрические формы: квадрат, круг, равносторонний треугольник и
т.д.; это – законы симметрии.
Можно привести множество примеров присутствия симметрии в окружающем нас мире.
Симметрию легко обнаружить в окружающем нас мире.
Слайд 5
Эстетическое наслаждение, получаемое человеком при наблюдении совершенных
форм предмета, объясняется не только выполнением законов симметрии, но
и присутствием так называемой «божественной» пропорции «золотого сечения» в соотношении частей, на которые предмет делится естественным образом.
Слайд 6
Соблюдение пропорций в природе означает соблюдение
определенных соотношений между размерами отдельных частей растений.
«Золотое
сечение» являлось критерием гармонии и красоты во времена Пифагора и в эпоху Возрождения.
Слайд 7
Определение
«Золотым сечением» называют такое деление отрезка на
две неравные части, при котором длина меньшей части так
относится к длине большей части, как длина большей части к длине всего отрезка, т.е. при «золотом сечении отрезка АВ точкой С имеет место следующая золотая пропорция:
A C B
Слайд 8
«Золотое сечение» встречается в растительном мире.
Рассматривая расположение трех подряд идущих пар листьев
на общем стебле растения, можно заметить, что между первой и третьей парой вторая находится в месте «золотого сечения».
Слайд 10
Скульптурные творения греческих мастеров Фидия, Политекта,
Мирона, Праксителя по праву считаются эталонами красоты человеческого тела.
Оценивая фигуру того или иного человека мы невольно сравниваем ее с этими признанными эталонами.
По мнению многих искусствоведов, художников, скульпторов и архитекторов эпохи Возрождения, основные пропорции человеческого тела подчинены законам «золотого сечения».
Слайд 12
Каждая отдельная часть тела – голова, рука,
кисть и т.д. – также делятся по закону «золотого
сечения» на естественные части.
Так, разделив в отношении «золотого сечения» отрезок, заключенный между макушкой и адамовым яблоком, мы получим точку, лежащую на линии бровей.
При дальнейшем золотом делении образовавшихся частей получим последовательно кончик носа, конец подбородка.
Слайд 14
Строение руки и кисти также согласуется с принципом
«золотого сечения»
Слайд 15
На прямоугольники, стороны которых соотносятся приблизительно
как 0,6:1,
обратили внимание очень давно. На
рисунке дано изображение храма Парфенон в Афинах.
Даже сейчас, когда он стоит в развалинах, это одно из самых красивых сооружений мира.
Храм построен в эпоху расцвета древнегреческой математики и его красота основана на строгих математических законах.
Слайд 16
Если фасад Парфенона вписать в прямоугольник, то он
окажется золотым прямоугольником.
Слайд 17
Сенат в Кремле
Известный русский архитектор М.
Казаков в своем творчестве широко использовал «золотое сечение». Его
талант был многогранным, но в большей степени он раскрылся в многочисленных осуществленных проектах жилых домов и усадеб. Например, «золотое сечение» можно обнаружить в архитектуре здания сената в Кремле.
А Г Р А М М А
Пятиконечная
звезда-пентаграмма всегда привлекала внимание людей совершенством формы.
Ей около 3000 лет.
Ее первые изображения донесли до нас вавилонские глиняные таблички.
Слайд 19
Из Древней Вавилонии в Средиземноморье, как полагают,
звездчатый пятиугольник привез ПИФАГОР и сделал его символом жизни
и здоровья, а также тайным опознавательным знаком.
В средние века пентаграмма предохраняла от "нечистой силы", что, впрочем, не мешало считать ее "лапой ведьмы".
И в наши дни пятиконечная звезда красуется на флагах и гербах многих стран.
Слайд 20
Форму правильного пятиугольника можно встретить в живой
природе. Такую форму имеют, например, морские звезды. Ученые археологи
обнаружили на камне отпечаток части древнего растения.
Можно было различить лишь два лепестка какого-то цветка. Восстановив внешний вид этого цветка, было отмечено, что в его построении присутствует правильный пятиугольник, а значит и золотое сечение.
Слайд 21
Пример использования «золотого сечения» в живописи
Слайд 22
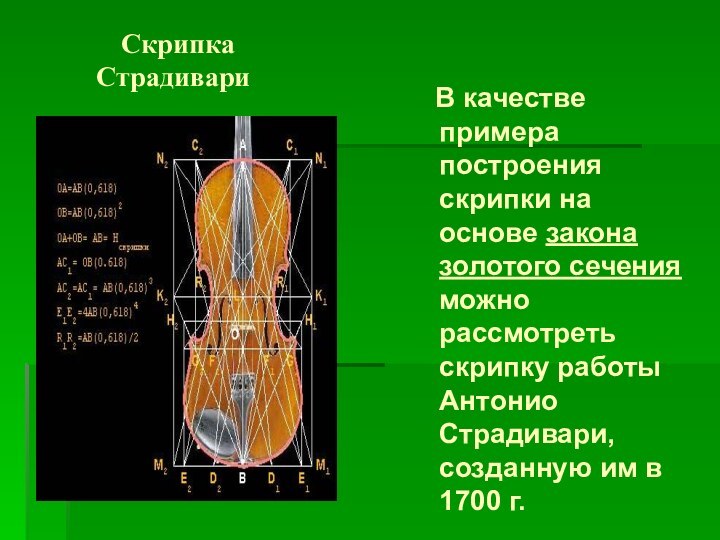
Скрипка
Страдивари
В качестве примера
построения скрипки на основе закона золотого сечения можно рассмотреть
скрипку работы Антонио Страдивари, созданную им в 1700 г.