Слайд 2
План лекции:
Актуальность темы. Общие понятия в теории проверки
гипотез. Ошибки 1 и 2 рода.
Подходы к сравнению
критериев. Минимаксный подход. Байесовский подход.
Построение оптимальных критериев. Критерий отношения правдоподобия
Сравнение эмпирических и теоретических распределений.
Заключение
Слайд 3
Актуальность темы.
Одним из наиболее важных разделов математической статистики
является проверка статистических гипотез.
Слайд 4
Проверка статистических гипотез
Статистической называется гипотеза о виде неизвестного
распределения или о параметрах известных распределений, формулируемая на основе
выборки.
Примеры статистических гипотез:
генеральная совокупность распределена по нормальному закону;
математические ожидания двух выборок из генеральной совокупности равны.
Гипотезы формулируются только для параметров генеральной совокупности
Слайд 5
Гипотезы, в основе которых нет никаких допущений о
конкретном виде закона распределения, называют непараметрическими, в противном случае
– параметрическими.
Гипотезу, утверждающую, что различие между сравниваемыми характеристиками отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями в выборках, на основании которых производится сравнение, называют нулевой (основной) гипотезой (Н0).
Наряду с основной гипотезой рассматривают и альтернативную (конкурирующую, противоречащую) ей гипотезу Н1. И если нулевая гипотеза будет отвергнута, то будет иметь место альтернативная гипотеза.
Слайд 6
Гипотезу называют простой, если она однозначно характеризует параметр
распределения случайной величины. Например, если λ является параметром экспоненциального
распределения, то гипотеза Н0 о равенстве λ =10 – простая гипотеза.
Сложной называют гипотезу, которая состоит из конечного или бесконечного множества простых гипотез. Гипотеза Н0 о том, что математическое ожидание нормального распределения равно двум при неизвестной дисперсии, является сложной.
Слайд 7
Проверка гипотезы основывается на вычислении некоторой
случайной величины – критерия, точное или приближенное распределение которого
известно. Обозначим эту величину через K, ее значение является функцией от элементов выборки
K=K(x1, x2, …, xn).
Процедура проверки гипотезы предписывает каждому значению критерия одно из двух решений – принять или отвергнуть гипотезу. Тем самым все выборочное пространство и соответственно множество значений критерия делятся на два непересекающихся подмножества S0 и S1. Если значение критерия K попадает в область S0, то гипотеза принимается, а если в область S1, – гипотеза отклоняется.
Слайд 8
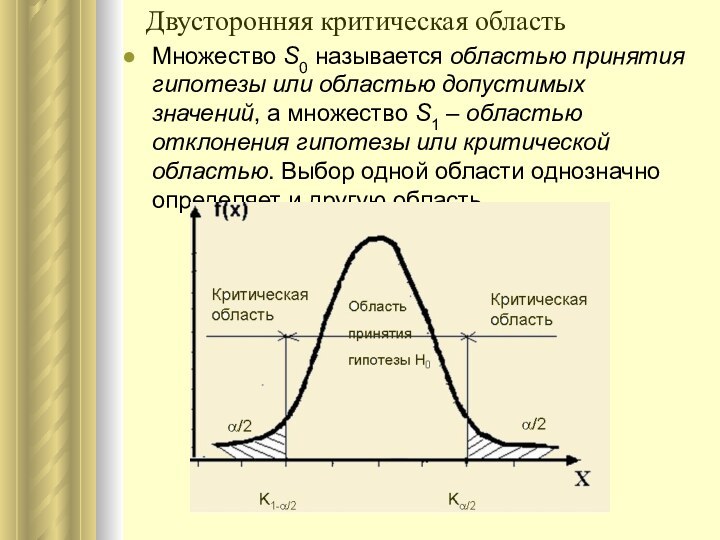
Множество S0 называется областью принятия гипотезы или областью
допустимых значений, а множество S1 – областью отклонения гипотезы
или критической областью. Выбор одной области однозначно определяет и другую область.
Двусторонняя критическая область
Слайд 9
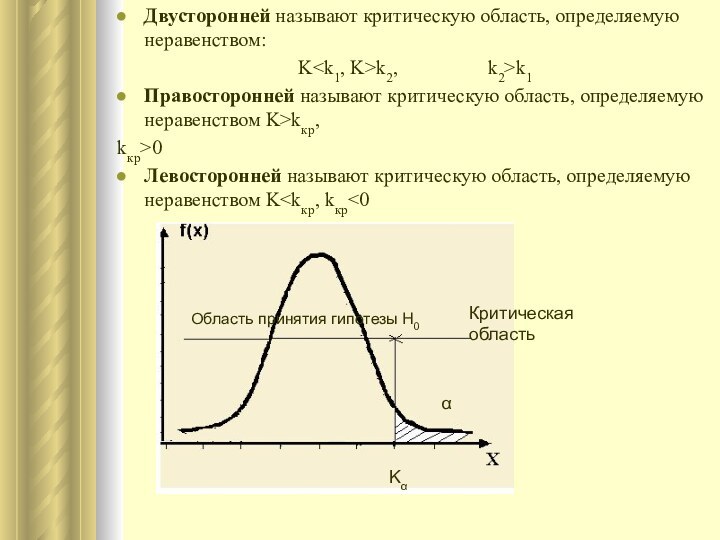
Двусторонней называют критическую область, определяемую неравенством:
Kk2,
k2>k1
Правосторонней называют
критическую область, определяемую неравенством K>kкр,
kкр>0
Левосторонней называют критическую область, определяемую неравенством K
Слайд 10
Принятие или отклонение гипотезы Н0 по случайной выборке
соответствует истине с некоторой вероятностью и, соответственно, возможны два
рода ошибок.
Ошибка первого рода возникает с вероятностью α тогда, когда отвергается верная гипотеза Н0 и принимается конкурирующая гипотеза Н1.
Ошибка второго рода возникает с вероятностью β в том случае, когда принимается неверная гипотеза Н0, в то время как справедлива конкурирующая гипотеза Н1.
Слайд 11
Доверительная вероятность – это вероятность не совершить ошибку
первого рода и принять верную гипотезу Н0. Вероятность отвергнуть
ложную гипотезу Н0 называется мощностью критерия.
Слайд 12
Алгоритм проверки статистических гипотез
Располагая выборочными данными (x1, x2,
…, xn) формулируют нулевую гипотезу (Н0) и конкурирующую гипотезу
(Н1).
Задают уровень значимости (ошибка 1 рода).
Рассматривается выборочная статистика наблюдений (критерий К)
На основании выборки (x1, x2, …, xn) определяют эмпирическое значение критерия (Кэмп)
В зависимости от вида альтернативной гипотезы по соответствующей таблице выбирают квантили критерия для двусторонней или односторонней критической области (Ккр)
Если значения критерия попадают в критическую область (Кэмп> Ккр), то нулевая гипотеза отвергается и принимается альтернативная гипотеза H1.
Если значения критерия Кэмп< Ккр, нулевая гипотеза не отвергается.
Слайд 13
Пример. Имеется выборка объёма n = 1 из
нормального распределения Na,1 и две простые гипотезы H1={a=0} и
H2={a=1}.
Рассмотрим при некотором b ∈ R следующий критерий:
K(X1) = H1, если X1 ≤ b,
H2, если X1 > b.
Изобразим на графике соответствующие гипотезам плотности распределений и вероятности ошибок первого и второго рода критерия K
α=PH1(X1>b), β=PH2(X1 ≤ b)
Подходы к сравнению критериев
Слайд 14
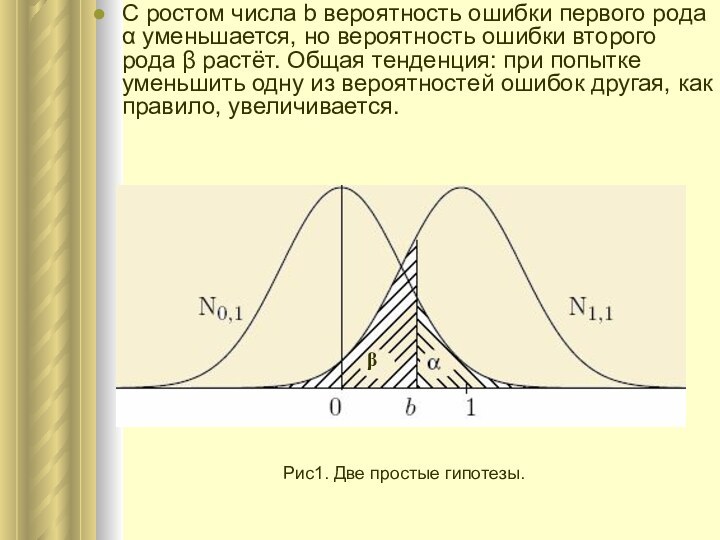
C ростом числа b вероятность ошибки первого рода
α уменьшается, но вероятность ошибки второго рода β растёт.
Общая тенденция: при попытке уменьшить одну из вероятностей ошибок другая, как правило, увеличивается.
Рис1. Две простые гипотезы.
β
Слайд 15
П р и м е р. Пусть любое
изделие некоторого производства оказывается браком с вероятностью p. Контроль
продукции допускает ошибки: годное изделие бракует с вероятностью α, а бракованное пропускает (признаёт годным) с вероятностью β.
Если ввести для проверяемого изделия гипотезы H1 = {изделие годное} и H2 = {изделие бракованное}, а критерием выбора одной из них считать контроль продукции, то α -вероятность ошибки первого рода этого критерия, а β -второго рода:
α = PH1(K = H2) = P(контроль забраковал годное изделие);
β = PH2(K = H1) = P(контроль пропустил бракованное изделие);
Упражнение. Вычислить вероятности ошибок первого и второго рода того же критерия, если гипотезы занумеровать иначе:
H1 = изделие бракованное, H2 = изделие годное.
Слайд 16
Подходы к сравнению критериев
Пусть сравниваем две простые гипотезы.
Имеется два критерия с вероятностями ошибок 1 и 2
рода: α(К1), β(К1) и α(К2), β(К2).
Минимаксный подход.
Говорят, что критерий К1 не хуже К2 в смысле минимаксного подхода, если:
max{α (К1),β (К1)}≤ max{α (К2),β (К2)}
Минимаксный критерий имеет самую маленькую «наибольшую ошибку» max{α (К1), β(К1)} среди всех критериев.
Слайд 17
Байесовский подход.
Этот подход применяют в двух случаях:
а) если
известно априори, что с вероятностью r справедлива гипотеза H1,
а с вероятностью s=1- r -гипотеза H2,
б) если задана «линейная функция потерь»: потери от ошибочного решения равны r если происходит ошибка 1 рода и s - если второго. r + s не обязательно равно 1, но потери можно свести к 1 нормировкой r'=r/(r+s) s'=s/(r+s).
Пусть априорные вероятности или потери заданы. Говорят, что критерий К1 не хуже К2 в смысле байесовского подхода, если:
rα(К1)+sβ(К1)≤ rα (К2)+sβ (К2)
Байесовский критерий имеет самую маленькую «средневзвешенную ошибку» rα(К1)+sβ(К1) среди всех прочих критериев.
Слайд 18
По формуле полной вероятности это есть вероятность ошибки
критерия в случае а) или математическое ожидание потерь в
случае б).
Выбор наиболее мощного критерия (НМК).
Ошибки 1 и 2 рода не равноправны. Если зафиксировать ошибку 1 рода, то лучшим будет считаться критерий с наименьшей ошибкой 2 рода.
Построение оптимальных критериев.
Оптимальные во всех трех смыслах (минимаксные, байесовские и наиболее мощные) критерии могут быть построены в самом общем случае простым выбором различных констант в одном и том же критерии - критерии отношения правдоподобия.
Слайд 19
Критерий отношения правдоподобия
Пусть имеется выборка X=X1, X2, …
, Xn (набор независимых, одинаково распределенных величин), и имеются
две гипотезы о распределении Xi:
H1- Xi имеют распределение F1
H2- Xi имеют распределение F2.
Оба распределения либо дискретны, либо непрерывны
Соответствующие функции правдоподобия (ф.п.=плотность распределения выборки)
Слайд 20
Отношением правдоподобия называется частное:
Если нужно получить критерий с
заданной ошибкой 1 рода α или иметь возможность варьировать
и размер и мощность критерия, следует рассмотреть класс похожих критериев, введя свободный параметр (1 или какая-то константа С).
Если вторая плотность в C раз превышает первую, принимается вторая гипотеза, в противном случае принимается гипотеза H1. Kc(X)-критерий отношения правдоподобия.
Слайд 21
Да
Нет
Закон распределения-нормальный?
М±σ, М±m,
M (95% ДИ)
Сравнение 2-х выборок по
критерию Стьюдента
Корреляция по Пирсону
Параметрическая статистика
Ме [25%-75%],
Мo, Min-Max
Сравнение 2-х
выборок по критериям Манна-Уитни, Вилкоксона
Корреляция по Спирмену
Непараметрическая статистика
Слайд 22
Сравнение эмпирических и теоретических распределений
Нулевая гипотеза (Н0)- эмпирическое
распределение студентов по росту не отличается от нормального распределения
Выбираем
уровень значимости для проверки гипотезы α=0,05 (5% ошибки)
Гипотезу проверяем по критерию tэмп для коэффициентов асимметрии и эксцесса
По таблице вероятностей для нормального распределения выбираем квантиль критерия для двусторонней критической области (tкр=1,96)
Если значения критерия попадают в критическую область (tэмп > 1,96), то нулевая гипотеза отвергается и принимается альтернативная гипотеза H1.
Если значения критерия tэмп < 1,96, нулевая гипотеза не отвергается. Распределение студентов по росту не отличается от нормального распределения
Слайд 23
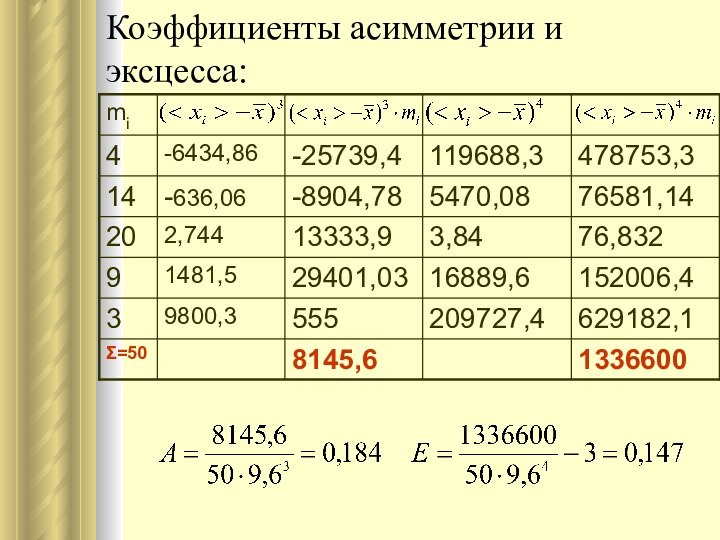
Коэффициенты асимметрии и эксцесса:
Слайд 24
Вычислим по выборке коэффициенты асимметрии и эксцесса
Критерий нормированного
отклонения t показывает отклонение параметра по выборке от значения
в генеральной совокупности, выраженное в единицах среднеквадратической ошибки.
Так как в генеральной совокупности для нормального распределения коэффициенты асимметрии и эксцесса равны 0, то
Слайд 25
Ошибки коэффициентов асимметрии и эксцесса (n=50):
Слайд 26
Вывод: т.к. 0,56
Нулевая гипотеза не отвергается – распределение студентов по
росту соответствует нормальному закону с уровнем ошибки 0,05 (5%).
Слайд 27
Критерии согласия
Пусть задана некоторая случайная величина, измеряющая отклонение
эмпирического распределения от теоретического.
Критерии согласия принимают или отвергают
основную гипотезу исходя из величины этой функции отклонения.
Критерии χ2 Пирсона, Колмогорова, Смирнова, Мизеса, Шапиро-Уилки и т.д.
Слайд 28
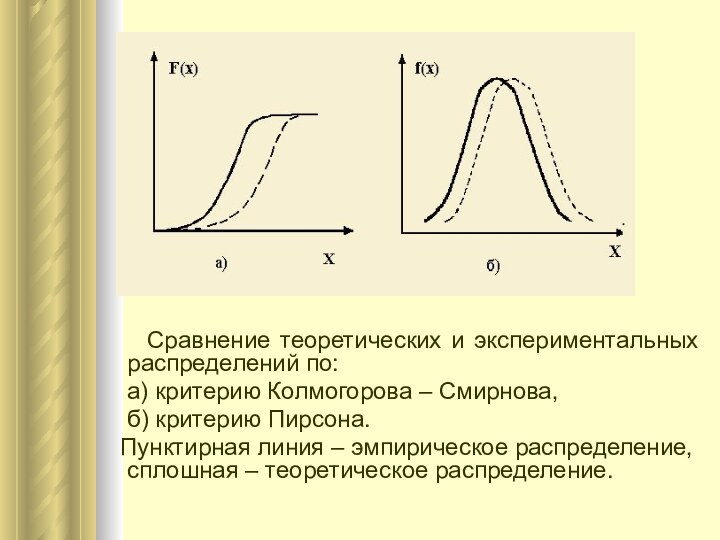
Сравнение теоретических и экспериментальных распределений
по:
а) критерию Колмогорова – Смирнова,
б) критерию Пирсона.
Пунктирная линия – эмпирическое распределение, сплошная – теоретическое распределение.
Слайд 29
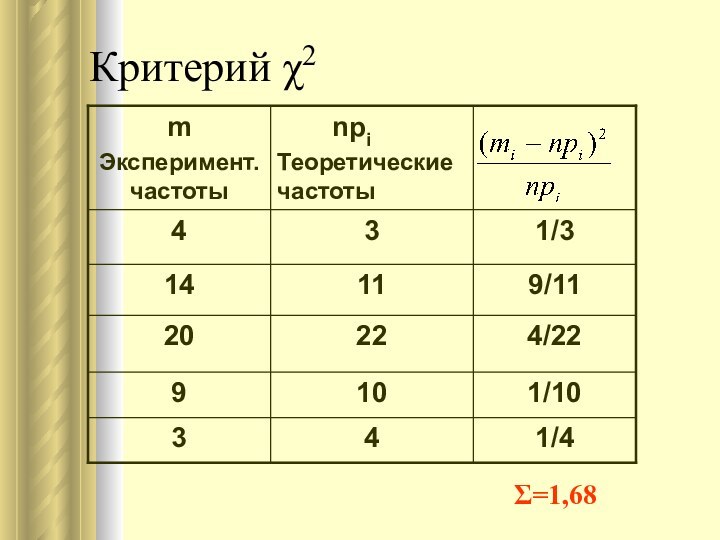
Проверка гипотезы о нормальном распределении генеральной совокупности по
критерию χ2 .
Для проверки гипотезы будем сравнивать эмпирические mi
(наблюдаемые) и теоретические npi (вычисленные в предположении нормального распределения) частоты.
В качестве критерия проверки нулевой гипотезы принимаем случайную величину χ2 :
Затем по таблице критических точек распределения χ2 (таблица Приложения) по заданному уровню значимости α и числу степеней свободы найдем критическое значение χ2кр.(α,df).
Если χ2эмп.≤χ2кр.(α,df), то считаем, что данный критерий оснований для отклонения гипотезы не дает, а в противном случае считаем, что гипотеза не согласуется с экспериментальными данными и ее надо отвергнуть.
Слайд 30
Критерий Пирсона
где mi – экспериментальные частоты
попадания значения случайной величины в интервал,
npi
– теоретические частоты.
Слайд 31
Вероятность попадания значения случайной величины в интервал от
а до b:
причем Ф(–t) = 1– Ф(t)
=Ф(t2)-Ф(t1)
Слайд 33
Число степеней свободы – это общее число величин,
по которым вычисляются соответствующие статистические показатели, минус число тех
условий, которые связывают эти величины, то есть уменьшают возможности вариации между ними. Число степеней свободы определяется по следующей формуле:
df=k–r–1, где k – число интервалов, r – число параметров предполагаемого распределения. Для нашего случая r=2, следовательно, df=k–3.
По заданному уровню значимости (α) и числу степеней свободы df, находим критическое значение χ2кр (α,df).
Слайд 34
χ2кр (α=0,05,df=2)=5,99
1,68
студентов по росту подчиняется нормальному закону.
Допущения:
Число интервалов =5 и
более
mi≥n⋅α, в противном случае интервалы можно объединить с соседними
Слайд 35
Заключение
Нами рассмотрены:
Основные положения проверки статистических гипотез.
Принципы построения оптимальных
критериев.
Примеры проверки гипотезы о законе распределения по критерию асимметрии
и эксцесса и критерию χ2.
Слайд 36
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА:
Основная литература:
Попов А.М. Теория вероятней и математическая
статистика /А.М. Попов, В.Н. Сотников. – М.: ЮРАЙТ, 2011.
– 440 с.
Гмурман В. Е. Теория вероятностей и математическая статистика: учебное пособие / В.Е. Гмурман. – М. : Высш. шк., 2011. – 479 с.
Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике / В.Е. Гмурман. – М. : Высш. шк., 2011. – 404 с.
Балдин К. В. Основы теории вероятностей и математической статистики : учебник / К. В. Балдин. – М. : Флинта, 2010. – 488с.
Учебно–методические пособия:
Шапиро Л.А., Шилина Н.Г. Руководство к практическим занятиям по медицинской и биологической статистике Красноярск: ООО «Поликом». – 2003.