- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Прямоугольные треугольники
Содержание
- 2. Для продолжения работы выберинеобходимый раздел.Свойства прямоугольных треугольниковПризнаки равенства прямоугольных треугольниковПроверь себя
- 3. Прямоугольные треугольникиОпределение:Треугольник, в котором один угол прямой, называется прямоугольным.гипотенузакатеткатетАВС С – прямой.
- 4. Реши задачи по готовым чертежамАВСНайти А и
- 5. 1. Докажите, что в прямоугольном треугольнике сумма
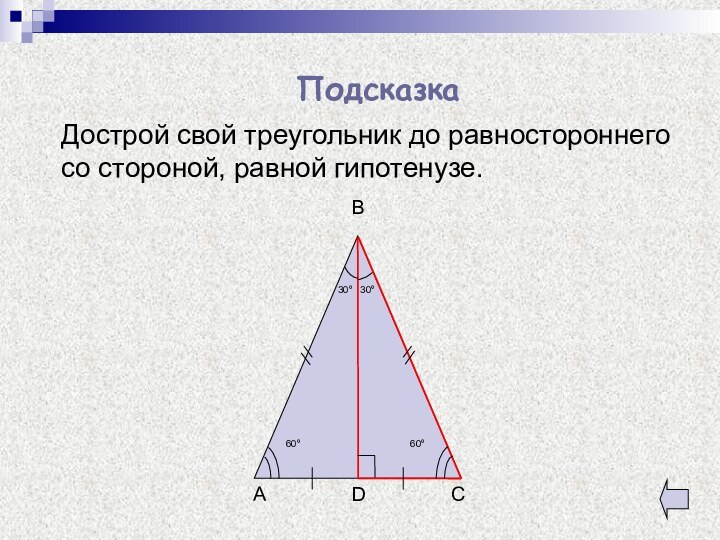
- 6. Дострой свой треугольник до равностороннего со стороной, равной гипотенузе.Подсказка
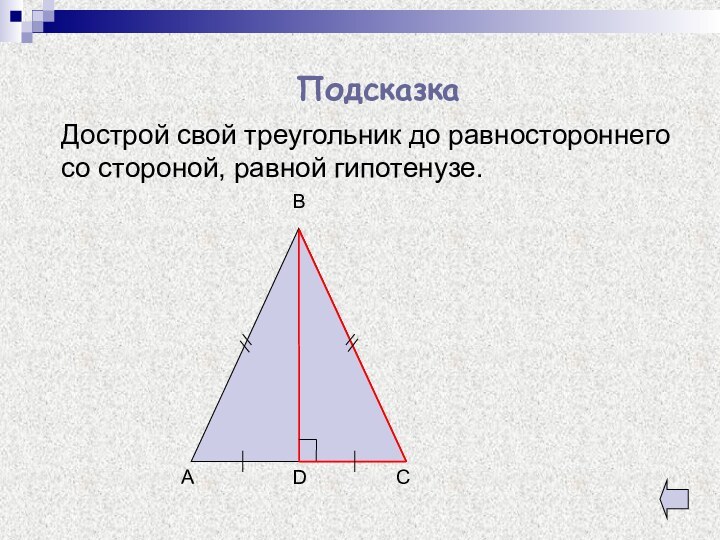
- 7. Дострой свой треугольник до равностороннего со стороной, равной гипотенузе.ПодсказкаDACB
- 8. Свойства прямоугольных треугольниковЭто интересно!1. Сумма двух
- 9. Уголковый отражатель.Падающий лучОтражённый лучзеркалозеркалоПадающий луч и отражённый луч параллельны.Уголковый отражатель используется в технике.
- 10. Реши задачи по готовым чертежамАВС1. Найти ВС.1060°Ответ:
- 11. признакиравенствапрямоугольныхтреугольников
- 12. Первый признак равенства прямоугольных треугольниковАСВА1С1В1Дано: треугольники АВС
- 13. Второй признак равенства прямоугольных треугольников(по катету и
- 14. Третий признак равенства прямоугольных треугольниковДано: треугольники АВС
- 15. Четвёртый признак равенства прямоугольных треугольниковДано: треугольники АВС
- 16. ВDCЕА46°44°Доказать: ВСCDCЕDАВ35°55°Найти: АСЕНВСА60°Дано: ВН=4 см.Найти: АН.47°АВОСDДано: АВ
- 17. Проверь себя!Какой треугольник называется прямоугольным?Как называются стороны
- 18. Скачать презентацию
- 19. Похожие презентации
Для продолжения работы выберинеобходимый раздел.Свойства прямоугольных треугольниковПризнаки равенства прямоугольных треугольниковПроверь себя







Слайд 2
Для продолжения работы выбери
необходимый раздел.
Свойства прямоугольных
треугольников
Признаки
равенства
Слайд 3
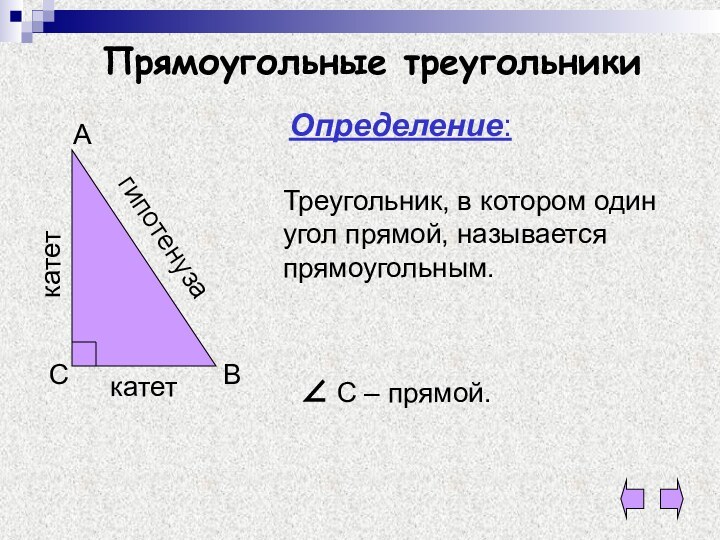
Прямоугольные треугольники
Определение:
Треугольник, в котором один
угол прямой, называется прямоугольным.
гипотенуза
катет
катет
А
В
С
С – прямой.
Слайд 4
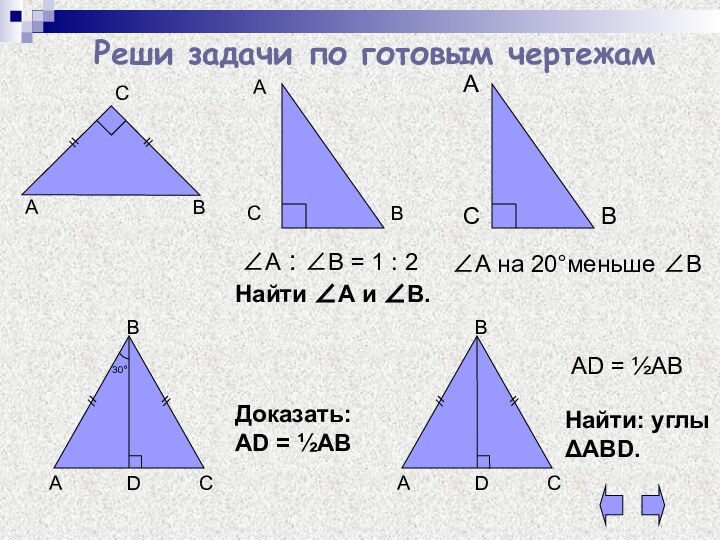
Реши задачи по готовым чертежам
А
В
С
Найти А и В.
А
С
С
В
А
: В = 1 : 2
А на 20°меньше В
А
В
30°
D
A
C
B
Доказать:
AD = ½ABD
A
C
B
AD = ½AB
Найти: углы ABD.
Слайд 5 1. Докажите, что в прямоугольном треугольнике сумма двух
острых углов равна 90°.
2. Докажите, что катет прямоугольного треугольника,
лежащий против угла в 30°, равен половине гипотенузы.3. Докажите, что если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
А
С
В
А
С
В
А
С
В
30°
подсказка
подсказка
Слайд 8
Свойства прямоугольных
треугольников
Это интересно!
1. Сумма двух острых углов
прямоугольного треугольника равна 90°.
2. Катет прямоугольного треугольника, лежащий против
угла в 30°, равен половине гипотенузы.3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
Слайд 9
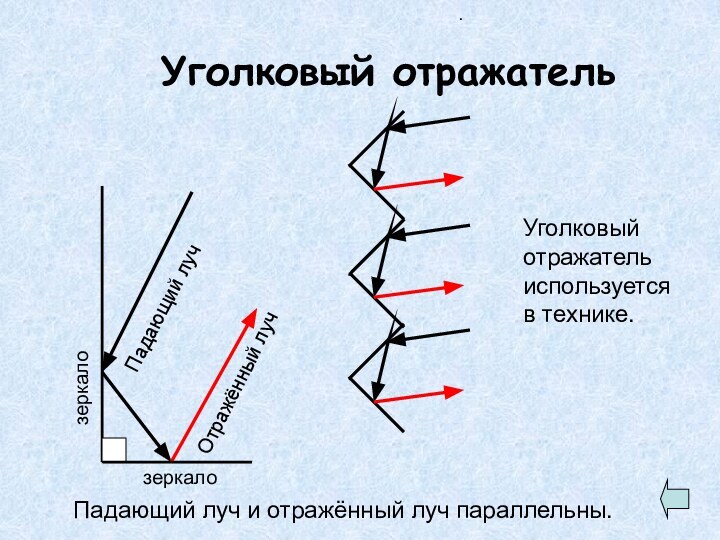
Уголковый отражатель
.
Падающий луч
Отражённый луч
зеркало
зеркало
Падающий луч и отражённый луч
параллельны.
Уголковый отражатель используется в технике.
Слайд 10
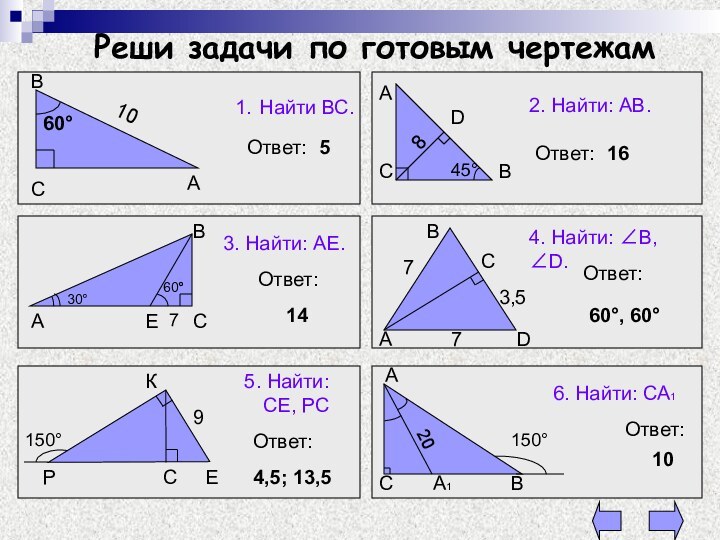
Реши задачи по готовым чертежам
А
В
С
1. Найти ВС.
10
60°
Ответ:
5
А
С
В
D
8
45°
2.
Найти: АВ.
Ответ:
16
150°
150°
20
А
С
А1
В
6. Найти: СА1
Ответ:
10
К
Р
С
Е
9
5. Найти: СЕ, РС
Ответ:
4,5; 13,5
7
7
3,5
А
D
C
B
4. Найти:
, D.Ответ:
60°, 60°
А
Е
С
В
60
30°
3. Найти: АЕ.
7
Ответ:
14
Слайд 12
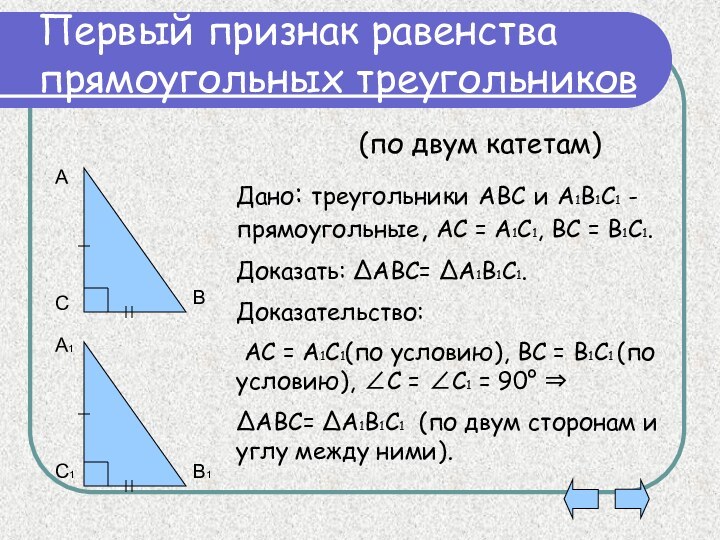
Первый признак равенства прямоугольных треугольников
А
С
В
А1
С1
В1
Дано: треугольники АВС и
А1В1С1 - прямоугольные, АС = А1С1, ВС = В1С1.
Доказать:
АВС= А1В1С1.Доказательство:
АС = А1С1(по условию), ВС = В1С1 (по условию), С = С1 = 90°
АВС= А1В1С1 (по двум сторонам и углу между ними).
(по двум катетам)
Слайд 13
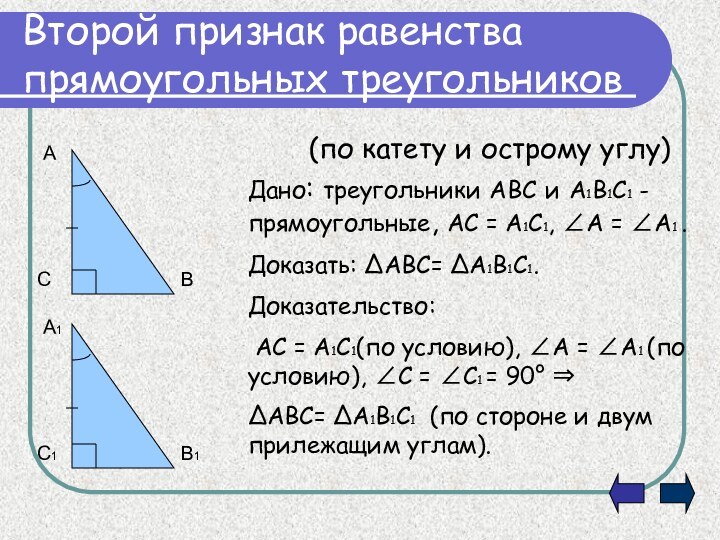
Второй признак равенства прямоугольных треугольников
(по катету и острому
углу)
Дано: треугольники АВС и А1В1С1 - прямоугольные, АС =
А1С1, А = А1 .Доказать: АВС= А1В1С1.
Доказательство:
АС = А1С1(по условию), А = А1 (по условию), С = С1 = 90
АВС= А1В1С1 (по стороне и двум прилежащим углам).
А
С
В
Слайд 14
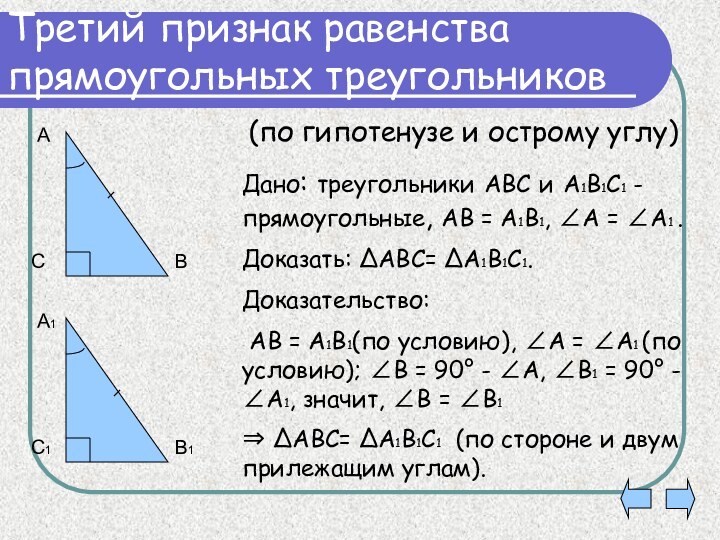
Третий признак равенства прямоугольных треугольников
Дано: треугольники АВС и
А1В1С1 - прямоугольные, АВ = А1В1, А = А1
.Доказать: АВС= А1В1С1.
Доказательство:
АВ = А1В1(по условию), А = А1 (по условию); В = 90° - А, В1 = 90° - А1, значит, В = В1
АВС= А1В1С1 (по стороне и двум прилежащим углам).
(по гипотенузе и острому углу)
А
С
В
А1
С1
В1
Слайд 15
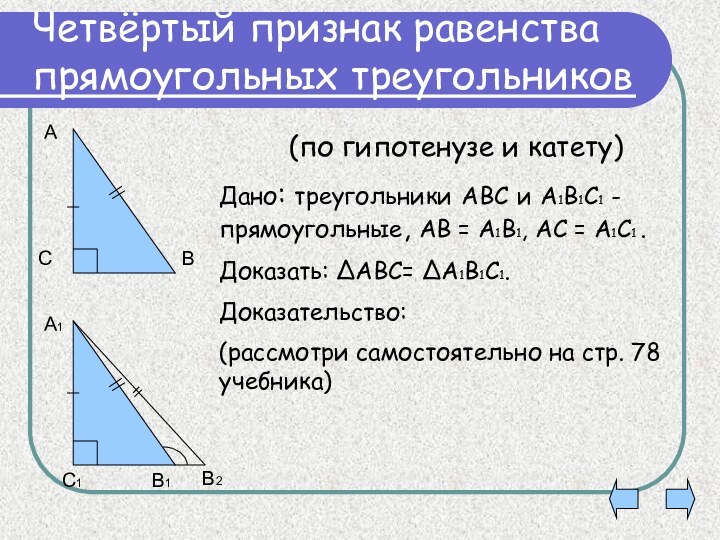
Четвёртый признак равенства прямоугольных треугольников
Дано: треугольники АВС и
А1В1С1 - прямоугольные, АВ = А1В1, АС = А1С1
.Доказать: АВС= А1В1С1.
Доказательство:
(рассмотри самостоятельно на стр. 78 учебника)
(по гипотенузе и катету)
В2
А
С
В
А1
С1
В1
Слайд 16
В
D
C
Е
А
46°
44°
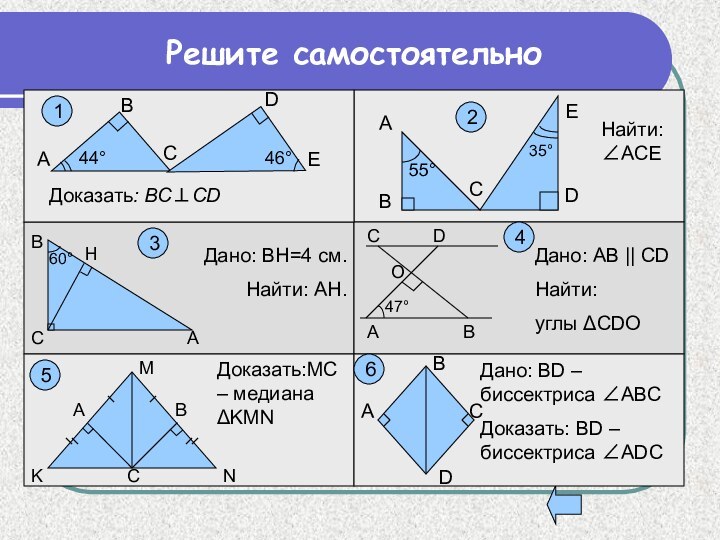
Доказать: ВСCD
C
Е
D
А
В
35°
55°
Найти: АСЕ
Н
В
С
А
60°
Дано: ВН=4 см.
Найти: АН.
47°
А
В
О
С
D
Дано: АВ ||
CD
Найти:
углы CDO
Доказать:MC – медиана KMN
D
C
A
B
Дано: BD – биссектриса
АВСДоказать: BD – биссектриса АDС
Решите самостоятельно
1
2
3
4
5
6
Слайд 17
Проверь себя!
Какой треугольник называется прямоугольным?
Как называются стороны прямоугольного
треугольника?
Верно ли, что сумма двух острых углов прямоугольного треугольника
равна 90°?Сформулируйте свойства прямоугольного треугольника.
Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и острому углу.
Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и катету.
Сформулируйте признак равенства прямоугольных треугольников по двум катетам.
Сформулируйте признак равенства прямоугольных треугольников по катету и острому углу.
В основе чего лежит одно из свойств прямоугольного треугольника?





























