Презентация на тему Рациональные числа

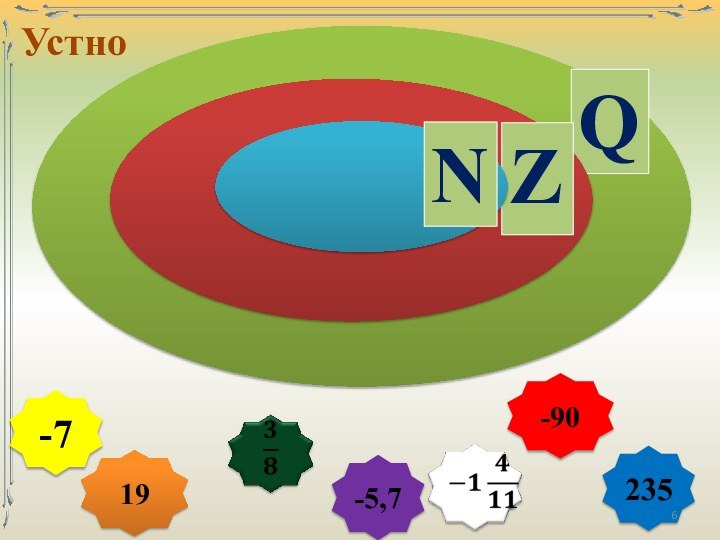
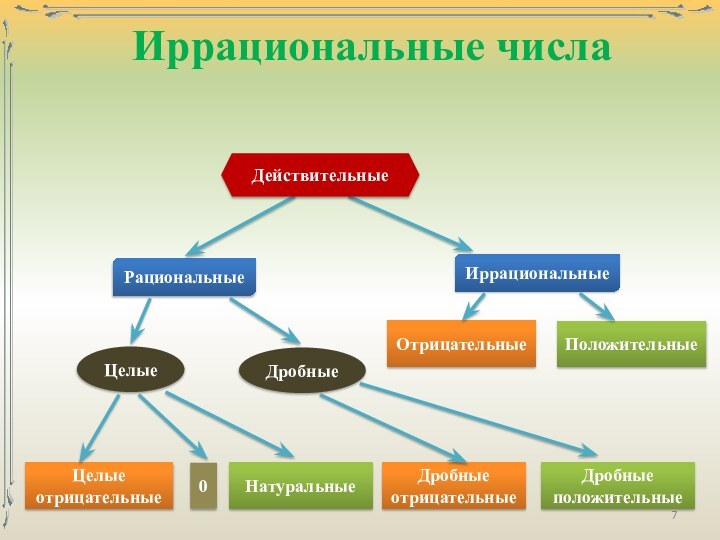
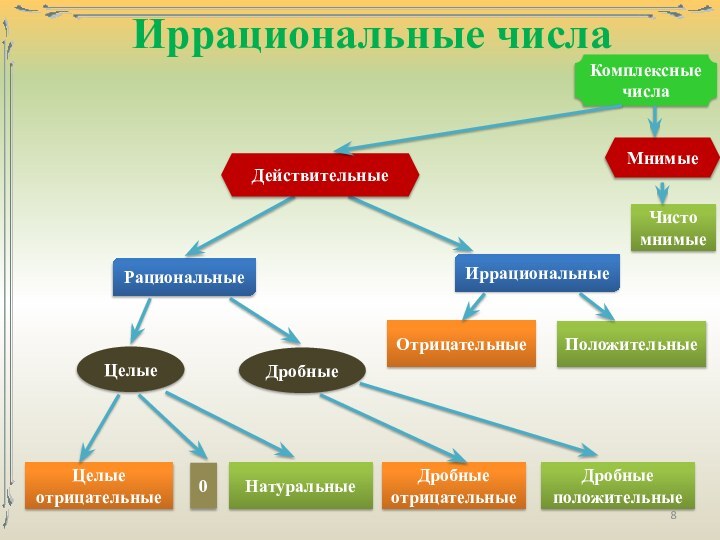
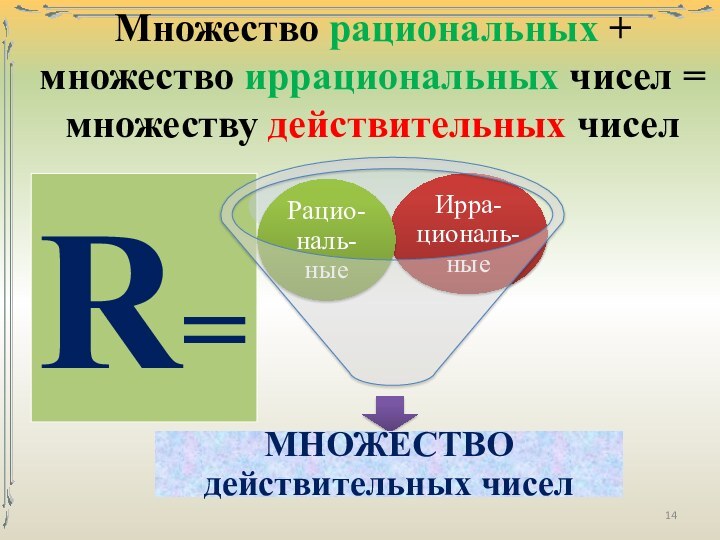
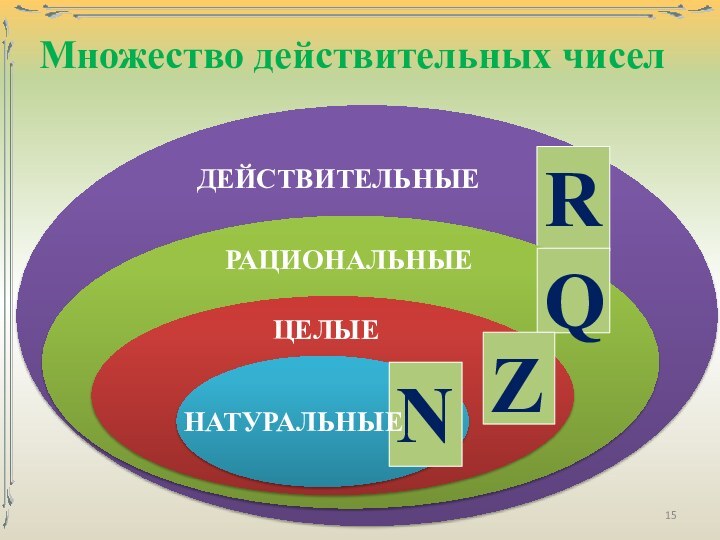
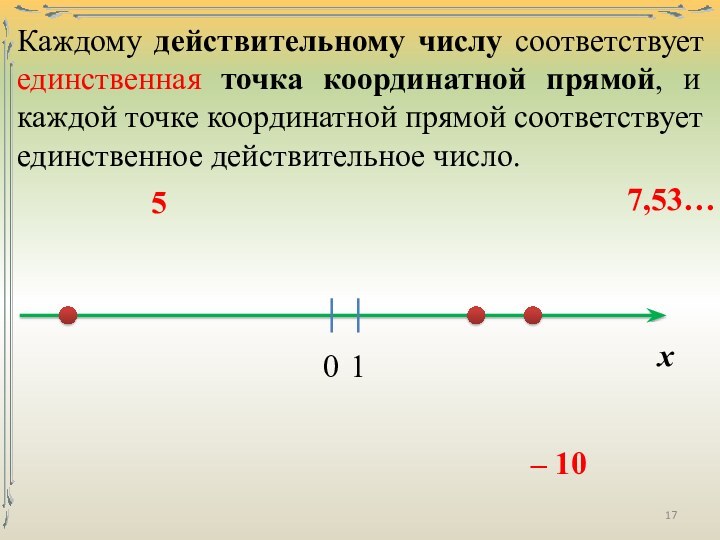
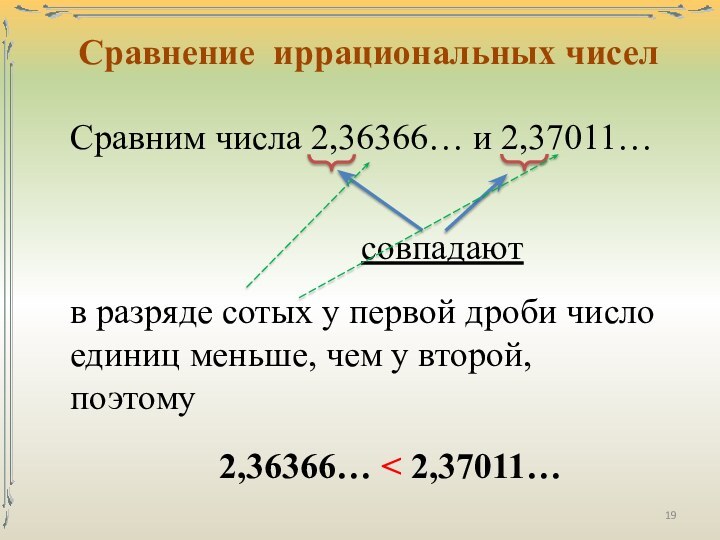
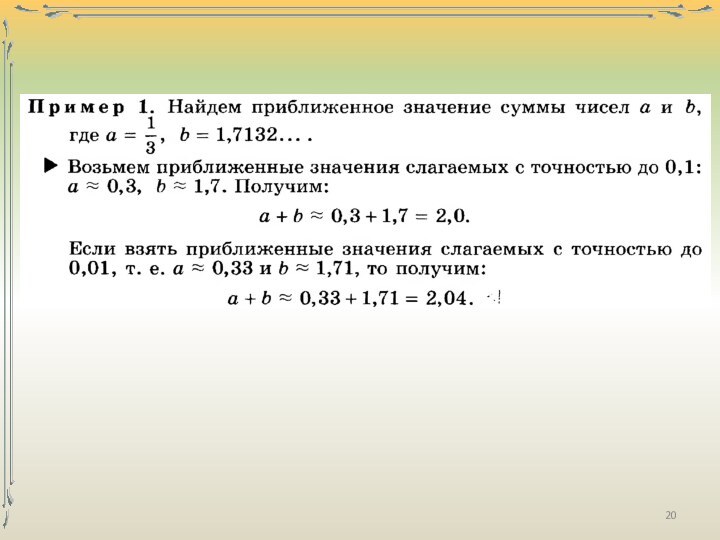
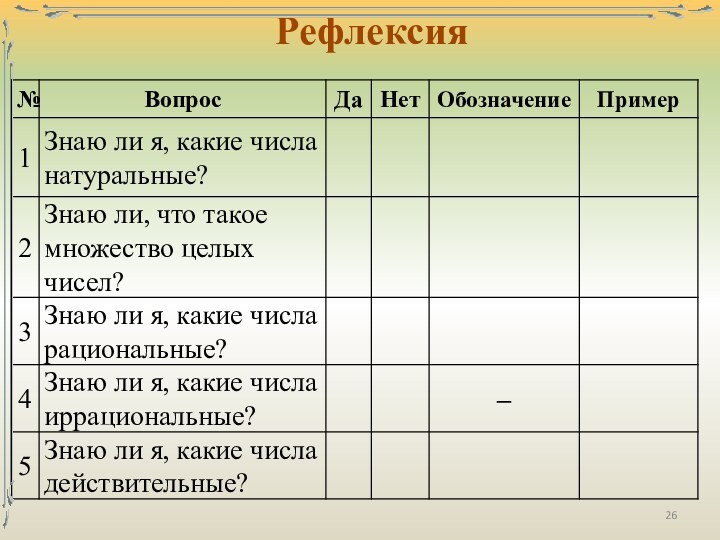
числа – числа, возникающие естественным образом при счёте.
Существуют два подхода

к определению натуральных чисел — числа, используемые при:
перечислении (нумеровании) предметов 
(первый, второй, третий, …);
обозначении количества предметов (нет предметов, один предмет, два предмета, …).

1-й танк

2-й танк

3-й танк

N

числа и нуль
-5, -4, -3, -2, -1, 0, 1,

2, 3, 4, 5

Z

пришли к выводу, что нет ни целого, ни дробного

числа, выражающего диагональ квадрата со стороной 1. Это вызвало кризис в математической науке: диагональ у квадрата есть, а длины у неё нет!
Математики нашли выход из этой ситуации: раз имеющегося запаса чисел – целых и дробных – не хватает для выражения длин отрезков, значит, нужны какие-то новые числа. Так появились иррациональные числа.

учебником стр.63 – 64
п. 11.
Устно ответить на вопросы:
Как можно

измерить длину любого отрезка?
Как можно получить более точный результат (с точностью до 0,1; 0,01 и 0,001?
Какие числа окажутся в результате измерений?

Иррациональные числа

равен 2.

действительных чисел
R=

множеством действительных чисел.
…, 3,010010001…, …
0
…, – 5,020022000222...,…

и каждой точке координатной прямой соответствует единственное действительное число.
х
5
0
1
–

10

7,53…

прямой существует взаимно однозначное соответствие.

разряде сотых у первой дроби число единиц меньше, чем

у второй, поэтому

2,36366… < 2,37011…

281 (а, в, д).
№ 285, № 286.
Упражнения

выпускают 120 ракет. Сколько ракет выпустят за 4 секунды.

иррациональными?
– Из каких чисел состоит множество действительных чисел?

е), № 282