- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему
Содержание
- 2. Одной из основных и простейших фигур в
- 3. Дано:Найти: углы ∆ACH. 1.∆ABC - равнобедренный с основанием AB,CH – медиана, ∟ АСВ =80°.Устно решить задачу.
- 4. 2.Устно решить задачу.Дано: ABCD - параллелограмм,AB =
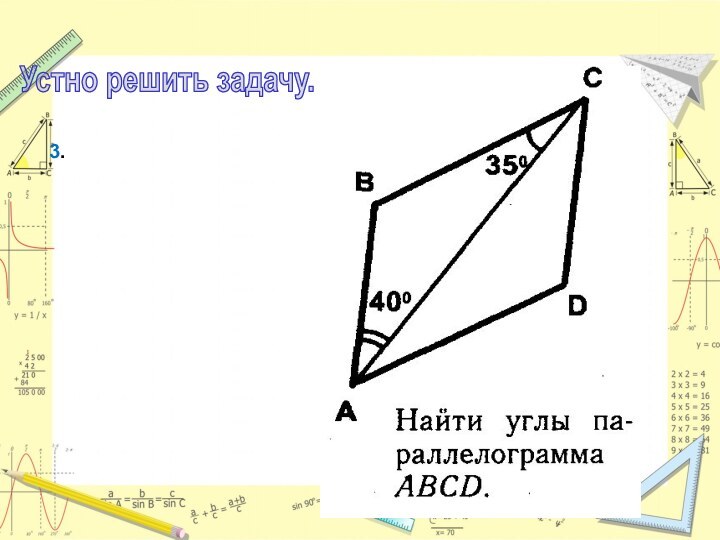
- 5. 3.Устно решить задачу.
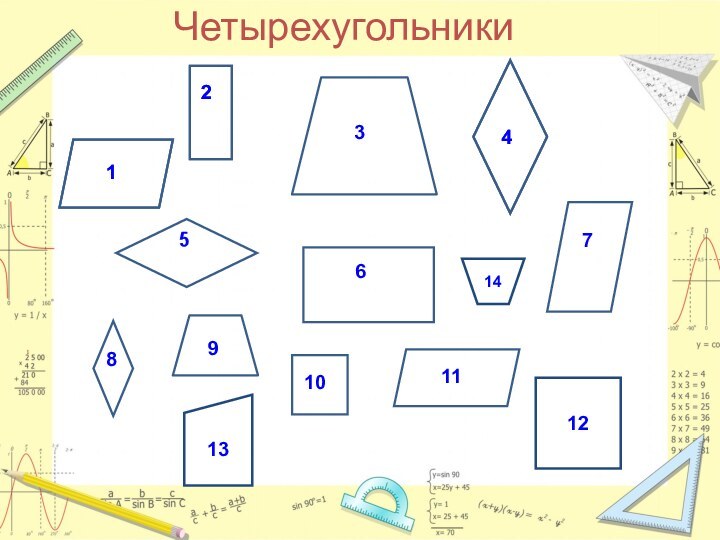
- 6. Четырехугольники 121314
- 7. Четырехугольникипараллелограммтрапеция39121314
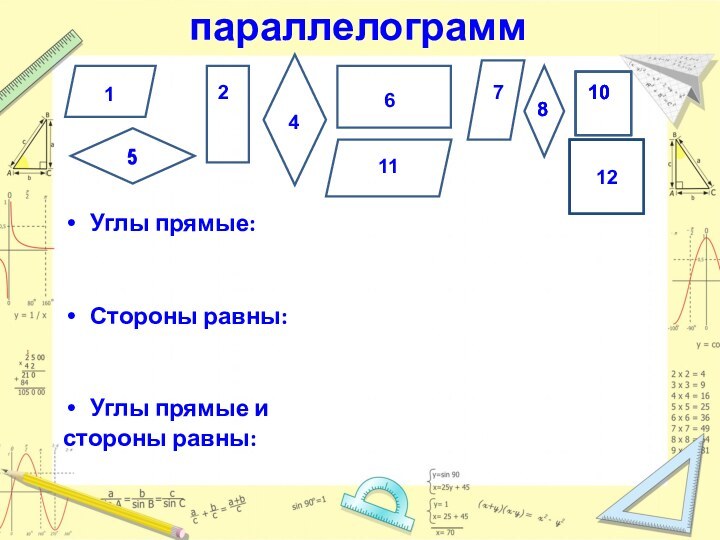
- 8. параллелограммУглы прямые:Стороны равны:Углы прямые истороны равны:121212
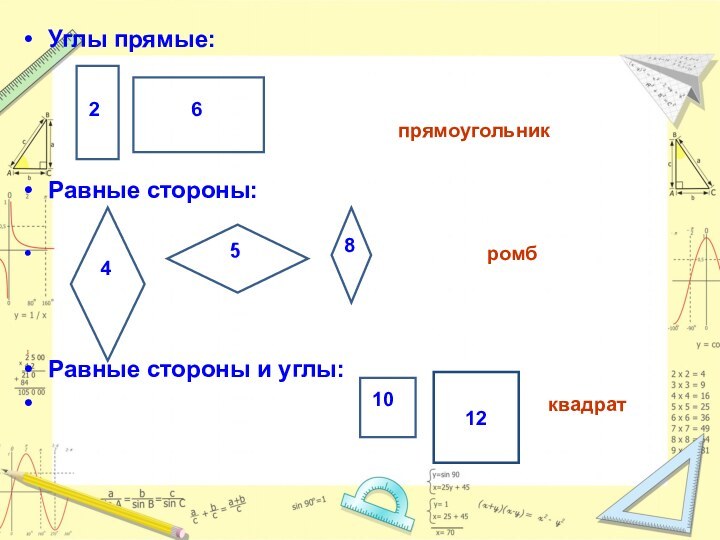
- 9. Углы прямые:
- 10. ПрямоугольникРомбКвадратТема урока:
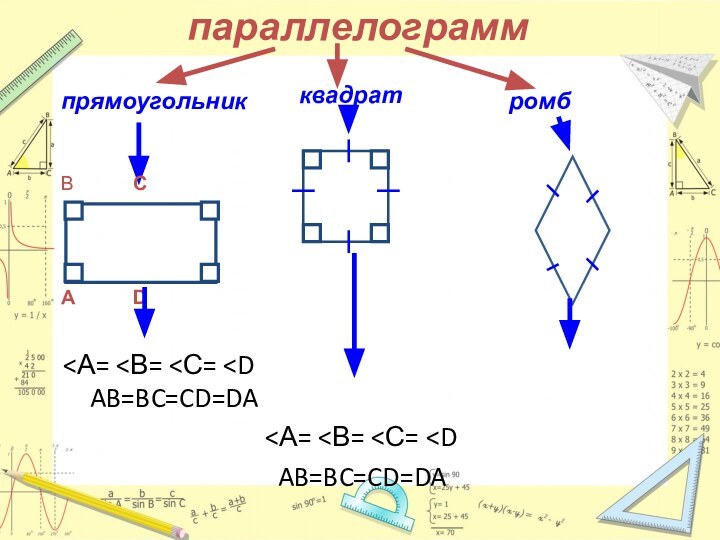
- 11. параллелограмм
- 12. ОВАСDДано: ABCD - прямоугольник,АВ = 3см, AD=
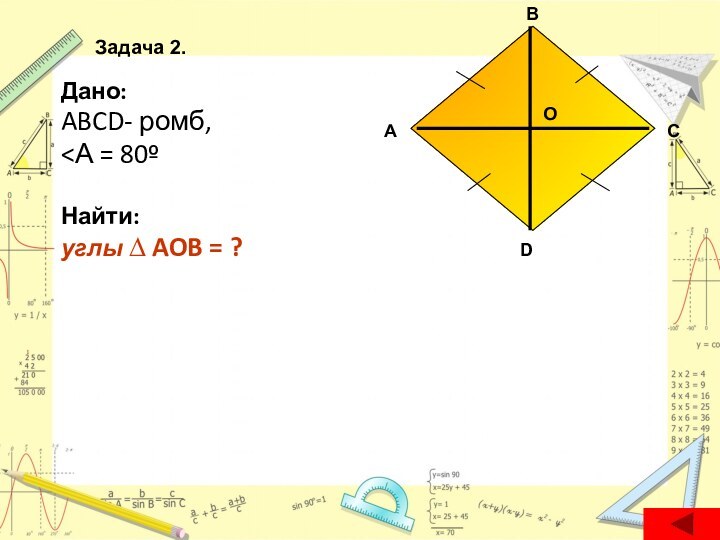
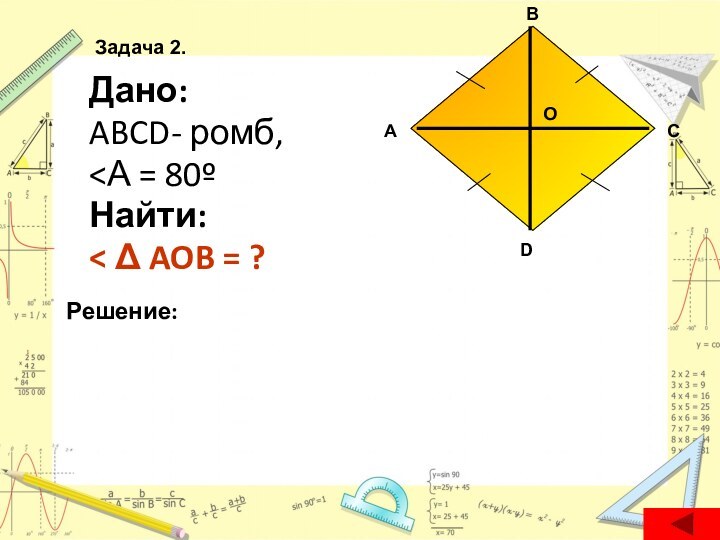
- 13. Дано:ABCD- ромб,
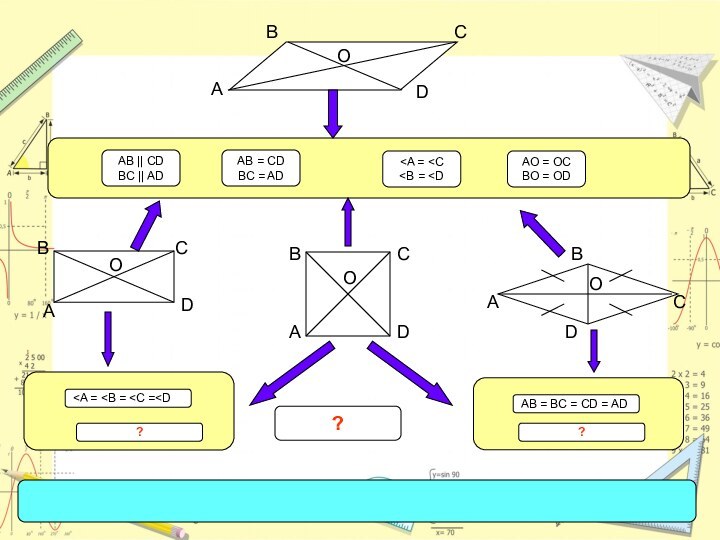
- 14. OAB = CD BC = ADAB || CD BC || ADAO = OC BO = OD
- 15. Цели урока: дать определение, и установить свойства и признаки:прямоугольника, ромба, квадрата.
- 16. Исследовательская работа
- 17. ПРЯМОУГОЛЬНИКПрямоугольником называется параллелограмм, у которого все углы прямые
- 18. Практическая работа №1.Прямоугольник.1. измерить диагонали, 2.данные занести в таблицу №13. сделать выводы.АВСD
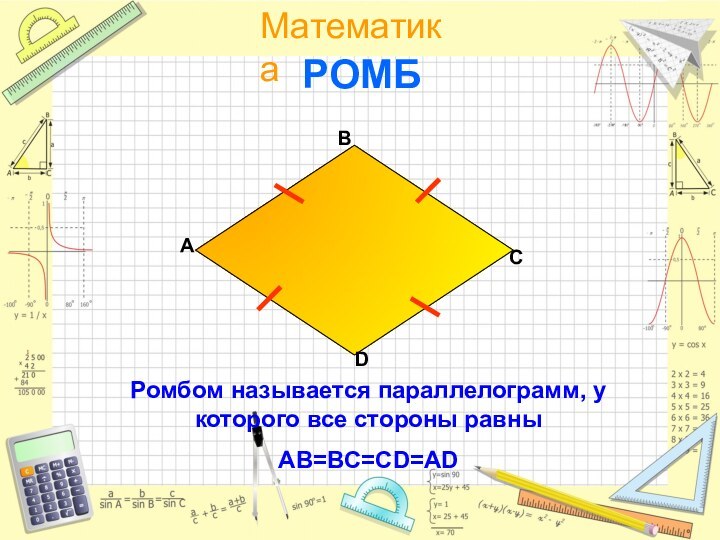
- 19. РОМБРомбом называется параллелограмм, у которого все стороны равныAB=BC=CD=ADADCB
- 20. Практическая работа №21.Измерить углы:
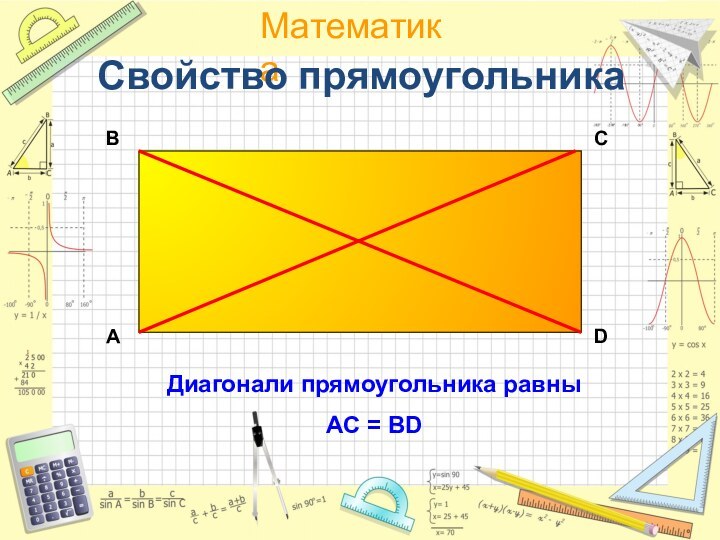
- 21. Диагонали прямоугольника равныAC = BDАDCBСвойство прямоугольника
- 22. Дано: ABCD - прямоугольник,АС и DВ
- 23. ОВАСDДано: ABCD - прямоугольник,АВ = 3см, AD=
- 24. Диагонали ромба являются биссектрисами его углов
- 25. Теорема: Диагонали ромба пересекаются
- 26. Дано:ABCD- ромб,
- 27. КвадратКвадратом называется прямоугольник, у которого все стороны равныAB = BC = CD = ADАDСВ
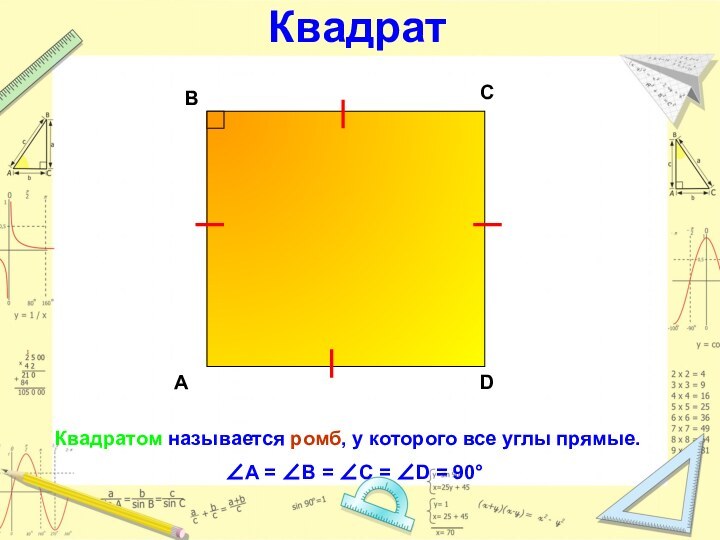
- 28. КвадратКвадратом называется ромб, у которого все углы прямые.A = B = C = D = 90°АDСВ
- 29. OAB = CD BC = ADAB || CD BC || ADAO = OC BO = OD
- 30. Ромбдиагонали которого в точке пересечения делятся пополампара
- 32. Домашнее задание1. выучить определения и свойства п.45,462.№403,405.
- 34. Скачать презентацию
- 35. Похожие презентации


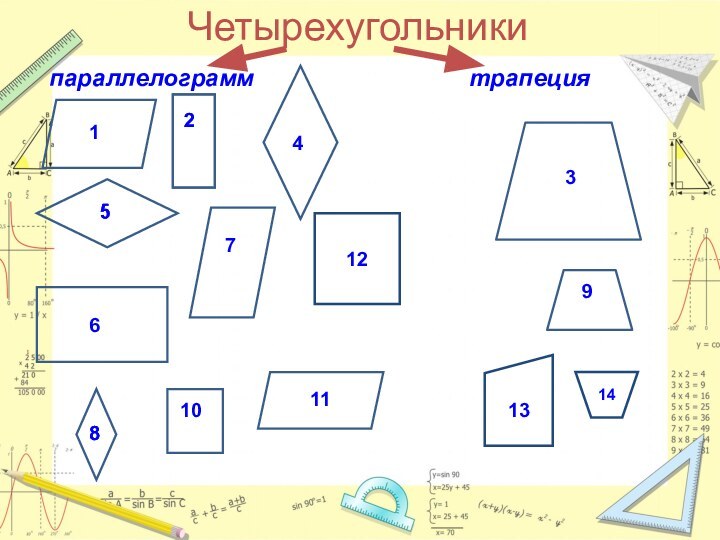









Слайд 2 Одной из основных и простейших фигур в геометрии
является четырехугольник.
четырехугольник, что иногда говорят о «геометрии четырехугольника» как о самостоятельном разделе геометрии.
Слайд 3
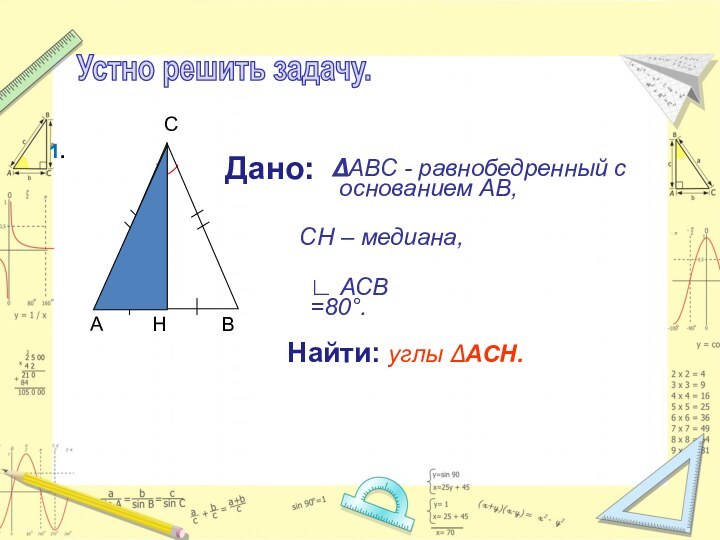
Дано:
Найти: углы ∆ACH.
1.
∆ABC - равнобедренный с
основанием
AB,
CH – медиана,
∟ АСВ =80°.
Устно решить задачу.
Слайд 4
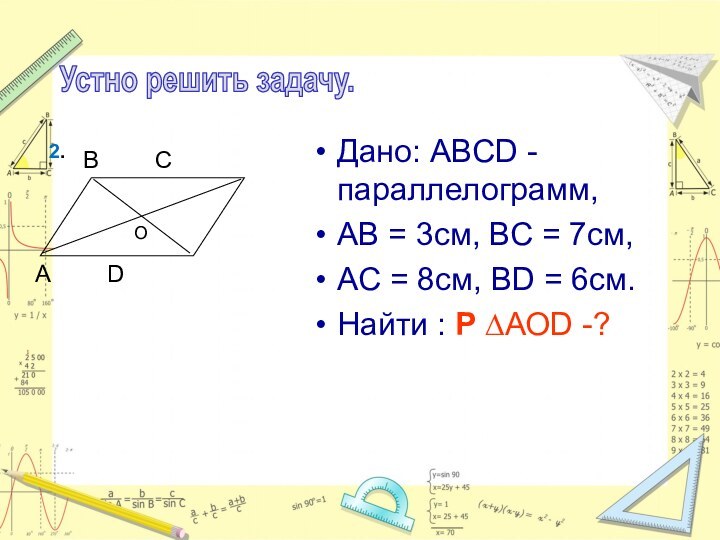
2.
Устно решить задачу.
Дано: ABCD - параллелограмм,
AB = 3см,
ВС = 7см,
АС = 8см, ВD = 6см.
Найти :
Р ∆АОD -?О
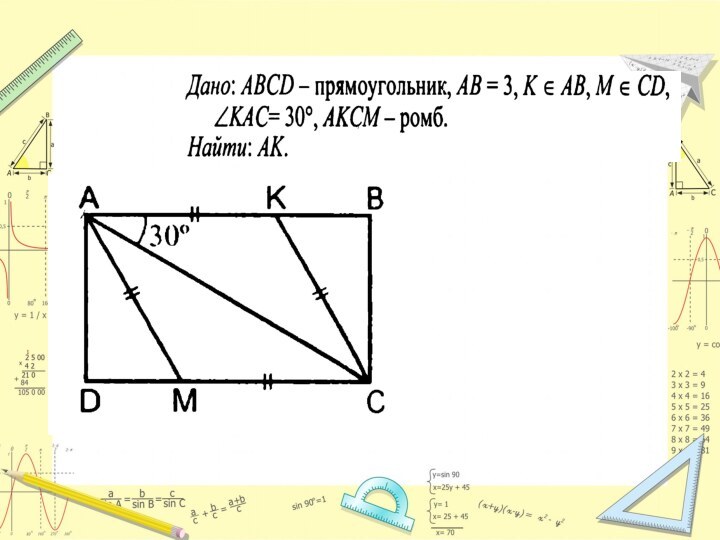
Слайд 12
О
В
А
С
D
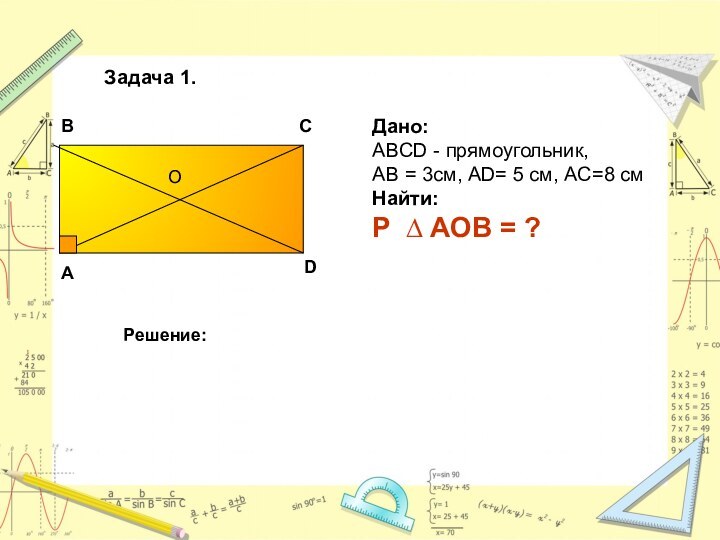
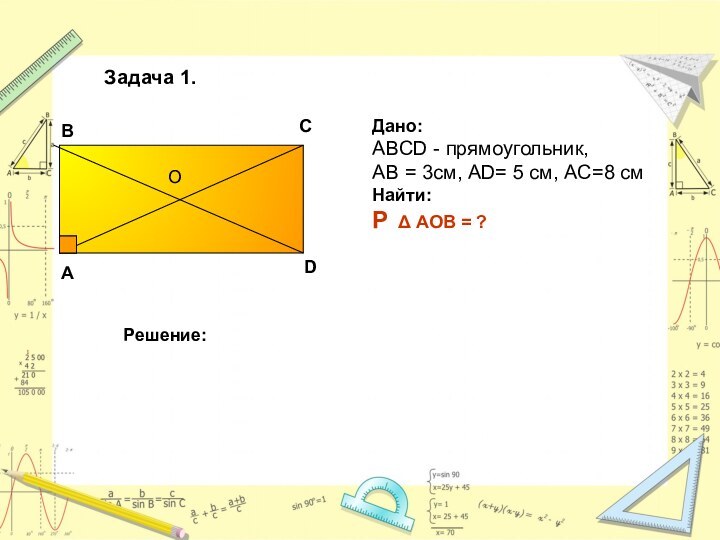
Дано:
ABCD - прямоугольник,
АВ = 3см, AD= 5
см, AC=8 см
Найти:
P ∆ AOB = ?
Решение:
Задача 1.
Слайд 15
Цели урока:
дать определение,
и установить свойства и
признаки:
прямоугольника, ромба, квадрата.
Слайд 16
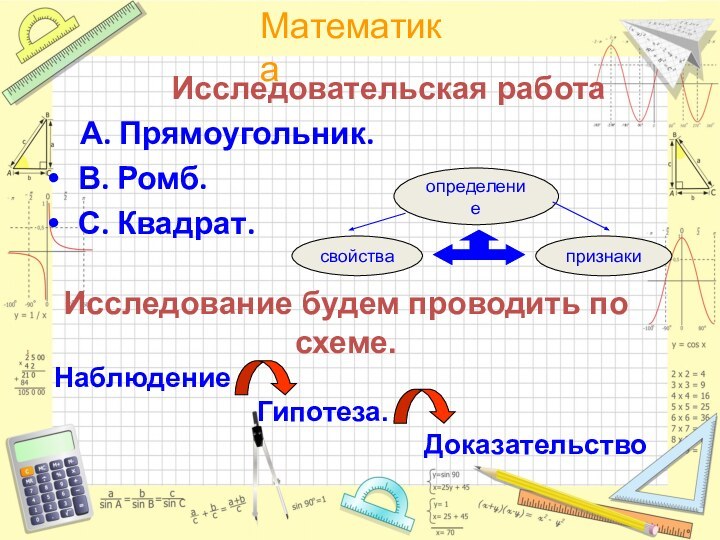
Исследовательская работа
А. Прямоугольник.
В. Ромб.
С.
Квадрат.Исследование будем проводить по схеме.
Наблюдение
Гипотеза.
Доказательство
определение
свойства
признаки
Слайд 18
Практическая работа №1.
Прямоугольник.
1. измерить диагонали,
2.данные занести в
таблицу №1
3. сделать выводы.
А
В
С
D
Слайд 20
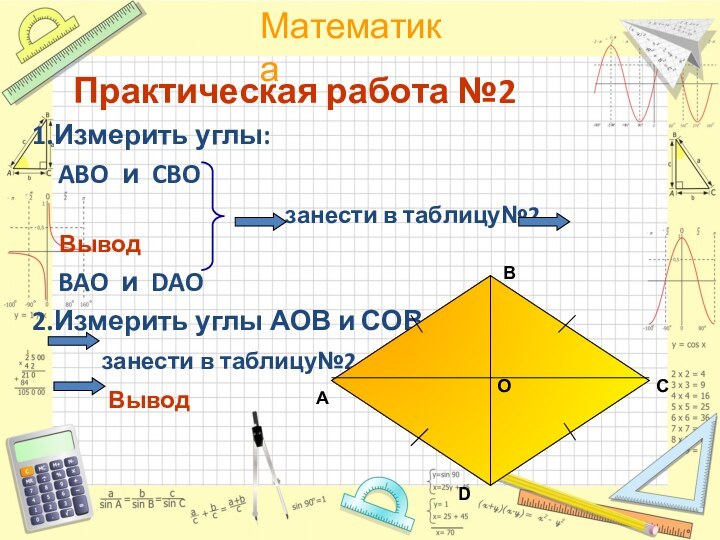
Практическая работа №2
1.Измерить углы:
ABO и CBO
занести в таблицу№2 ВыводBAO и DAO
2.Измерить углы АОВ и СОВ
занести в таблицу№2
Вывод
А
В
С
D
O
Слайд 22
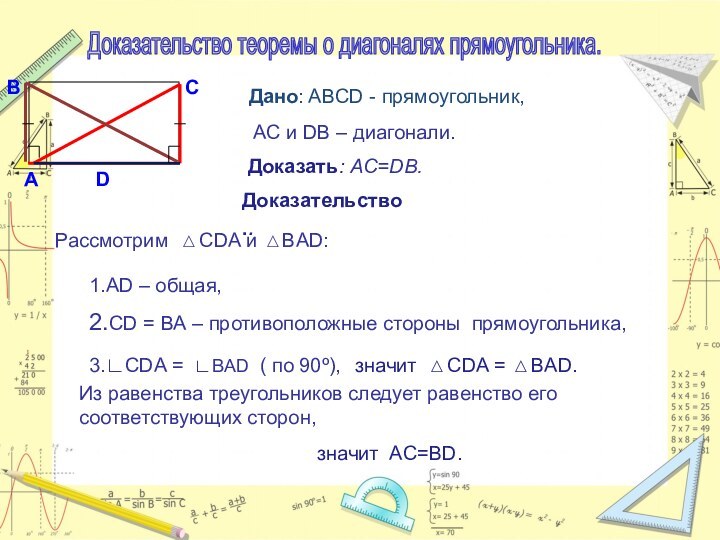
Дано: ABCD - прямоугольник,
АС и DВ –
диагонали.
Доказать: AC=DВ.
Доказательство..
Рассмотрим CDA и BAD:
1.AD – общая,
2.CD =
ВА – противоположные стороны прямоугольника, 3.∟СDA = ∟BAD ( по 90º),
значит CDA = BAD.
Из равенства треугольников следует равенство его соответствующих сторон,
значит AC=BD.
Доказательство теоремы о диагоналях прямоугольника.
С
В
Слайд 23
О
В
А
С
D
Дано:
ABCD - прямоугольник,
АВ = 3см, AD= 5
см, AC=8 см
Найти:
P Δ AOB = ?
Решение:
Задача 1.
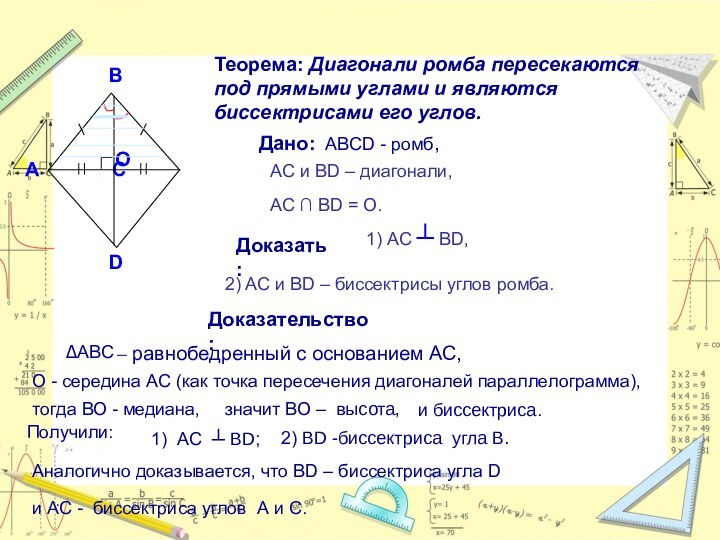
Слайд 25 Теорема: Диагонали ромба пересекаются
под прямыми углами и являются биссектрисами его углов.
Дано: АBCD - ромб,
AC и BD – диагонали,
АС ∩ BD = O.
O
Доказать:
1) АС ┴ BD,
2) AC и BD – биссектрисы углов ромба.
Доказательство:
∆АВС
О - середина АС (как точка пересечения диагоналей параллелограмма),
тогда ВО - медиана,
значит ВО – высота,
1) АС ┴ BD;
Получили:
Аналогично доказывается, что BD – биссектриса угла D
и АС - биссектриса углов А и С.
2) BD -биссектриса угла В.
и биссектриса.
.
– равнобедренный с основанием АС,
Слайд 27
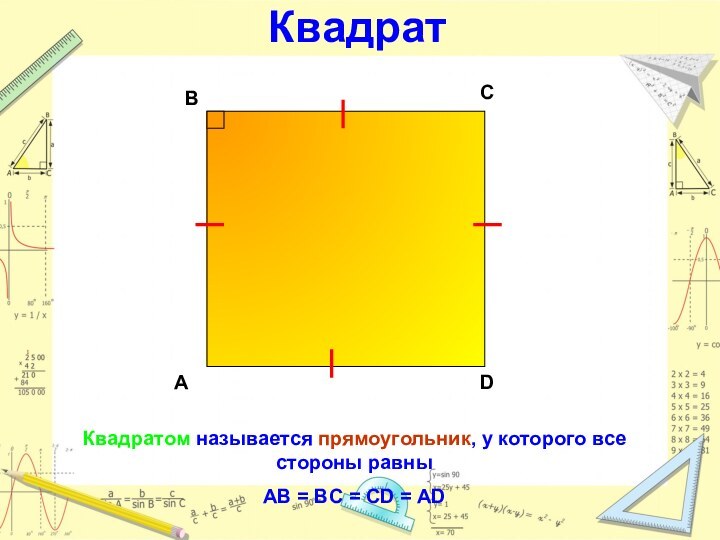
Квадрат
Квадратом называется прямоугольник, у которого все стороны равны
AB
= BC = CD = AD
А
D
С
В
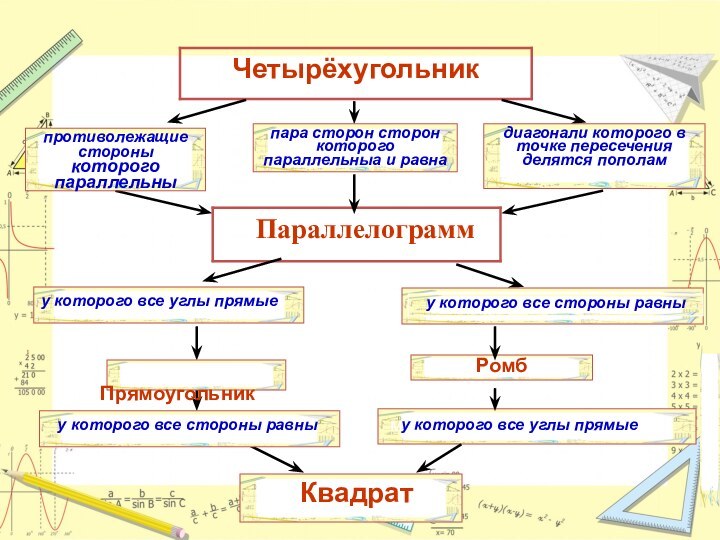
Слайд 30
Ромб
диагонали которого в точке пересечения делятся пополам
пара сторон
сторон которого параллельныа и равна
противолежащие стороны которого параллельны
у
которого все углы прямые Прямоугольник
у которого все стороны равны





























