Презентация на тему Разбор заданий 12 на клетчатой бумаге. ГИА-2014 математика

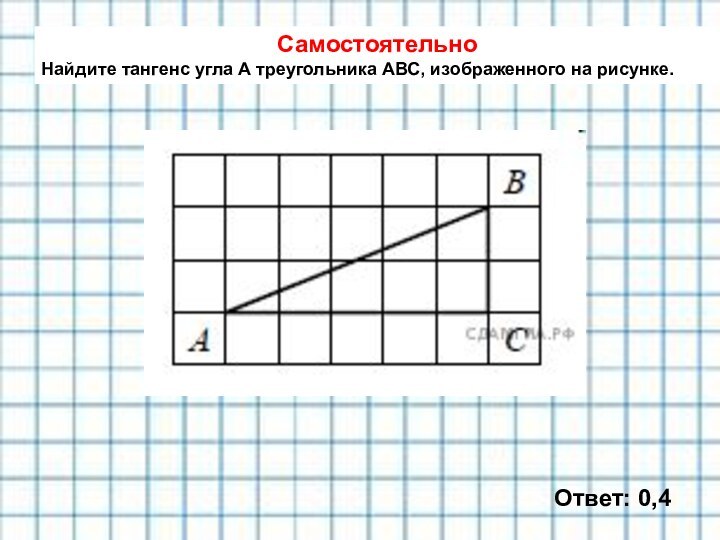
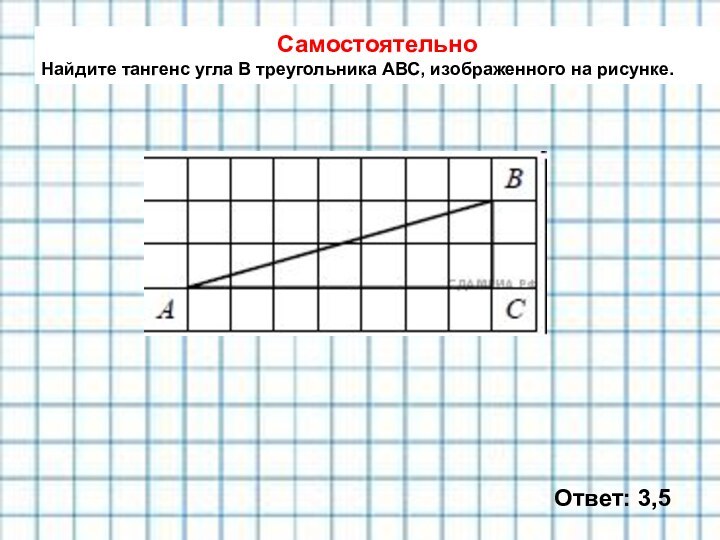
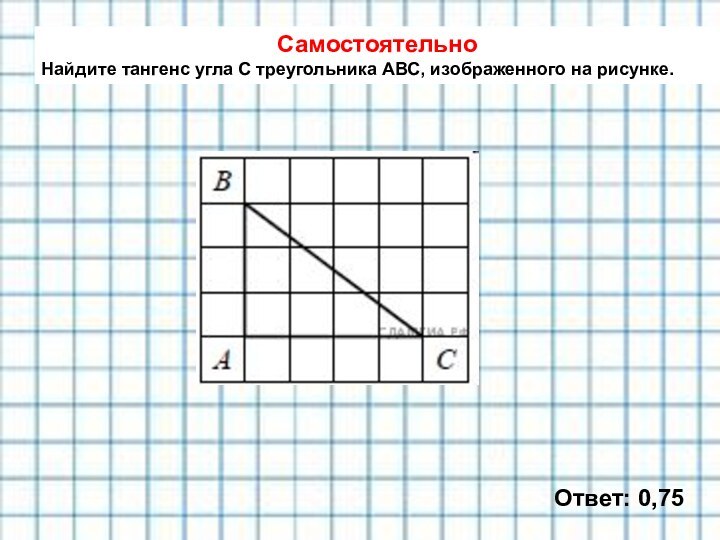
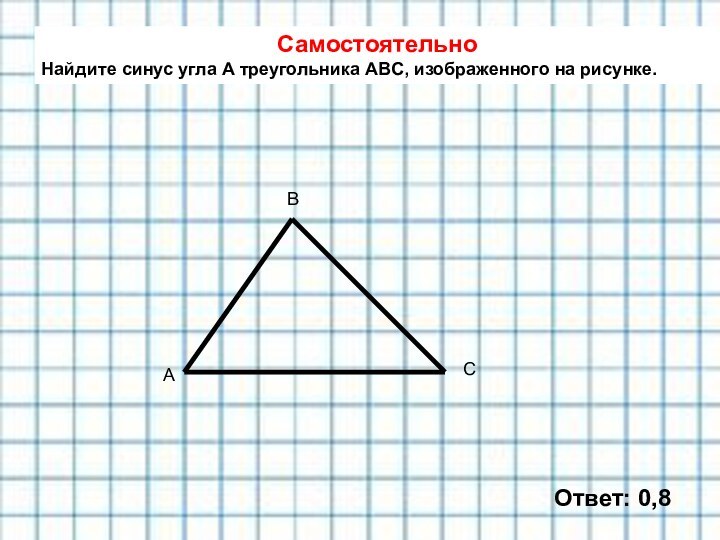
с размером клетки
1 см х 1 см. Ответ

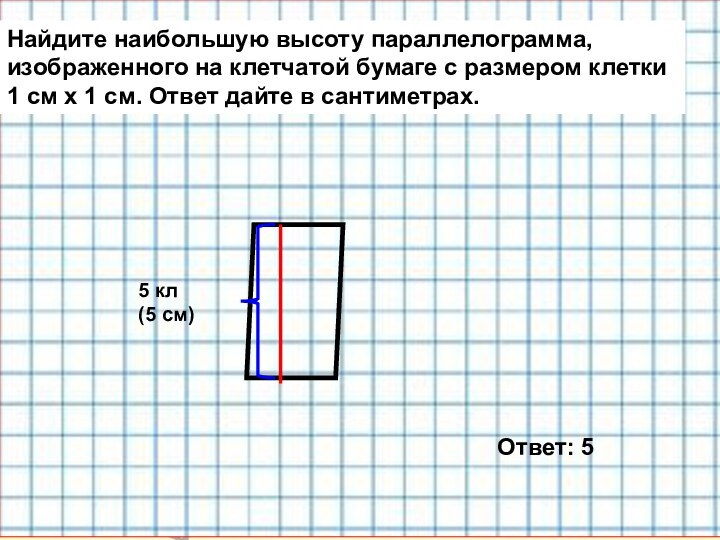
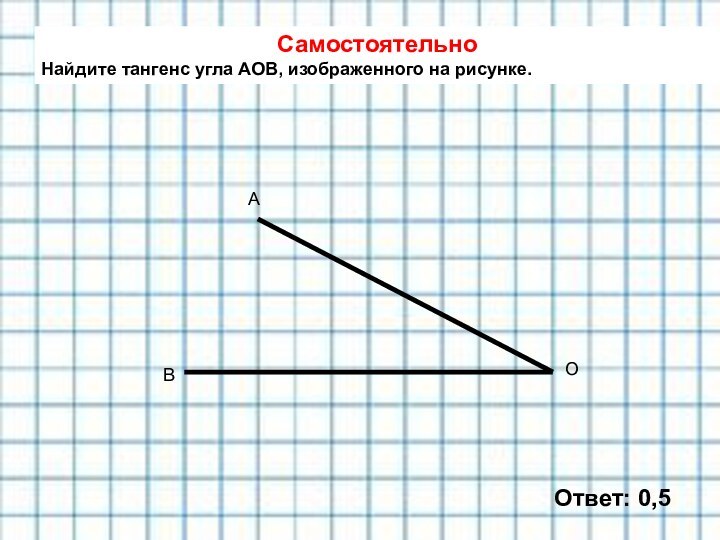
Найдите наибольшую высоту параллелограмма,
изображенного на клетчатой бумаге с размером клетки
1 см х 1 см. Ответ дайте в сантиметрах.

5 кл
(5 см)

Ответ: 5

с размером клетки
1 см х 1 см. Ответ

Проверка

2

Ответ: 2

с размером клетки
1 см х 1 см. Ответ

Найдите среднюю линию трапеции,
изображенной на клетчатой бумаге с размером клетки
1 см х 1 см. Ответ дайте в сантиметрах.

Средняя линия трапеции параллельна основаниям
и равна их полусумме

основания

основания

Средняя
линия

2

4

Ср.линия =

(2+4)/2=3

Ответ: 3

с размером клетки
1 см х 1 см. Ответ

1

4

Ср.линия = (1+4)/2=5/2=2,5

Ответ: 2,5

Проверка

острого угла прямоугольного треугольника называется
отношение противолежащего катета к

А

В

С

sinA =

3

0,6

Ответ: 0,6

острого угла прямоугольного треугольника называется
отношение противолежащего катета к

1

5

Ответ: 0,2

- тупой
cos(1800 - β) = - cosβ
β
cosα = cos(1800

∠β - острый

Косинусом острого угла прямоугольного треугольника называется
отношение прилежащего катета к гипотенузе.

3

4

cosβ =

a

cosα = - cosβ = - 0,6

Ответ: -0,6

- α) = - cosα

рисунке.
Ответ: 0,4

рисунке.
Ответ: 3,5

рисунке.
Ответ: 0,75

рисунке.
Ответ: 0,8
А
С
В