- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Разложение на простые множители
Содержание
- 2. Цели урока Познакомить учащихся с разложением на
- 3. Вычислить устно:1,4+5,6 :2
- 4. Из истории математикиИзучением свойств простых чиселЗанимался русский
- 5. Изучение нового материалаЗадача: Нужно выделить участок земли
- 6. Решение задачи:1) 18 = 1 *182) 18
- 7. Решая задачу , мы число 18 представили
- 8. Определения. Разложить ( натуральное) число на простые
- 9. Разложение на простые множителиВсякое составное число может
- 10. Разложение на простые множители Перебираем числа по
- 11. Закрепление изученногоУстно:разложить простые на множители:16, 15,
- 12. Самостоятельная работа Разложить на простые множителиВариант 1Вариант 2.1) 422) 2203) 4001) 542) 803) 250
- 13. 42=2 * 3 * 742 221
- 14. Скачать презентацию
- 15. Похожие презентации
Цели урока Познакомить учащихся с разложением на простые множители числа;повторить признаки делимости чисел и научить использовать их при разложении чисел на простые множители.












Слайд 2
Цели урока
Познакомить учащихся с разложением на простые
множители числа;
при разложении чисел на простые множители.
Слайд 3
Вычислить устно:
1,4+5,6
:2
-
1.7
: 0,3
*0,1
1: 4+0,05
*7
+3,4
: 5
4- 3,4
*1.4
+0.06
:1.8
*3
?
?
?
Слайд 4
Из истории математики
Изучением свойств простых чисел
Занимался русский математик
Пафнутий Львович Чебышев доказал, что между любыми натуральными числами
,большим 1 , и числом, вдвое большим, всегда имеется не менее одного простого числа.
Слайд 5
Изучение нового материала
Задача: Нужно выделить участок земли прямоугольной
формы площадью 18 квадратных метров.Какими могут быть размеры этого
участка , если они должны выражаться натуральными числами ?
Слайд 6
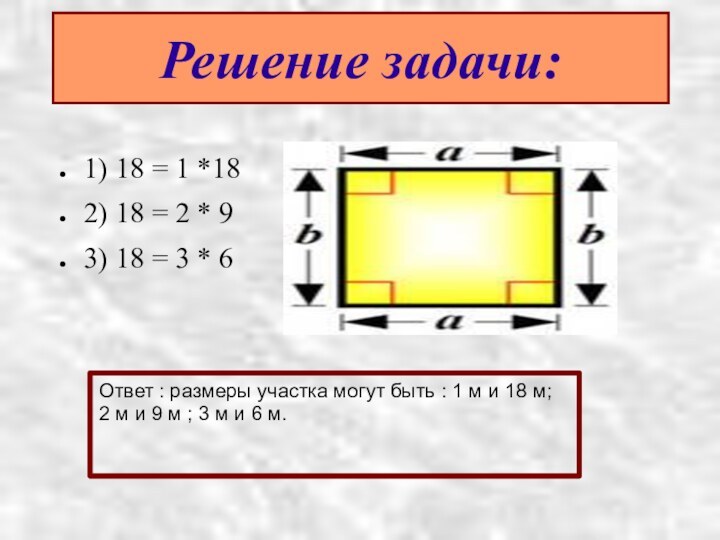
Решение задачи:
1) 18 = 1 *18
2) 18 =
2 * 9
3) 18 = 3 * 6
Ответ :
размеры участка могут быть : 1 м и 18 м; 2 м и 9 м ; 3 м и 6 м.
Слайд 7 Решая задачу , мы число 18 представили в
виде произведения натуральных чисел
.Говорят : разложили на множители .
Если в разложении , например , числа 18 = 3 *6 составной множитель 6 представить в виде произведения двух Простых множителей 2 и 3 , то тогда число 18 будет разложено на простые множители : 18 = 3 * 6 = 3* 2 * 3.
Обычно записывают в порядке возрастания :
18 = 2 * 3 * 3
Слайд 8
Определения.
Разложить ( натуральное) число на простые множители
— значит , представить это число в виде произведения
Продолжить
3276
= 2 * 2 * 3*3 * 7* 133276
1638
819
273
91
13
1
2
2
3
3
7
13
При разложении числа на простые множители
произведение одинаковых множителей
представляют в виде степени :
3276=
Слайд 9
Разложение на простые множители
Всякое составное число может быть
единственным образомпредставлено в виде произведения простых множителей. Например,
48
= 2 · 2 · 2 · 2 · 3, 225 = 3 · 3 · 5 · 5, 1050 = 2 · 3 · 5 · 5 · 7 .Для небольших чисел это разложение легко делается на основе таблицы умножения. Для больших чисел рекомендуем пользоваться следующим способом, который рассмотрим на конкретном примере. Разложим на простые множители число 1463. Для этого воспользуемся таблицей простых чисел:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,
47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101,
103, 107, 109, 113, 127, 131, 137, 139, 149, 151,
157, 163, 167, 173, 179, 181, 191, 193, 197, 199.
Слайд 10
Разложение на простые множители
Перебираем числа по этой
таблице и останавливаемся на том числе, которое является делителем
данного числа. В нашем примере это 7. Делим 1463 на 7 и получаем 209. Теперь повторяем процесс перебора простых чисел для 209 и останавливаемся на числе 11, которое является его делителем (см. параграф “Признаки делимости”). Делим 209 на 11 и получаем 19, которое в соответствии с этой же таблицей является простым числом. Таким образом, имеем: 1463 = 7 ∙ 11 ∙ 19, т.е. простыми делителями числа 1463 являются 7, 11 и 19.
Слайд 11
Закрепление изученного
Устно:разложить простые на множители:
16, 15, 20;
72 ;150; 25; 36
Выполнить письменно :
№ 115( а
), 116.( а), 118 ( А , Б )Повторение : 122, 126 ( а , б, в)
Слайд 12
Самостоятельная работа
Разложить на простые множители
Вариант 1
Вариант 2.
1)
42
2) 220
3) 400
1) 54
2) 80
3) 250
Слайд 13
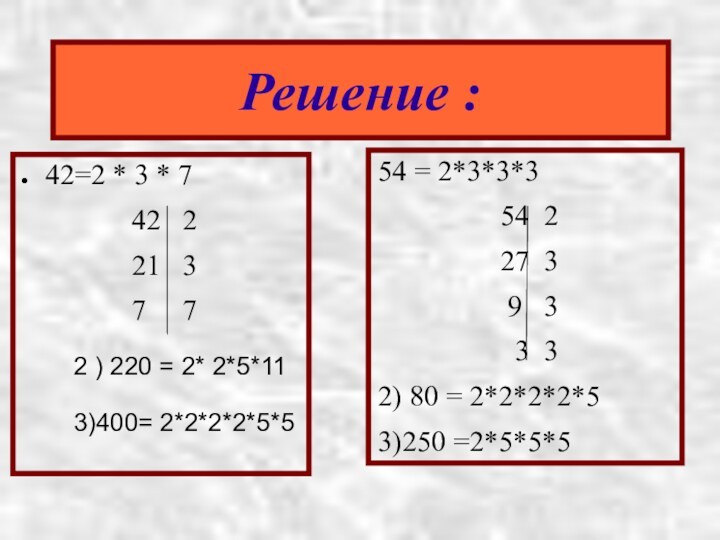
42=2 * 3 * 7
42 2
21
3
7 7
54 = 2*3*3*3
54 2
27 3
9
33 3
2) 80 = 2*2*2*2*5
3)250 =2*5*5*5
Решение :
2 ) 220 = 2* 2*5*11
3)400= 2*2*2*2*5*5