- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение ЕГЭ по математике
Содержание
- 2. Функция үзлекләрен тигезләмәләр һәмтигезссезлекләр чишүдә куллану .МОУ «Староузюмское СОШ»Математика укытучысы: Ситтигуллина Әлфия БорисовнаЕГЭ га хәзерлек
- 3. Применим для задач в которых множества значений
- 4. удовлетворяет второму уравнению.Решение. Оценим обе части уравнения.
- 5. Пример 2. Решить уравнение Решение: Оценим обе
- 6. Сделаем оценку функций, входящих в неравенство.Пример 3.
- 7. Пример 5. Решить уравнение 2) Решая первое
- 8. Пример 9. Решить уравнение Решение:
- 9. Пример 10. Доказать, что уравнение не имеет
- 10. ИСПОЛЬЗОВАНИЕ ОБЛАСТИ ОПРЕДЕЛЕНИЯ ФУНКЦИИ Итак, единственной точкой,
- 11. Решить уравнение 1) Выпишем, условие существования функции,
- 12. Скачать презентацию
- 13. Похожие презентации










Слайд 3 Применим для задач в которых множества значений левой
и правой частей уравнения или неравенства имеют единственную общую
точку, являющуюся наибольшим значением для одной части и наименьшим для другой. Эту ситуацию хорошо иллюстрирует график.Как начинать решать такие задачи?
Привести уравнение или неравенство к виду
Слайд 4
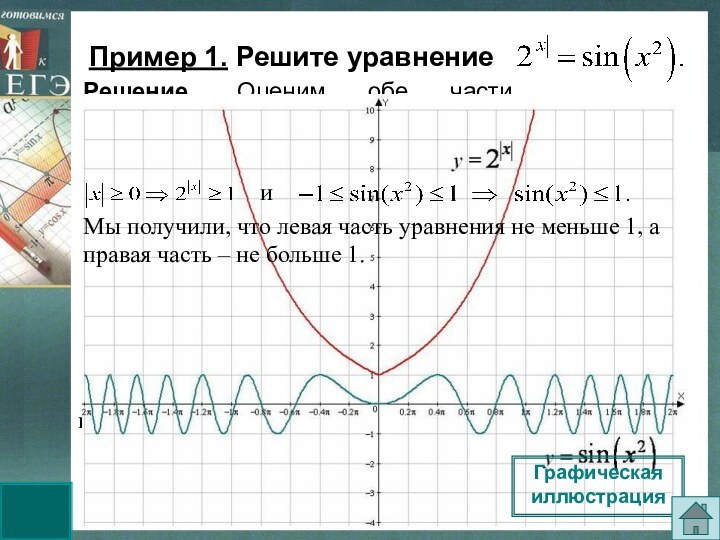
удовлетворяет второму уравнению.
Решение. Оценим обе части уравнения.
При
всех значениях х верны неравенства:
Следовательно, данное уравнение равносильно
системе: Графическая иллюстрация
Мы получили, что левая часть уравнения не меньше 1, а правая часть – не больше 1.
Слайд 5
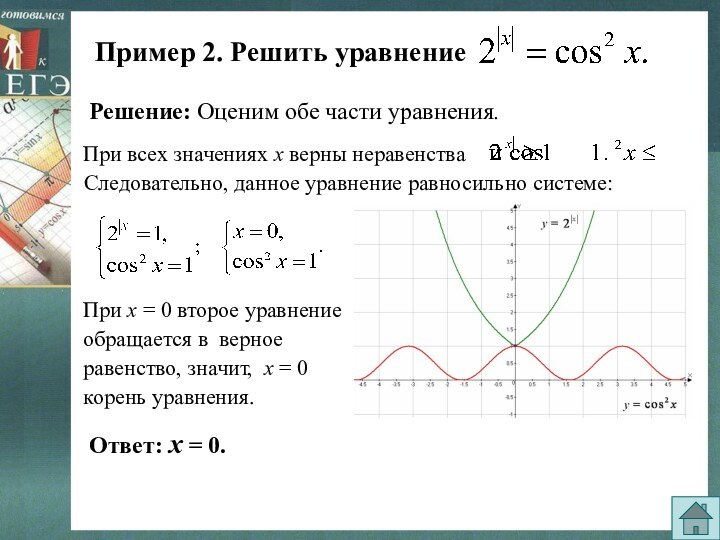
Пример 2. Решить уравнение
Решение: Оценим обе части
уравнения.
Следовательно, данное уравнение равносильно системе:
При х = 0 второе
уравнение обращается в верное равенство, значит, х = 0 корень уравнения.Ответ: х = 0.
Слайд 6
Сделаем оценку функций, входящих в неравенство.
Пример 3. Решить
неравенство
Следовательно, исходное неравенство выполняется тогда и только тогда,
когда оба множителя равны 1 одновременно. Ответ: - 1.
Решение.
Получаем х = -1 – единственное решение системы уравнений, а, значит, и данного неравенства.
Слайд 7
Пример 5. Решить уравнение
2) Решая первое уравнение
системы, находим :
3) Подставим найденные значения во второе
уравнение: Решение. Оценим обе части уравнения.
1) Каждое слагаемое левой части уравнения не больше 1, следовательно их сумма будет равна 2, если они принимают своё наибольшее значение.
Слайд 8
Пример 9. Решить уравнение
Решение:
Заметим,
что х = 1 , является корнем данного уравнения.
Левая часть уравнения представляет собой сумму двух возрастающих функций и, следовательно, сама является возрастающей функцией, принимающей каждое своё значение ровно один раз.Поэтому других корней данное уравнение не имеет.
Ответ: 1.
Слайд 9
Пример 10. Доказать, что уравнение не имеет решений:
Арифметический
корень не может быть отрицательным числом, поэтому уравнение решений
не имеет.?
?
?
?
?
Слайд 10
ИСПОЛЬЗОВАНИЕ ОБЛАСТИ
ОПРЕДЕЛЕНИЯ ФУНКЦИИ
Итак, единственной точкой, в
которой определены эти радикалы, является x = 1. Легко проверить, что
это число – корень уравнения.Решить уравнение:
Решение.
Второй радикал определен при любых значениях х.
Выражение под третьим радикалом неотрицательно если
Ответ: 1.
Слайд 11
Решить уравнение
1) Выпишем, условие существования функции, стоящей
в левой части:
Решить данное неравенство довольно сложно.
3)
Значит, исходное уравнение тоже не имеет решений, так как левая часть его – неотрицательная функция!Ответ: .
Решение.
2) Проверим не отрицательность правой части:
Последнее неравенство решений не имеет.