Презентация на тему Математические предложения

10. Это равенство»
37 + 6  37
20 + 8

 20
«некоторые числа делятся на 5»
5 + x = 9

Определим истинны ли они или ложные
Предложения 1,2,4 – истинные
Предложение 3 – ложное
Предложение 5 – нельзя указать истинное оно или ложное

высказывания

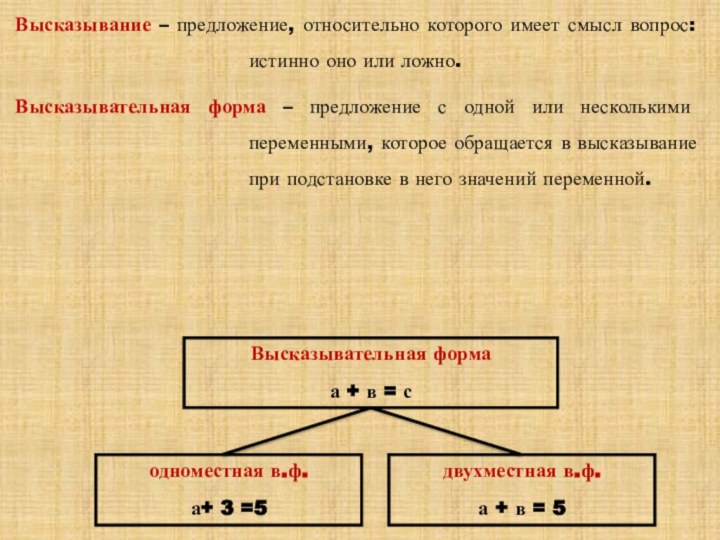
Высказывательная форма

истинно оно или ложно.
Высказывательная форма – предложение с одной

или несколькими переменными, которое обращается в высказывание при подстановке в него значений переменной.

истинно
В – «Л» - высказывание В – ложно
«И», «Л»

- значения истинности высказывания
Множество истинности высказывательной формы – это значения переменной, которые обращают высказывательную форму в истинное высказывание.
Пример: определить множество истинности высказывательной формы x  6, если а) x  N
б) x  Z в) x R
Множество истинности – {1,2,3,4,5}
Множество истинности – {0,1,2,3,4,5}
Множество истинности – {- ; 6}

двух простых предложений можно составить новые предложения с помощью

союзов «и», «или»…
Логическая связка – «и», «или», «если,…то», «не», «тогда и только тогда, когда».
Составные предложения – это предложения, образованные из элементарных с помощью логических связок.

каких элементарных предложений оно образовано;
С помощью, каких логических связок

оно образовано.
Пример: 1) x ≥7 – это составная высказывательная форма.
Логическая структура: «А или В»
Элементарные высказывательные формы – А – «x  7»
В - «x = 7»
Логическая связка – «или»

в нем равны» - это составное высказывание.
Логическая структура: «Если

А, то В»
Элементарные предложения:
А – «треугольник равнобедренный»
В – «углы при основании равны»
Логические связки: «Если ……, то».

– «А и В»
Элементарные высказывательные формы –
А –

«25 – четное число»
В – «25 – делится на 5»
Логическая связка – « и »
Проблема: «Как определить значение истинности составных предложений?»
Составное высказывание вида «А и В» называют конъюнкцией (лат. «соединение»), обозначают А  В.

А  В, которое истинно, когда оба высказывания истинны,

и ложно, когда хотя бы одно из высказываний ложно.
Пример: А – «Л»  А В – «Л» (по определению)
В – «И»
Составные высказывания вида «А или В» называют дизъюнкцией (лат. «разделение»), обозначают АВ.

А  В, которое истинно, когда истинно хотя бы

одно из высказываний, и ложно, когда оба высказывания ложны.
Пример: «Число 25 делится на 5 или на 3».
А – «25 делится на 5»
В – «25 делится на 3»
Логическая связка – или
Логическая структура - АВ
А – «И»  – АВ «И» (по определению)
В – «Л»

А(х)  В(х) обращается в истинное высказывание, если обращаются

в истинное высказывание обе высказывательные формы А(х) и В(х) при значениях х из области определения Х.
Пример: х + 3 13 А(х) – х+313
3х 15 В(х) – 3х  15
Логическая структура А(х)  В(х)
х  10
х  5

Ответ: А(х)  В(х) – «И» при х  (5;10).

обращается в истинное высказывание, при тех значениях х из

области определения Х, при которых обращается в истинное высказывание хотя бы одна из высказывательных форм.
Пример: (х + 7) (х - 4) = 0
Произведение равно нулю, когда один из множителей равен нулю.
А(х) – х + 7=0
В(х) – х – 4 =0
Логическая структура: А(х)  В(х)
х +7=0 или х – 4 =0
х = - 7 х=4

Ответ. А(х)  В(х) - И при х  (-7;4).

«есть», «хотя бы один».
Обозначение:  х – «существует х»
(

х) Ах – «существует такое значение х, что А(х) – истинное высказывание».
Истинность высказывания с квантором существования устанавливается при помощи конкретного примера, а ложность - доказывается.

существования – «некоторые» и оно – «Л». Это необходимо

доказать.
В равностороннем треугольнике все углы по 60, а в прямоугольном один из углов - 90. Следовательно, ни один прямоугольный треугольник не может быть равносторонним.

и «все».
Обозначение: х – для всякого х.
(х) А(х) –

«для всякого х предложения А(х) – истинное высказывание».
Истинность высказывания с квантором общности устанавливается путем доказательства, а ложность – контрпример.
 Пример: «Всякое натуральное число делится на 2 » высказывание содержит квантор общности – «всякое и оно – Л, т.к. «3 не делится на 2» - контрпример.

что – либо отрицается.
Пример: «15 – простое число» А

– Л
Построим отрицание высказывания: «неверно, что 15 простое число» - И
Обозначение: Ā
Читают: «Не А» или «Неверно, что А».

ложно, если высказывание А истинно, и истинно, если высказывание

А- ложно.

конъюнкции (дизъюнкции), достаточно заменить отрицаниями составляющие её высказывания, а

союз «и» («или») заменить союзом «или» («и»).
 Пример: «Число 15 – нечетное и делится на 5».
Построить отрицание высказывания.
Решение
А  В – И

построить двумя способами:
перед высказыванием ставится слова «неверно что»;
квантор общности

(существования) заменяется квантором существования (общности), а предложение, стоящее после квантора заменяется его отрицанием.

- Л – высказывание с квантором общности.
способ. Ā –

«Неверно, что всякий многоугольник является четырехугольником» - И
А – Л  Ā построено верно
Ā – И
способ. Ā - «Некоторые многоугольники не являются четырехугольниками» - И
А – Л  Ā построено верно
Ā – И

И – высказывание с квантором существования.
способ. Ā - «Неверно,

что некоторые свойства квадрата присущи прямоугольнику».
А – И  Ā построен верно
Ā – Л
способ. Ā - «Всякое свойство квадрата не присуще прямоугольнику» - Л
А – И
Ā– Л

5»
В (х) – «х 2»



Как связаны между собой?
Можно

утверждать:
«Все числа больше пяти больше двух» или
«из того, что х 5 следует, что х 2 ».

S формы А (х), если В (х) обращается в

истинное высказывание при всех тех значениях х, при которых А (х) истинна.
Обозначение: А(х)В(х)
Читают:
Из А(х) следует В;
Всякое А(х) есть В(х);
Если А (х), то В(х);
В(х)есть следствие А(х);
А(х) – достаточное условие для В (х)
В(х) – необходимое условие для А(х)
Как установить истинность предложения А(х)В(х)?
Его можно сформулировать в виде:
«Всякое А(х) есть В(х)»

устанавливается путем доказательства, а ложность – контрпример.
Рассмотрим высказывания:
А(х) –

«треугольник равнобедренный»
В(х) – «Углы при основании треугольника равны »
А(х) В (х) – И
«Если в треугольнике углы при основании равны, то он равнобедренный» - И
Говорят: предложения А(х) и В(х) – равносильны.

предложения А(х) следует предложения В(х), а из предложения В(х)

следует предложение А(х).
Обозначение: А(х)В(х)
Читают:
А(х) равносильно В(х)
А(х) тогда и только тогда, когда В(х)
А(х) – необходимое и достаточное условие В(х)
В(х) – необходимое и достаточное условие А(х)

формой.
Как определить логическую структуру составного предложения?
Сформулируйте различие между конъюнкцией

и дизъюнкцией.
Как определяется истинность конъюнкции и дизъюнкции высказываний и высказывательных форм?
Сформулируйте правила определения истинности высказываний с кванторами.
Где используется закон де Моргана?
Каким образом можно построить отрицание высказываний с кванторами?
В каких случаях используют отношение логического следования и равносильности между предложениями?
В чем отличие теоремы от правила?
Какова логическая структура различных видов теорем?
Каким законом связаны различные виды теорем?