и применению графиков при их решении
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть







Ответ: ( -∞; +∞).
б) у =
Ответ: (-∞; -3) U (-3; 2) U (2; +∞).
в) у =
Ответ: (-∞; -3] U [3; +∞).
Задание 2. Разложите на множители многочлен х4 - 10х2 + 9.
(Указание. Воспользуйтесь формулой аt2 + вt + с =а( t - t1)( t - t2))
Ответ: (х 2 - 1)(х 2 - 9) = (x - 1)(x + 1) (x - 3)(x + 3).
Задание 3. Продолжите:
a) функция у = kx + b –
линейная,
график −
прямая,
при k > 0 функция
возрастает, при k < 0 функция
убывает ;
б) функция у = ах2 + вх + с −
квадратичная, график −
парабола,
а > 0, ветви −
вверх, а < 0, ветви –
вниз;
D > 0,
2 нуля функции;
D < 0,
нет нулей функции;
D = 0,
1 нуль функции.
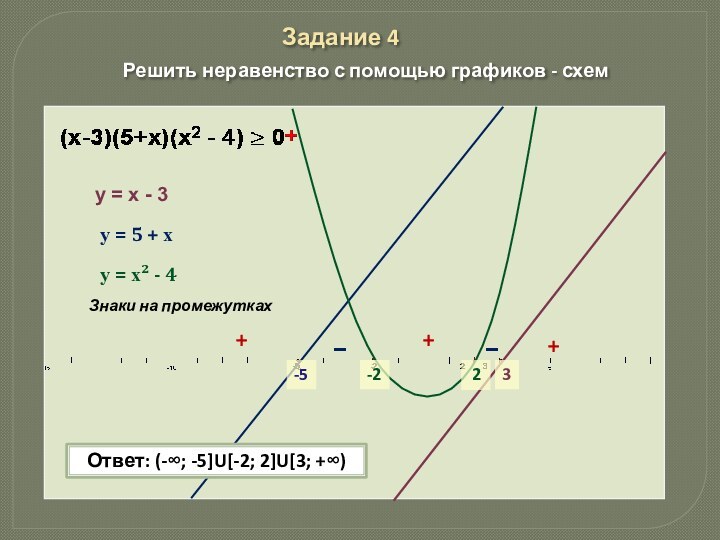
у = х² - 4
Знаки на промежутках
+
−
+
−
+
Ответ: (-∞; -5]U[-2; 2]U[3; +∞)
3
-5
2
-2
−
−
+
+
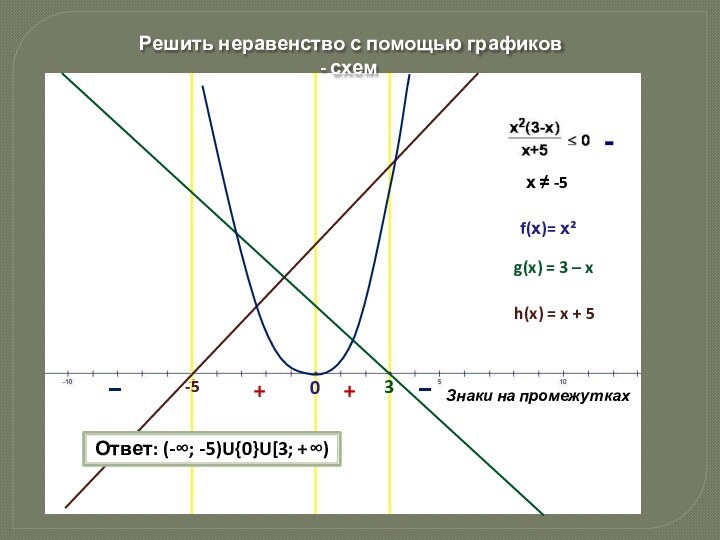
Ответ: (-∞; -5)U{0}U[3; +∞)
f(х)= х²
0
3
-5
х ≠ -5
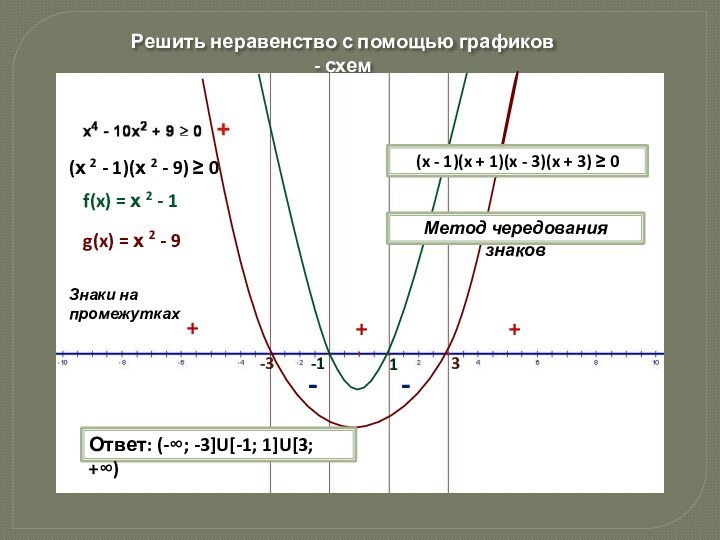
f(x) = х 2 - 1
Знаки на промежутках
+
+
+
-
Ответ: (-∞; -3]U[-1; 1]U[3; +∞)
3
-3
-1
1
(x - 1)(x + 1)(x - 3)(x + 3) ≥ 0
Метод чередования знаков
-
Ответы:
А. (0; 0,5) U (0,5; 1)
Б. [-4; 0)U(0; 4]
Д. [0,2; 0,25]U{0,4}
Е. (-∞; -8] U {-3} U {3}
O. (-∞; -6)U(-3; 3)U(3; +∞)
П. (-∞; -7)U(-3; 2)U(4; +∞)
Р. Другой ответ
Ключевое слово «ПОБЕДА»