- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение неравенств методом интервалов
Содержание
- 2. Треугольниксимволизирует лидерство. Самой характерной особенностью человека, выбравшего
- 3. КвадратОсновные качества человека, выбравшего эту фигуру –
- 4. самая доброжелательная фигура. Обладатель этого символа счастлив,
- 5. Устная работа
- 6.
- 7. Поставьте соответствие между неравенством и числовым промежутком а)х≥9; б)х≤-7; в)-7≤х
- 8. Поставьте соответствие между неравенством и числовым промежутком а)х≥9; б)х≤-7; в)-7≤х
- 9.
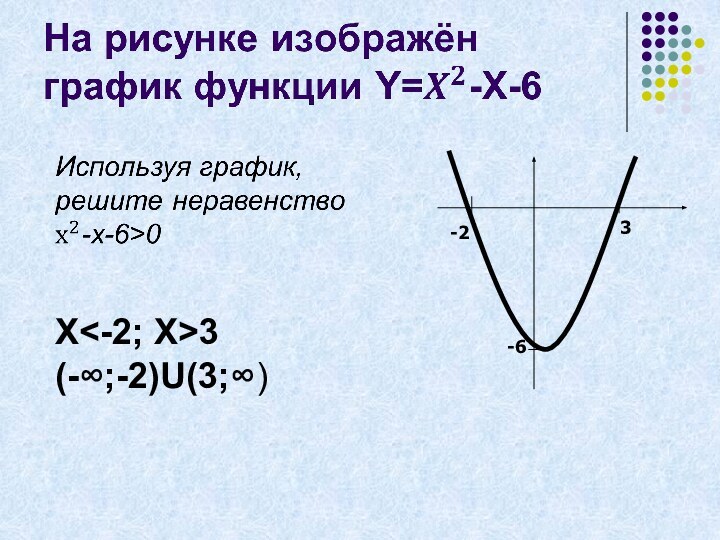
- 10. Х3 (-∞;-2)U(3;∞)
- 11. Тест1. Найти нули функции у = х2
- 12. Продолжение теста.
- 13. 8. Решением неравенства (х - 2)(х -
- 14. Проблема9 класс не умеет решать неравенства вида(х - 2)(х - 5)(х - 4) > 0
- 15. Тема: решение неравенств методом интерваловЗадача:Научиться решать неравенства методом интервалов.
- 16. Алгоритм решения неравенств методом интерваловНайти нули функции.Отметить
- 17. НАПРИМЕР:(х - 2)(х - 5)(х - 4) > 0Нули функции:(х-2)(х-5)(х-4)=0Х=2; Х=5; Х=42452
- 19. абсциссаинтерваловформуланульфункцияХорошо!1.4.3.2.5.1. Как называется координата
- 20. Скачать презентацию
- 21. Похожие презентации
Треугольниксимволизирует лидерство. Самой характерной особенностью человека, выбравшего этот символ, является концентрироваться на главной цели. Это сильная, энергичная, неудержимая личность. «Треугольник» ставит ясные цели и старается, по возможности, их выполнить.


















Слайд 2
Треугольник
символизирует лидерство. Самой характерной особенностью человека, выбравшего этот
Слайд 3
Квадрат
Основные качества человека, выбравшего эту фигуру – трудолюбие,
усердие, потребность доводить начатое дело до конца, упорство в
достижении цели. Квадрат любит порядок: всё должно находиться на своих местах и происходить вовремя.Слайд 4 самая доброжелательная фигура. Обладатель этого символа счастлив, когда
все ладят друг с другом; круг ощущает чужую радость
и боль, как свою собственную. Это очень чувствительная и эмоциональная фигура.Круг
Слайд 7 Поставьте соответствие между неравенством и числовым промежутком а)х≥9;
б)х≤-7; в)-7≤х
3) [9;∞); 4) [-7;9); 5) (-∞;-7]Слайд 8 Поставьте соответствие между неравенством и числовым промежутком а)х≥9;
б)х≤-7; в)-7≤х
3) [9;∞); 4) [-7;9); 5) (-∞;-7]
Слайд 11
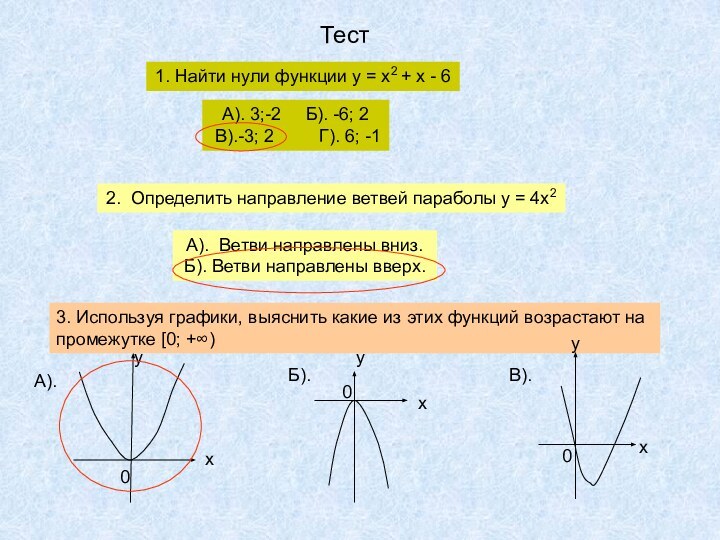
Тест
1. Найти нули функции у = х2 +
х - 6
А). 3;-2 Б). -6; 2
В).-3; 2 Г). 6; -12. Определить направление ветвей параболы у = 4х2
А). Ветви направлены вниз.
Б). Ветви направлены вверх.
3. Используя графики, выяснить какие из этих функций возрастают на
промежутке [0; +∞)
х
у
у
у
х
х
0
0
0
А).
Б).
В).
Слайд 13 8. Решением неравенства (х - 2)(х - 5)(х
- 4) > 0 является промежуток
А. (4; 5)
Б. (2; 4) и (5; + ∞) В. (- ∞; 2) и (5; + ∞) Г. (- ∞; 4) и (4;+ ∞)
Слайд 15
Тема: решение неравенств методом интервалов
Задача:
Научиться решать неравенства методом
интервалов.
Слайд 16
Алгоритм решения неравенств методом интервалов
Найти нули функции.
Отметить их
на координатном луче.
Определить знак , который имеет функция на
каждом промежутке, воспользовавшись правилом чередования знаков.Выбрать нужное множество решений данного неравенства.
Слайд 19
абсцисса
интервалов
формула
нуль
функция
Хорошо!
1.
4.
3.
2.
5.
1. Как называется
координата
точки по оси Ох?
2. Название метода решения неравенств?
3.
Один из способов задания функции. 4. Точка пересечения с осью абсцисс?
5. Переменная величина,
значение которой зависит
от изменения другой
величины.