- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение уравнений с квадратным корнем
Содержание
- 2. Способы решений полных квадратных уравнений.РазложениеВыделениеТеорема Виета«Переброска»Свойство коэффициентовГрафическое решениеВыйтиС помощью Дискриминанта
- 3. С помощью Дискриминанта.Дискриминант позволяет определить сколько же
- 4. Разложение на множители.Пример 1 х2 – 4х +
- 5. Метод выделения полного квадрата.Пример 1 х2 – 4х
- 6. Решение уравнений с использованием теоремы ВиетаПриведенное квадратное
- 7. Свободный член положительный.Если свободный член приведенного уравнения
- 8. Свободный член отрицательный.Если свободный член приведенного уравнения
- 9. Решение уравнения способом «переброски».Умножая обе части квадратного
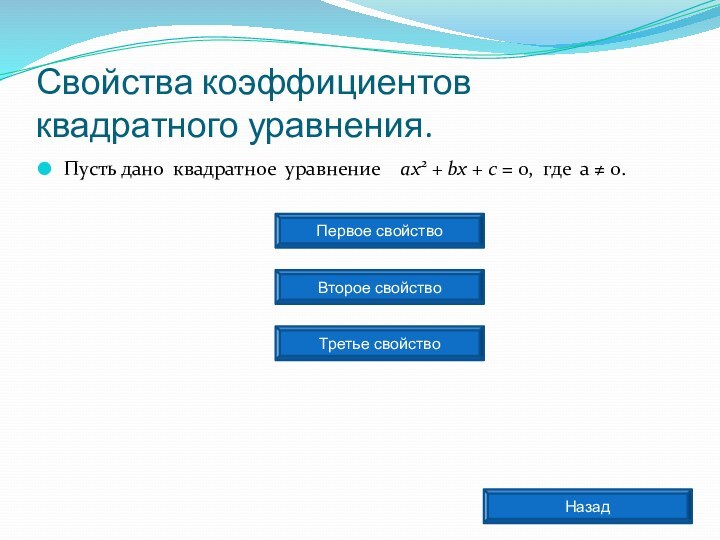
- 10. Свойства коэффициентов квадратного уравнения.Пусть дано квадратное уравнение
- 11. Первое свойство коэффициентов.Если сумма коэффициентов равна нулю,
- 12. Второе свойство коэффициентов.Если а - b +
- 13. Третье свойство коэффициентов.Если второй коэффициент b =
- 14. Графическое решение квадратных уравнений.Преобразуем уравнение х2
- 15. Примеры.Пример 1 х2 – 3х – 4 =
- 16. Приложение.Рисунок 1Рисунок 2Назад
- 17. Приложение.Рисунок 3Рисунок 4Назад
- 18. Скачать презентацию
- 19. Похожие презентации
Способы решений полных квадратных уравнений.РазложениеВыделениеТеорема Виета«Переброска»Свойство коэффициентовГрафическое решениеВыйтиС помощью Дискриминанта















Слайд 2
Способы решений полных квадратных уравнений.
Разложение
Выделение
Теорема Виета
«Переброска»
Свойство коэффициентов
Графическое решение
Выйти
С
помощью Дискриминанта
Слайд 3
С помощью Дискриминанта.
Дискриминант позволяет определить сколько же корней
имеет данное квадратное уравнение.
Формула корней квадратного уравнения имеет вид:
она позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного.
Таким образом, квадратное уравнение ах2 + bх + с = 0 ,
если D > 0, то имеет два различных корня;
если D = 0, то имеет единственный корень;
если D < 0, то не имеет корней.
Назад
Слайд 4
Разложение на множители.
Пример 1
х2 – 4х + 4
= 0, разложим левую часть уравнения на множители;
х2 – 2х – 2х + 4 = 0,
х ( х – 2 ) – 2 ( х – 2 ) = 0,
( х – 2 )( х – 2 ) = 0, произведение равно нулю, значит хотя бы один из его множителей равен нулю
х – 2 = 0,
х = 2.
Ответ: 2.
Пример 2
х2 + 10х – 24 = 0,
х2 + 12х – 2х – 24 = 0,
х ( х + 12 ) – 2 ( х + 12 ) = 0,
( х + 12 ) ( х – 2 ) = 0,
х + 12 = 0 или х – 2 = 0
х = - 12 х = 2.
Ответ: -12 и 2.
Назад
Слайд 5
Метод выделения полного квадрата.
Пример 1
х2 – 4х +
4 = 0, используем формулу сокращенного умножения;
( х – 2 )2 = 0,
х – 2 = 0,
х = 2.
Ответ: 2
Пример 2
х2 + 6х – 7 = 0, выделим в левой части полный квадрат
х2 + 2х · 3 + 32 – 32 – 7 = 0, первое слагаемое – квадрат числа х, а второе – удвоенное произведение х на 3, поэтому чтобы получить полный квадрат, нужно прибавить 32.
Преобразуем левую часть уравнения прибавляя к ней и вычитая 32.
( х + 3 )2 – 9 – 7 = 0,
( х + 3 )2 – 16 = 0,
( х + 3 )2 = 16,
х + 3 = 4 или х + 3 = - 4
х = 1 х = - 7.
Ответ: 1 и -7 .
Назад
Слайд 6
Решение уравнений с использованием теоремы Виета
Приведенное квадратное уравнение
имеет вид х2 + рх + q = 0.
Его
корни удовлетворяют теореме Виета: х1 · х2 = qх1 + х2 = - р.
По коэффициентам можно предсказать знаки корней:
Свободный член «+»
Свободный член «-»
Назад
Слайд 7
Свободный член положительный.
Если свободный член приведенного уравнения положителен,
то уравнение имеет два одинаковых по знаку корня и
это зависит от второго коэффициента.Если q > 0 и р > 0 , то оба корня отрицательны.
Если q > 0 и р < 0 , то оба корня положительные.
Пример 1
х2 + 10х + 9 = 0,
х1 = - 1 и х2 = - 9,
т.к. q = 9 > 0 и р = 10 > 0;
Пример 2
х2 – 6х + 9 = 0,
х1 = 3 и х2 = 3,
т.к. q = 9 > 0 и р = - 6 < 0.
Назад
Слайд 8
Свободный член отрицательный.
Если свободный член приведенного уравнения отрицателен,
то уравнение имеет два различных по знаку корня.
Если q
< 0 и р > 0 , то больший по модулю корень будет отрицателен.Если q < 0 и р < 0, то больший по модулю корень будет положителен.
Пример 1
х2 + 2х – 8 = 0,
х1 = - 4 и х2 = 2,
т.к. q = - 8 < 0 и р = 2 > 0 ;
Пример 2
х2 – 2х – 15 = 0,
х1 = 5 и х2 = - 3,
т.к. q = - 15 < 0 и р = - 2 < 0.
Назад
Слайд 9
Решение уравнения способом «переброски».
Умножая обе части квадратного уравнения
на а, получаем уравнение
а 2 х2 + аb
х + а с = 0.Пусть а х = у, откуда ; тогда получим уравнение у2 + bу + а с = 0,
равносильное данному. С помощью теоремы Виета найдем корни: у1 и у2,
где у1 у2 = ас и у1 + у2 = - b.
Окончательно получаем и .
При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски».
Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Пример
2х2 – 11х + 15 = 0, «перебросим» коэффициент 2 к свободному члену:
у2 – 11у + 30 = 0, согласно теореме Виета найдем корни:
у1у2 = 30 и у1 + у2 = 11,
у1 = 5 и у2 = 6, окончательно получим:
х1 = 5/2 и х2 = 6/2,
х1 = 2,5 и х2 = 3.
Ответ: 2,5 и 3.
Назад
Слайд 10
Свойства коэффициентов квадратного уравнения.
Пусть дано квадратное уравнение
ах2 + bх + с = 0, где а
≠ 0.Первое свойство
Второе свойство
Третье свойство
Назад
Слайд 11
Первое свойство коэффициентов.
Если сумма коэффициентов равна нулю, т.е.
а + b + с = 0, то х1
= 1, х2 = .Доказательство: Разделим обе части уравнения на а, получим приведенное квадратное уравнение
Согласно теореме Виета: х1 · х2 = , х1 + х2 = - .
По условию, а + в + с = 0, тогда в = - а - с. Значит,
х1 · х2 = = 1 · , х1 + х2 = - = - = 1 + .
Получаем х1 = 1, х2 = , что и требовалось доказать.
Пример
3х2 + 5х – 8 = 0,
т.к. а + b + с = 0
( 3 + 5 – 8 = 0 ), то получим
х1 = 1, х2 = = -
Ответ: 1 и -
Назад
Слайд 12
Второе свойство коэффициентов.
Если а - b + с
= 0, или b = а + с,
то х1 = -1, х2 = - .Доказательство аналогично.
Пример
11х2 + 27х + 16 = 0,
Т.к. а - в + с = 0 (11 – 27 + 16 = 0 ), значит
х1 = - 1, х2 = - = - .
Ответ: -1 и -
Назад
Слайд 13
Третье свойство коэффициентов.
Если второй коэффициент b = 2k
четное число, то формулу корней можно записать в виде
.Пример
4х2 – 36х + 77 = 0,
а = 4, b = - 36, с = 77, k = - 18;
D = k2 – ас = ( - 18 )2 – 4 · 77 = 324 – 308 = 16, D > 0, два различных корня;
х1 = 5, 5 , х2 = 3,5.
Ответ: 5,5 и 3,5.
Назад
Слайд 14
Графическое решение квадратных уравнений.
Преобразуем уравнение х2 +
рх + q = 0 и получим вид:
х2 = - рх - q .Построим графики зависимостей у = х2 и у = - рх - q .
График первой зависимости - парабола, проходящая через начало координат.
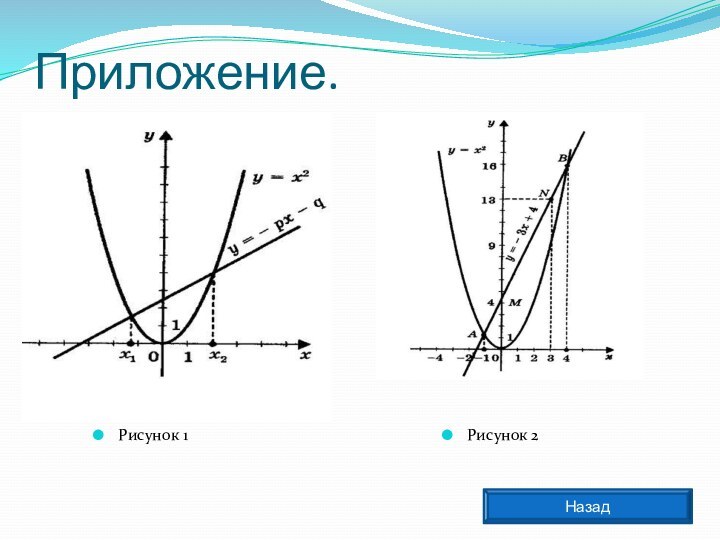
График второй зависимости – прямая . (приложение 1, рис.1).
Возможны следующие случаи:
прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
прямая и парабола могут касаться и имеют одну общую точку, значит уравнение имеет одно решение;
прямая и парабола не имеют общих точек, т. е. квадратное уравнение не имеет корней.
Назад
Примеры
Слайд 15
Примеры.
Пример 1
х2 – 3х – 4 = 0,
запишем уравнение в виде х2 = 3х +
4, рассмотрим графики зависимостей у = х2 и у = 3х + 4,Построим параболу у = х2 по координатам:
Прямую у = 3х + 4 построим по двум точкам М (0; 4) и N(3; 13) (приложение 1, рис.2).
Прямая и парабола пересекаются в двух точках А и В с абсциссами х1= -1 и х2=4.
Ответ: - 1 и 4 .
Пример 2.
х2 – 2х + 1 = 0,
Построим параболу у = х2 по координатам (см. таблицу выше) и прямую
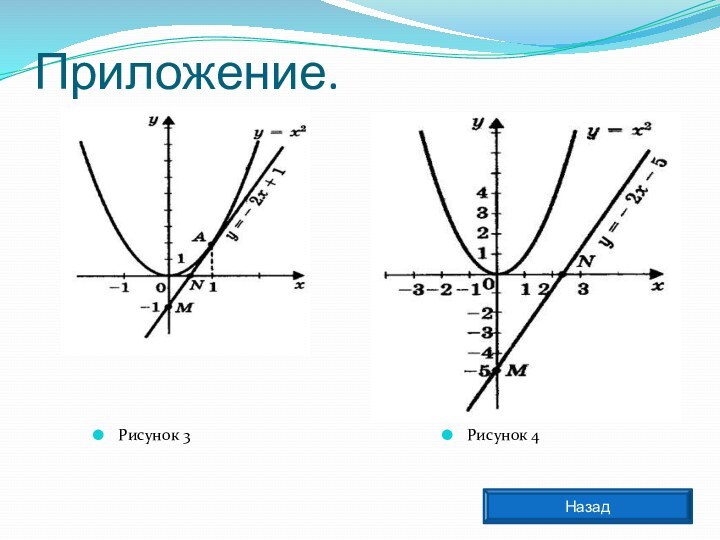
у = 2х - 1 по двум точкам М(0; -1) и N(1\2; 0) (приложение 1, рис.3).
Прямая и парабола пересекаются в точке А с абсциссой х = 1.
Ответ: 1.
Пример 3.
х2 – 2х + 5 = 0,
Построим параболу у = х2 по координатам (см. таблицу выше) и прямую
у = 2х - 5 по двум точкам М( 0; -5) и N( 2,5; 0) (приложение 1, рис.4).
Прямая и парабола не имеют точек пересечения, значит данное уравнение не имеет корней.
Ответ: нет корней.
Назад





























