Слайд 2
Анализ содержания материала
Кто не знает в какую
гавань он плывет, для того нет попутного ветра.
Сенека.
Главной целью
данной темы является: научить строить графики функций разных видов, используя характерные особенности функции, формировать навыки построения графиков функций, содержащих модуль; обратить внимание на геометрический смысл модуля.
В параграфах 28, 29, 30, 31 (Мордкович А. Г. и др. Алгебра. 7 класс: Задачник для общеобразовательных учреждений) рассматривается линейная функция
Слайд 3
Анализ содержания материала
При построении первых графиков функции
по точкам коммуникативные УУД обеспечивают социальную компетентность и учёт
позиции других учащихся, партнёров по общению или деятельности;
умение слушать и вступать в диалог;
участвовать в коллективном обсуждении проблем;
интегрироваться в группу сверстников и строить продуктивное взаимодействие и сотрудничество со сверстниками и взрослыми.
Слайд 4
Анализ содержания материала
Регулятивные универсальные учебные действия
обеспечивают организацию учащимися своей учебной деятельности. К ним относятся:
•
планирование – определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий (построение графиков функций и определение некоторых свойств ) ;
• прогнозирование – предвосхищение результата и уровня усвоения, его временных характеристик (взаимное расположение графиков функций);
• контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона;
• коррекция – внесение необходимых дополнений и корректив в план и способ действия в случае расхождения эталона, реального действия и его продукта;
Слайд 5
Анализ содержания материала
Познавательные УУД:
- осознание, что такое
свойства функции – общие, различные, существенные, несущественные, необходимые, достаточные;
-
моделирование;
- использование знаково-символической записи математического понятия;
- овладение приёмами анализа и синтеза объекта и его свойств;
- использование индуктивного умозаключения;
- выведение следствий из определения понятия;
- умение приводить контрпримеры
Слайд 6
Анализ содержания материала
Личностные УДД:
- формирование ценностных ориентаций
(саморегуляция, стимулирование, достижение и др.);
- формирование математической компетентности.
Таким образом,
материал параграфа учебника удовлетворяет требованиям современных стандартов образования, позволяет прививать учащимся навыки УУД.
Слайд 7
Подбор дополнительных заданий
№1
Найдите площадь треугольника, ограниченного осями координат
и прямой
y = ‒ 2x+2.
Познавательные УУД:
- моделирование;
-
использование знаково-символической записи математического понятия;
- овладение приёмами анализа и синтеза объекта и его свойств;
- использование индуктивного умозаключения;
Личностные УДД:
- формирование математической компетентности.
Логические УДД:
- анализ объектов с целью выделения признаков (существенных, несущественных);
- синтез — составление целого из частей, в том числе самостоятельное достраивание с восполнением недостающих компонентов
Слайд 8
Подбор дополнительных заданий
№2
На координатной плоскости лежат 4 точки
A(1;5), B(-1;1), C(1,5;6), D(7;12).
Лежат ли они на одной
прямой?
Познавательные УУД:
- осознание, что такое свойства функции
- моделирование;
- использование знаково-символической записи математического понятия;
- использование индуктивного умозаключения;
- выведение следствий из определения понятия;
Личностные УДД:
- формирование математической компетентности.
Регулятивные УУД:
- умение выделять свойства в изучаемых объектах и дифференцировать их;
Слайд 9
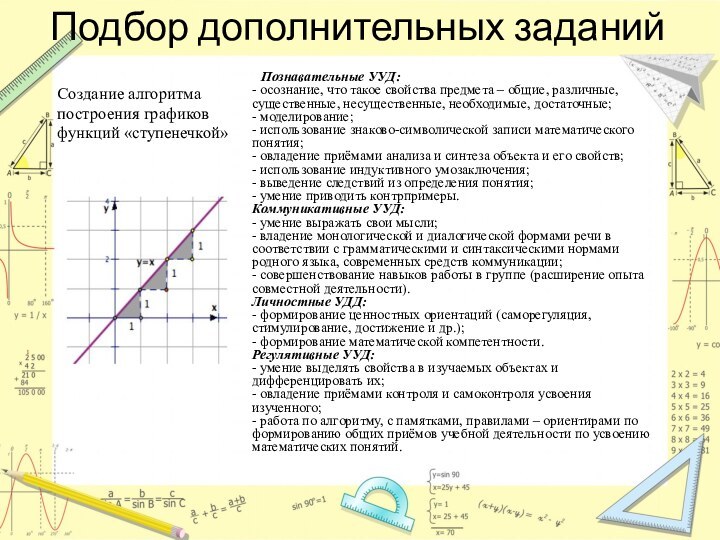
Подбор дополнительных заданий
Создание алгоритма
построения графиков
функций «ступенечкой»
Познавательные
УУД:
- осознание, что такое свойства предмета – общие, различные,
существенные, несущественные, необходимые, достаточные;
- моделирование;
- использование знаково-символической записи математического понятия;
- овладение приёмами анализа и синтеза объекта и его свойств;
- использование индуктивного умозаключения;
- выведение следствий из определения понятия;
- умение приводить контрпримеры.
Коммуникативные УУД:
- умение выражать свои мысли;
- владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка, современных средств коммуникации;
- совершенствование навыков работы в группе (расширение опыта совместной деятельности).
Личностные УДД:
- формирование ценностных ориентаций (саморегуляция, стимулирование, достижение и др.);
- формирование математической компетентности.
Регулятивные УУД:
- умение выделять свойства в изучаемых объектах и дифференцировать их;
- овладение приёмами контроля и самоконтроля усвоения изученного;
- работа по алгоритму, с памятками, правилами – ориентирами по формированию общих приёмов учебной деятельности по усвоению математических понятий.
Слайд 10
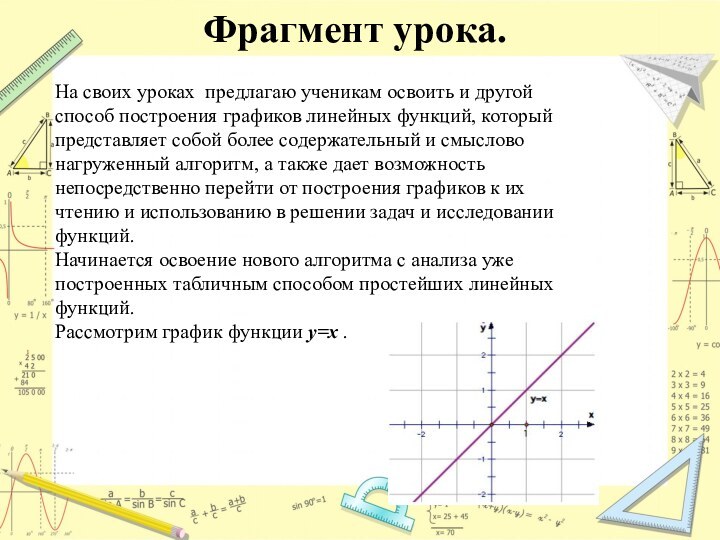
Фрагмент урока.
На своих уроках предлагаю ученикам освоить и
другой способ построения графиков линейных функций, который представляет собой
более содержательный и смыслово нагруженный алгоритм, а также дает возможность непосредственно перейти от построения графиков к их чтению и использованию в решении задач и исследовании функций.
Начинается освоение нового алгоритма с анализа уже построенных табличным способом простейших линейных функций.
Рассмотрим график функции y=x .
Слайд 11
Фрагмент урока.
Будем двигаться по точкам этого графика, начиная
с точки (0,0) начала координат, через которую он проходит.
Видим, что при сдвиге на одну единицу вправо по оси Х, значение функции у=х вырастает также на единицу. За каждый шаг вправо на единицу (то есть в направлении оси абсцисс) график поднимается вверх на единицу.
Таким образом, получается характерная “лесенка” ступенек, формирующих график
функции: вправо на 1
–вверх на 1 и т.д.
Слайд 12
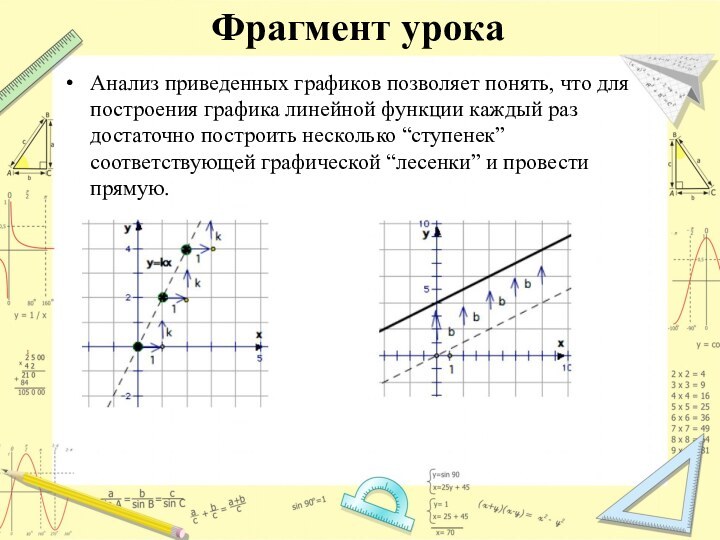
Фрагмент урока
Анализ приведенных графиков позволяет понять, что для
построения графика линейной функции каждый раз достаточно построить несколько
“ступенек” соответствующей графической “лесенки” и провести прямую.
Слайд 13
Фрагмент урока
Общая характеристика графической “лесенки” и ее особенностей:
“Лесенка” всегда идет вправо (в сторону роста х);
Если в
формуле, задающей функцию y=kx+b коэффициент k>0, то “лесенка” идет вверх;
Если k<0, то “лесенка” идет вниз;
Высота каждой ступеньки одинакова и определяется числовым значением коэффициента k (чем k больше, тем выше ступенька);
За каждую единицу по х функция вырастает по у на k, то
Есть k – это скорость роста функции;
Скорость роста линейной функции не меняется, ступеньки нашей “лесенки” всегда одной высоты, именно поэтому функция и представляет собой прямую.
Слайд 14
Фрагмент урока
Опыт показывает, что изложенный способ построения и
чтения графиков линейных функций легко и достаточно быстро усваивается.
Учащиеся начинают отличать по графику возрастающие и убывающие функции, определять графики с большей, меньшей или одинаковой скоростью роста функции.
Эти навыки, помимо владения названной темой,
готовят учащихся к восприятию
понятия производной, к
исследованию и анализу более
сложных функциональных
зависимостей.