уравнение сферы в заданной прямоугольной системе координат
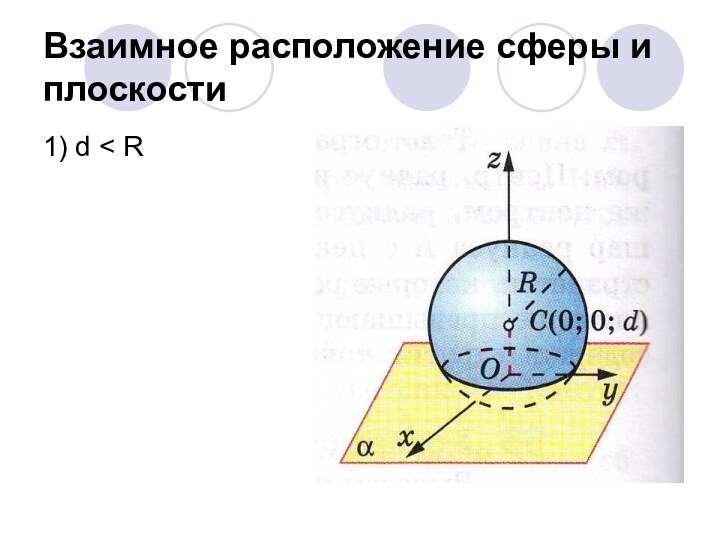
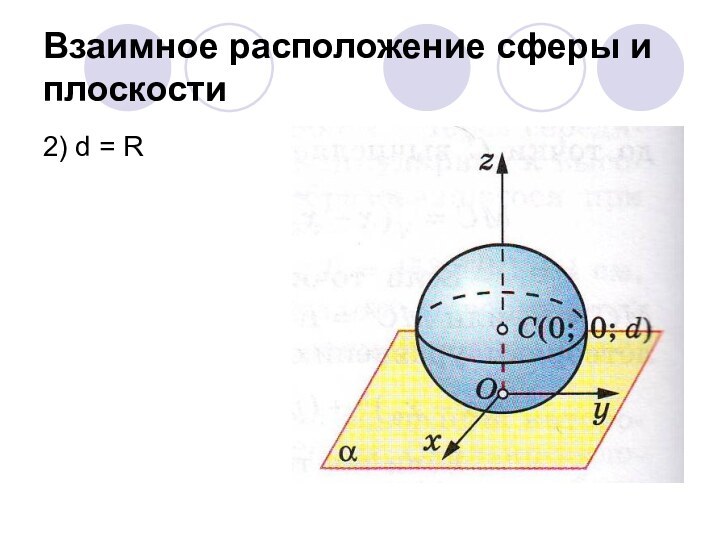
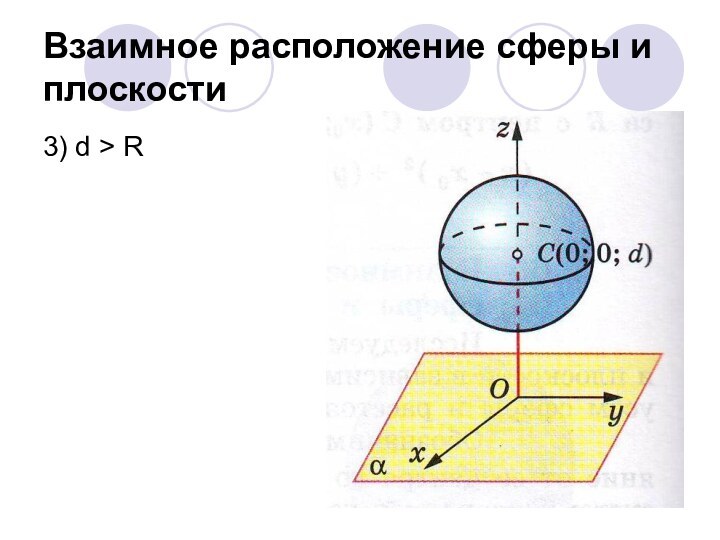
Рассмотреть возможные случаи
взаимного расположения сферы и плоскостиФормировать навык решения задач по теме
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


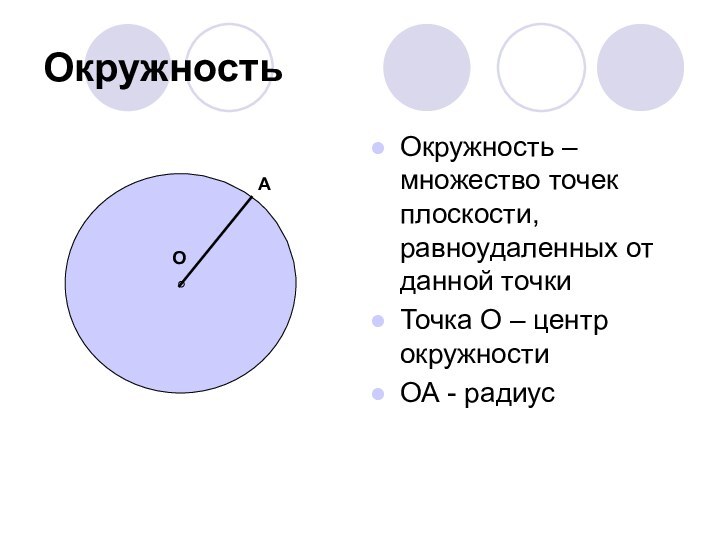
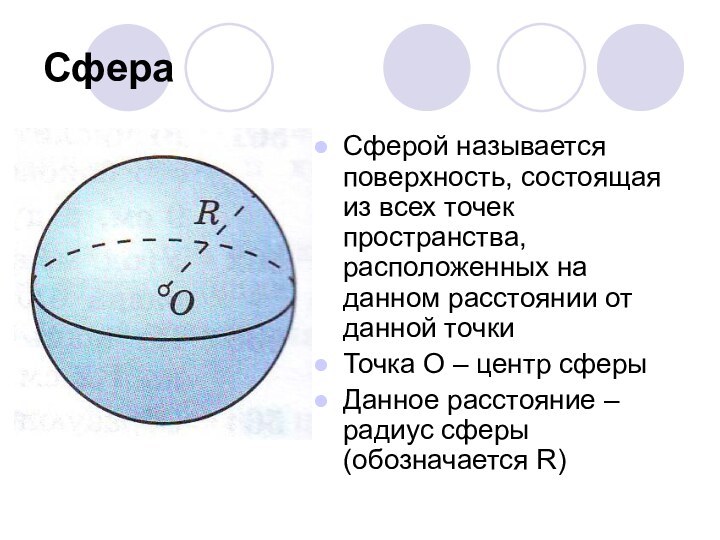

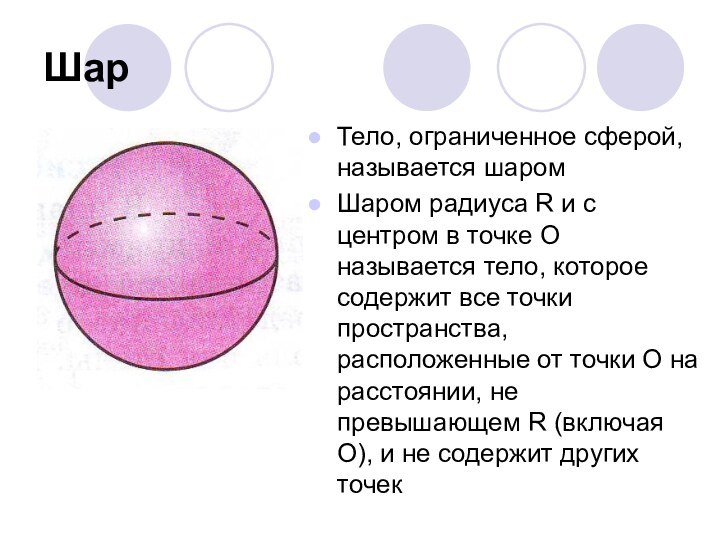





О