- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Аксиомы стереометрии
Содержание
- 2. ГеометрияПланиметрияСтереометрия stereos телесный, твердый, объемный, пространственный
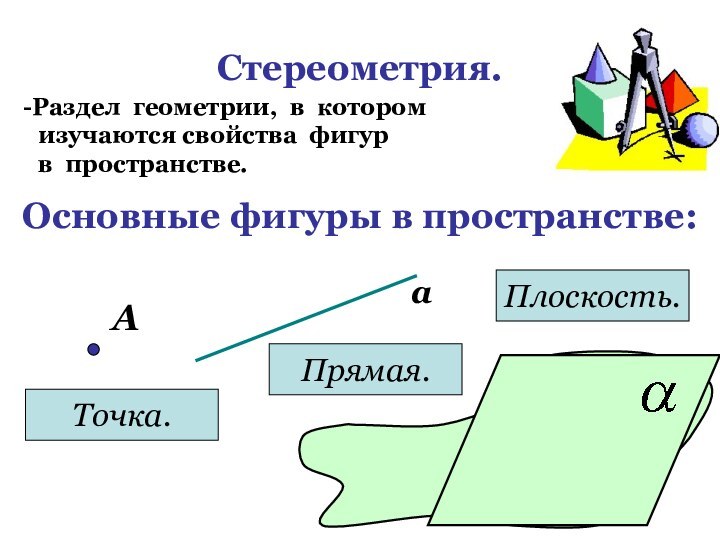
- 3. Стереометрия.Раздел геометрии, в котором изучаются свойства фигур в пространстве.Основные фигуры в пространстве:АТочка.аПрямая.Плоскость.
- 4. A, B, C, …a, b, c, …илиAВ, BС, CD, …
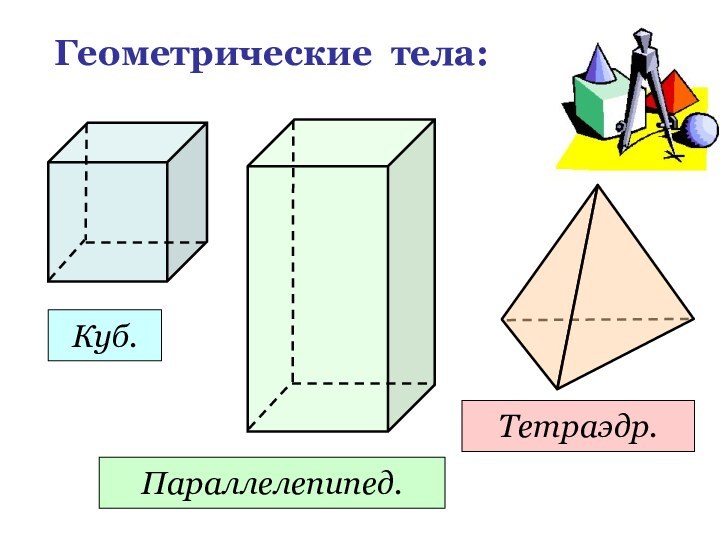
- 5. Геометрические тела:Куб.Параллелепипед.Тетраэдр.
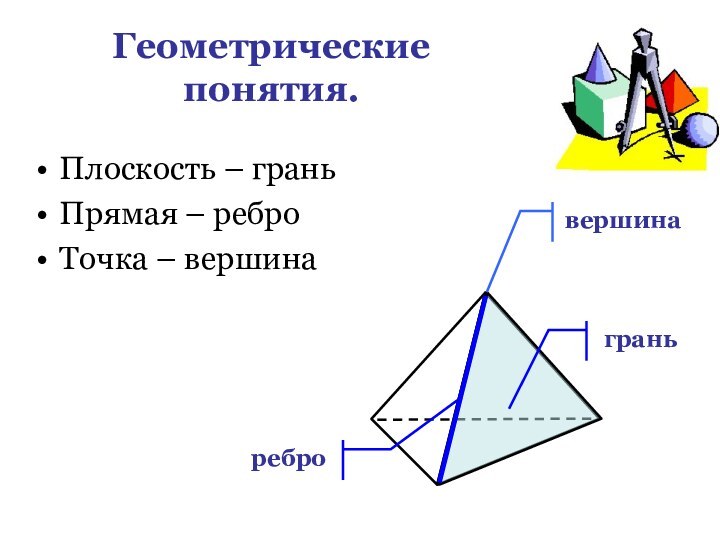
- 6. Геометрические понятия.Плоскость – граньПрямая – реброТочка – вершинавершинаграньребро
- 7. Аксиома(от греч. axíõma – принятие положения)исходное положение научной теории, принимаемое без доказательства
- 8. АКСИОМЫпланиметриястереометрия1. Каждой прямой принадлежат по крайней мере
- 9. А3. Если две плоскости имеют общую точку,
- 10. Аксиомы стереометрии описывают:А1.А2. А3. АВСbСпособ задания плоскости.bАВВзаимное расположение прямой и плоскостиabВзаимное расположение плоскостей
- 11. Способы задания плоскости1. Плоскость можно провести через
- 12. Взаимное расположение прямой и плоскости.Прямая лежит в
- 13. Следствия из аксиом стереометрии.Через прямую и не
- 14. Прочти чертежAС
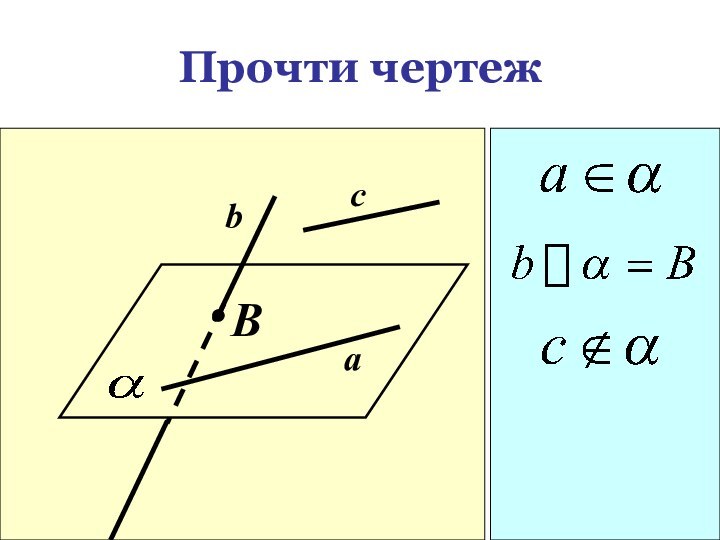
- 15. Прочти чертежBcba
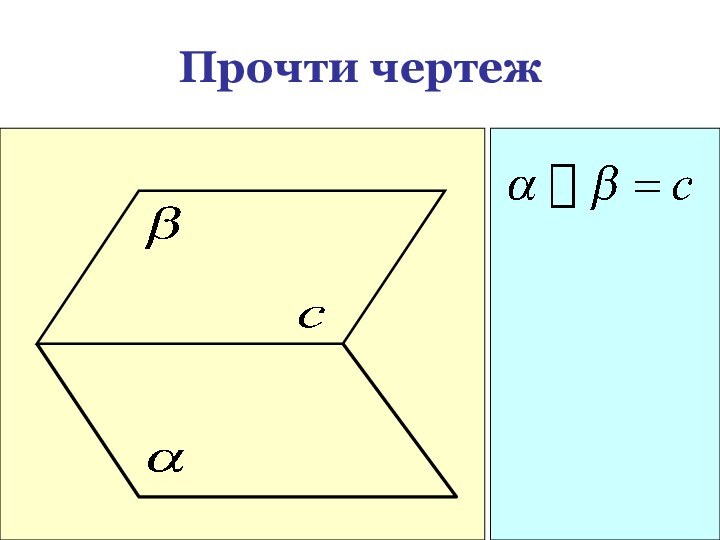
- 16. Прочти чертеж
- 17. Пользуясь данным рисунком, назовите:а) четыре точки, лежащие
- 18. Пользуясь данным рисунком, назовите:а) две плоскости, содержащие
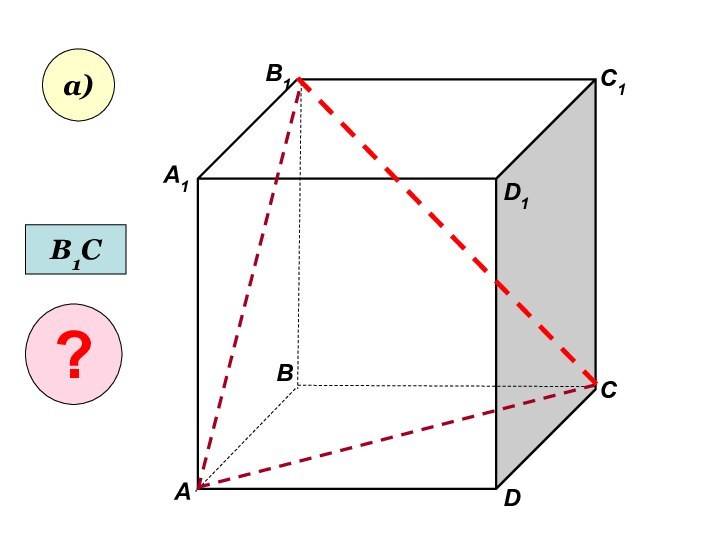
- 19. Пользуясь данным рисунком, назовите:а) три плоскости, содержащие прямую В1С; прямую АВ1;
- 20. АА1ВВ1СD1DC1а)В1С?
- 21. АА1ВВ1СD1DC1а)В1С?
- 22. Пользуясь данным рисунком, назовите:а) три плоскости, содержащие
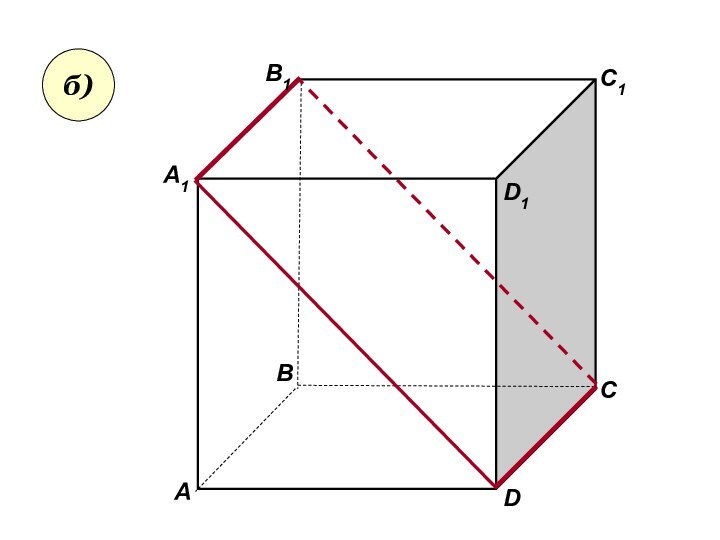
- 23. АА1ВВ1СD1DC1б)
- 24. Пользуясь данным рисунком, назовите:а) три плоскости, содержащие
- 25. АА1ВВ1СD1DC1в)
- 26. Пользуясь данным рисунком, назовите:а) три плоскости, содержащие
- 27. Закрепление изученного материала. № 1; № 2 (б,д);
- 28. Домашнее задание:Выучить аксиомыи следствия из них.Задания 4
- 29. Скачать презентацию
- 30. Похожие презентации






Слайд 7
Аксиома
(от греч. axíõma – принятие положения)
исходное положение научной
теории, принимаемое без доказательства
Слайд 8
АКСИОМЫ
планиметрия
стереометрия
1. Каждой прямой принадлежат по крайней мере две
точки
2. Имеются по крайней мере три точки, не
лежащие на одной прямой3. Через любые две точки проходит прямая, и притом только одна.
Характеризуют взаимное расположение точек и прямых
Основное понятие геометрии «лежать между»
4. Из трех точек прямой одна и только одна лежит между двумя другими.
А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
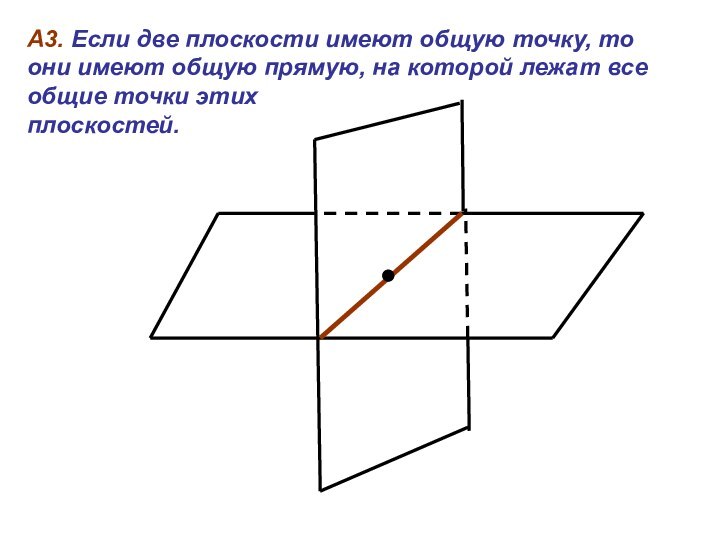
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Слайд 9 А3. Если две плоскости имеют общую точку, то
они имеют общую прямую, на которой лежат все общие
точки этих плоскостей.
Слайд 10
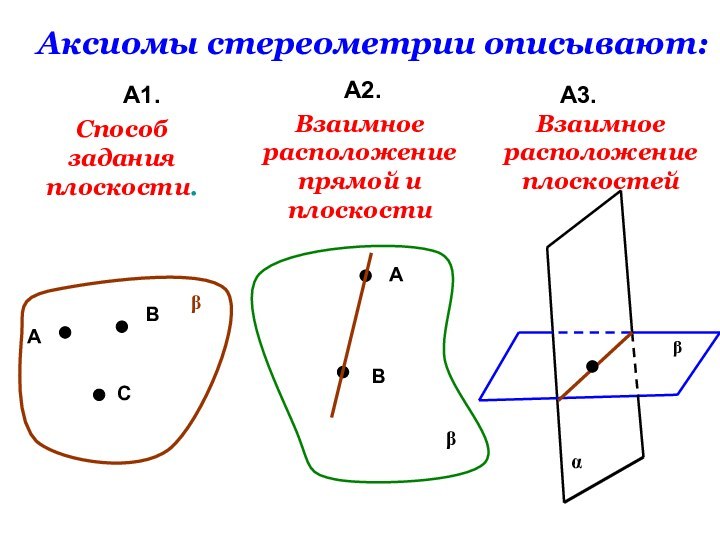
Аксиомы стереометрии описывают:
А1.
А2.
А3.
А
В
С
b
Способ задания плоскости.
b
А
В
Взаимное расположение
прямой и плоскости
a
b
Взаимное расположение плоскостей
Слайд 11
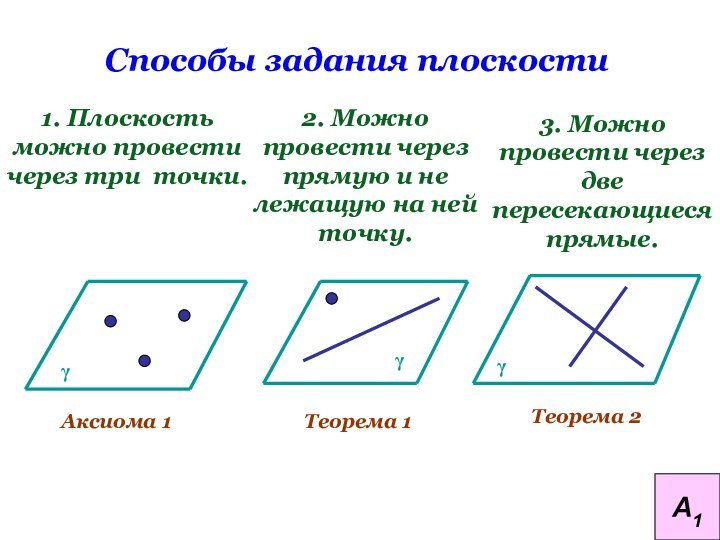
Способы задания плоскости
1. Плоскость можно провести через три
точки.
2. Можно провести через прямую и не лежащую на
ней точку.Аксиома 1
Теорема 1
Теорема 2
3. Можно провести через две пересекающиеся прямые.
А1
Слайд 12
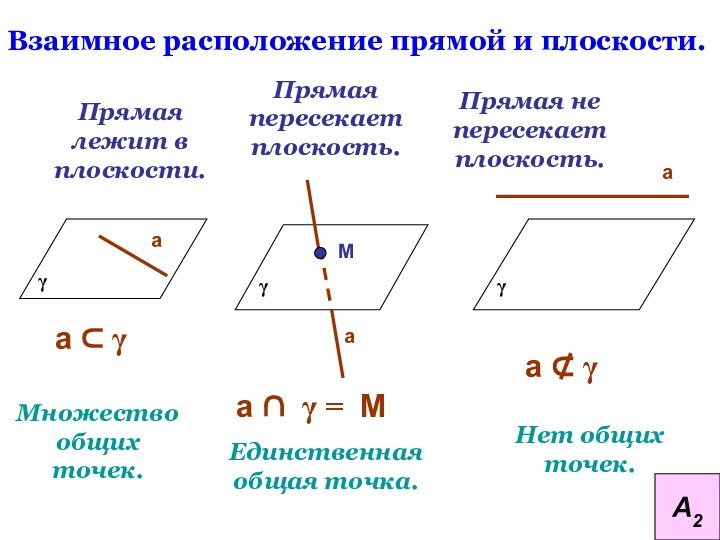
Взаимное расположение прямой и плоскости.
Прямая лежит в плоскости.
Прямая
пересекает плоскость.
Прямая не пересекает плоскость.
Множество общих точек.
Единственная общая точка.
Нет
общих точек.g
а
g
а
М
g
а
а Ì g
а Ç g = М
а Ë g
А2
Слайд 13
Следствия из аксиом стереометрии.
Через прямую и не лежащую
на ней точку проходит плоскость, и притом только одна.
Через
две пересекающиеся прямые проходит плоскость, и притом только одна.
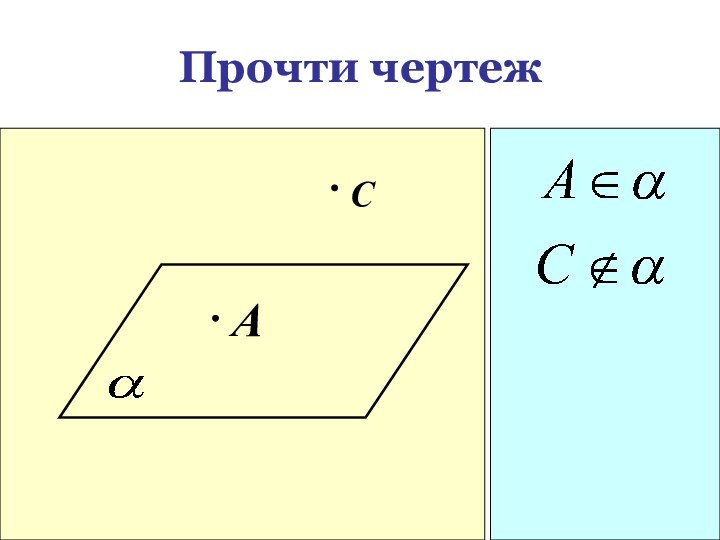
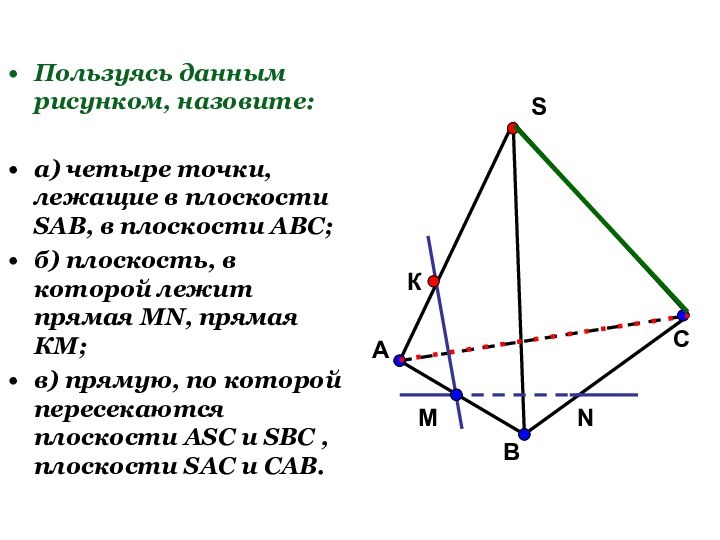
Слайд 17
Пользуясь данным рисунком, назовите:
а) четыре точки, лежащие в
плоскости SAB, в плоскости АВС;
б) плоскость, в которой лежит
прямая MN, прямая КМ;в) прямую, по которой пересекаются плоскости ASC и SBC , плоскости SAC и CAB.
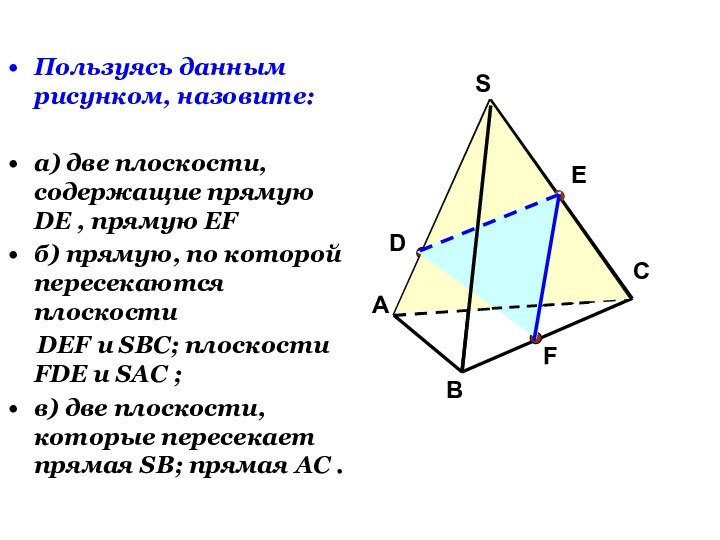
Слайд 18
Пользуясь данным рисунком, назовите:
а) две плоскости, содержащие прямую
DE , прямую EF
б) прямую, по которой пересекаются плоскости
DEF и SBC; плоскости FDE и SAC ;в) две плоскости, которые пересекает прямая SB; прямая AC .
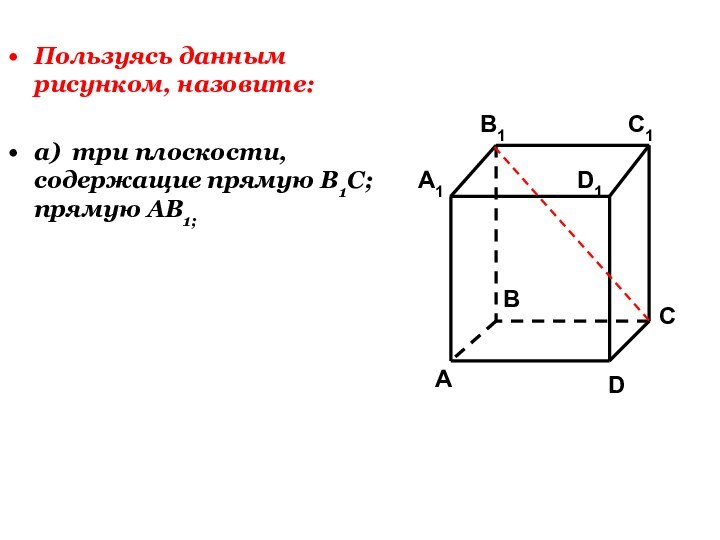
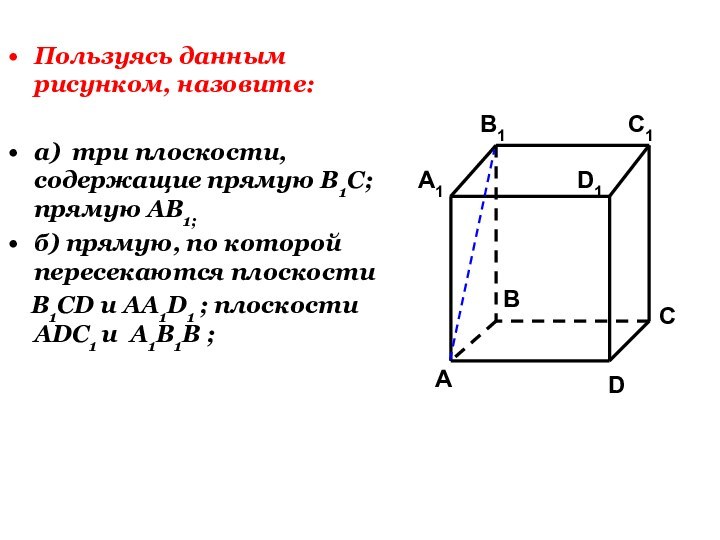
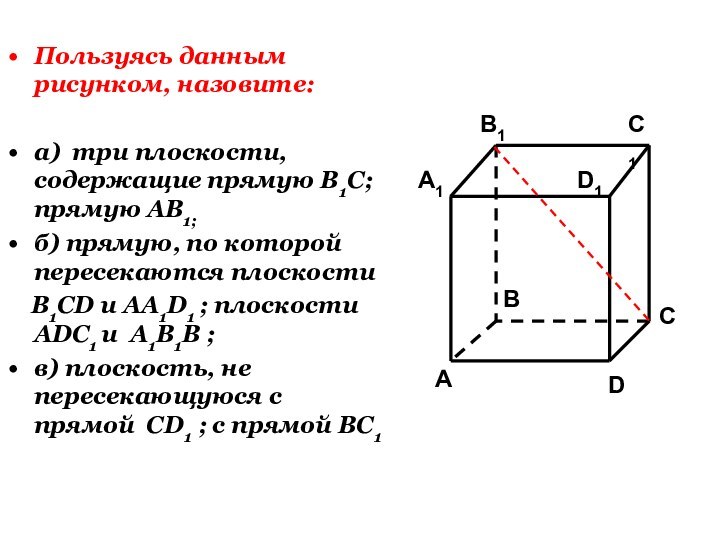
Слайд 22
Пользуясь данным рисунком, назовите:
а) три плоскости, содержащие прямую
В1С; прямую АВ1;
б) прямую, по которой пересекаются плоскости
B1CD и AA1D1 ; плоскости ADC1 и A1B1B ;C1
C
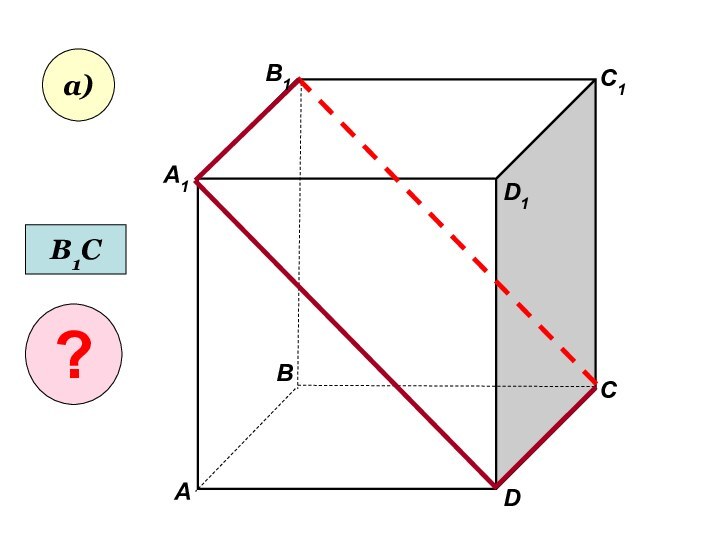
Слайд 24
Пользуясь данным рисунком, назовите:
а) три плоскости, содержащие прямую
В1С; прямую АВ1;
б) прямую, по которой пересекаются плоскости
B1CD и AA1D1 ; плоскости ADC1 и A1B1B ;в) плоскость, не пересекающуюся с прямой CD1 ; с прямой BC1
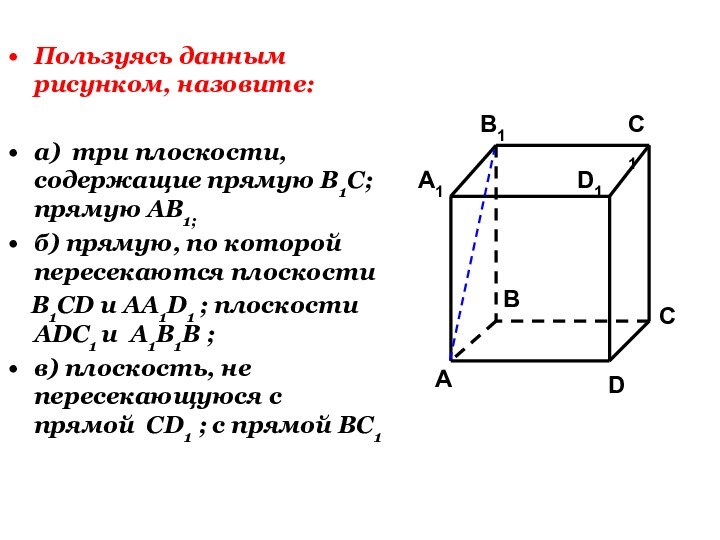
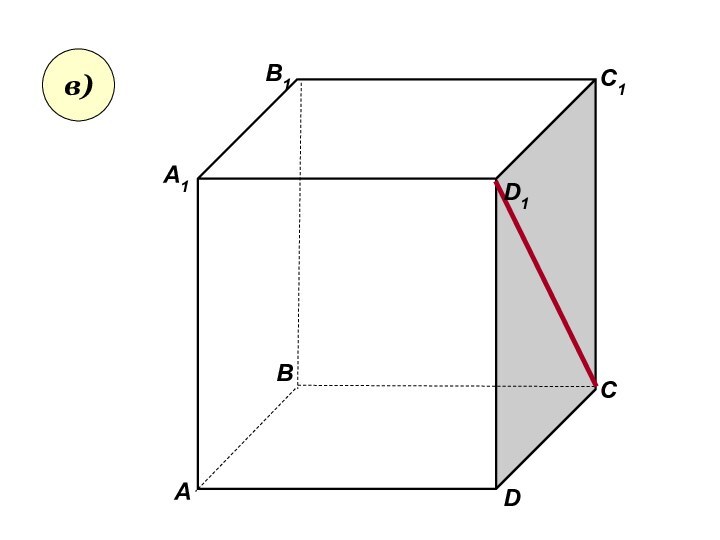
Слайд 26
Пользуясь данным рисунком, назовите:
а) три плоскости, содержащие прямую
В1С; прямую АВ1;
б) прямую, по которой пересекаются плоскости
B1CD и AA1D1 ; плоскости ADC1 и A1B1B ;в) плоскость, не пересекающуюся с прямой CD1 ; с прямой BC1
Слайд 28
Домашнее
задание:
Выучить аксиомы
и следствия из них.
Задания 4 – 12
в
рабочей тетради.
2) П. 1-3
стр. 4 – 7.
3) №№
4; 6; 10.Успехов!