Презентация на тему Симметрия 6 класс

симметрией.

Задачи:
1. Дать представление о симметрии в окружающем мире, сформировать понятие симметрии, познакомить основными ее видами, приобрести опыт построения симметричных фигур.
2.Развитие математического мышления и логической речи учащихся, воображения, умения делать выводы, высказывать свои чувства и мысли; расширять кругозор учащихся, умение видеть знакомое в незнакомом.
3. Развитие познавательной активности, интереса к предмету, творческой активности.

Виды симметрии
5. Вопросы
6. Дополнительные задания
7. Практическая работа №1
8.

Практическая работа №2
9. Заключение (урок последний, но не прощальный)

Математика  …выявляет порядок,
симметрию, и определенность, а это –
важнейшие виды прекрасного.
                                                          Аристотель

«Симметрия» - слово греческого происхождения. Оно означает соразмерность, наличие определенного порядка, закономерности в расположении частей.
Люди с давних времен использовали симметрию в рисунках, орнаментах, предметах быта.
Симметрия широко распространена в природе. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, мозаике в храме, морской звезде.
Симметрия широко используется на практике, в строительстве и технике. Это строгая симметрия в форме античных зданий, гармоничные древнегреческие вазы, здании Кремля, машинах, самолетах и многом другом.
Использование симметрии в бордюрах и паркетах.

Введение.

частей чего-нибудь по противоположным сторонам от точки, прямой или

плоскости.
Толковый словарь русского языка
С.И. Ожегова и Н.Ю. Шведовой.
«Симметрия» (нем. Symmetrie, франц. symetrie, греч. symmetria ) – соразмерность, пропорциональность в расположении частей чего-нибудь по обе стороны от середины, центра.
Толковый словарь
иностранных слов Л.П. Крысина.
«Симметрия» - соразмерность, в широком смысле – инвариантность (неизменность) структуры, свойств, формы материального объекта относительно его преобразований ( т.е. изменений ряда физических свойств). Симметрия лежит в основе законов сохранения.
Большая энциклопедия
Кирилла и Мефодия.

точки, лежащие на одном перпендикуляре к данной плоскости (или

прямой) по разные стороны и на одинаковом расстоянии от неё, называются симметричными относительно этой плоскости (или прямой).
Фигура (плоская или пространственная) симметрична относительно прямой (оси симметрии) или плоскости (плоскости симметрии), если её точки попарно обладают указанным свойством.
Фигура симметрична относительно точки (центр симметрии), если её точки попарно лежат на прямых, проходящих через центр симметрии, по разные стороны и на равных расстояниях от неё.
Большая энциклопедия
Кирилла и Мефодия.

однако в 38 предложении 11 книги содержится понятие пространственной

оси симметрии. Впервые понятие центра симметрии встречается в 16 веке в одной из теорем Клавиуса, гласящей: если параллелепипед рассекается плоскостью, проходящей через центр, то он разбивается пополам и, наоборот, если параллелепипед рассекается пополам , то плоскость проходит через центр. Лежандр, который впервые ввел в элементарную геометрию элементы учения о симметрии, говорит только о симметрии относительно плоскости и дает следующее определение: две точки А и В симметричны относительно плоскости а, если последняя перпендикулярна к АВ в середине этого отрезка. Лежандр показывает, что у прямого параллелепипеда имеются 3 плоскости симметрии, перпендикулярные к ребрам, а у куба 9 плоскостей симметрии, из которых 3 перпендикулярны к ребрам, а другие 6 проходят через диагонали граней. В учебнике наглядной геометрии 20 века (например , Бореля) учение о симметрии впервые излагается более полно и систематически и кладется даже в основу геометрических выводов.

На плоскости

На прямой



Зеркальная Осевая



Центральная Центральная


Центральная

Поворотная

Движение плоскости - это отображение плоскости на себя, сохраняющее расстояния. Итак, осевая и центральная симметрия представляют собой отображение плоскости на себя, которое сохраняет расстояния между точками.

них имеет свое название. Рассмотрим основные виды симметрии.




Центральная
Осевая
Зеркальная







Виды симметрии

относительно точки.
Опр.: Точки А и В симметричны относительно некоторой

точки О, если точка О является серединой отрезка АВ.
Опр.: Точка О называется центром симметрии фигуры, а фигура называется центрально-симметричной.
Свойство: Фигуры, симметричные относительно некоторой точки, равны.

РИС. 2

РИС. 1

С 1, симметричный треугольнику АВС, относительно центра (точки) О.

Для этого:
Соединим точки А,В,С с центром О
и продолжим эти отрезки;
2. Измерим отрезки АО, ВО, СО и отложим с другой стороны от
точки О, равные им отрезки
(АО=А 1 О 1, ВО=В 1 О 1, СО=С 1 О 1 );
3. Соединим получившиеся точки отрезками А 1 В 1, А 1 С 1,
В 1 С 1.
4. Получили ∆А 1 В 1 С 1 симметричный ∆АВС.

А

В

С

О

С

1

А

В

1

1

Построение:

симметрии:
А Б В Г Д Е Ж З И

К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я?
2. Какие две цифры переходят друг в друга при центральной симметрии?
3. На рисунке изображена часть фигуры, центром симметрии которой является точка М. Начертите эту фигуру в тетради.

М

проведенной оси (прямой).
Опр.: Точки А и В симметричны относительно

некоторой прямой а, если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии.
Опр.: Осью симметрии называется прямая при перегибании по которой «половинки» совпадут, а фигуру называют симметричной относительно некоторой оси.
Свойство: Две симметричные фигуры равны.

Рис. 1

Рис. 2

А1В1С1, симметричный треугольнику АВС относительно прямой а.
Для

этого:
1. Проведем из вершин треугольника АВС прямые, перпендикулярные прямой а и продолжим их дальше.
2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. Соединим получившиеся точки отрезками А1В1, В1С1, В1С1.
4. Получили ∆ А1В1С1 симметричный ∆АВС.

А

В

С

С

А

В

1

1

1

Построение:

1

а).одну ось симметрии; б). Две оси симметрии; в) много

осей симметрии:
А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ч Ш Щ Ъ Ы Ь Э Ю Я?
2. Прямая Ор – ось симметрии треугольника КОМ. Назовите все равные элементы треугольников КОР и РОМ. Каков вид этих треугольников?
Рисунок:




3. Постройте слово, симметричное относительно прямой а.

О

М

К

Р

а

У р о к

симметрии «разрезает» фигуру на две равные части.
На рисунках изображены

пространственные фигуры, симметричные относительно некоторой плоскости.

Рис. 1

Рис. 2

Рис. 3

Рис. 4

Рис. 5

Ответ: а). б). в)..



2. а). Прочитайте слово, отраженное в зеркале.
б). Зеркало поможет вам догадаться, какое слово не дописано.

а). б).

слово «симметрия» в узком и широком смыслах слова?
Приведите примеры

симметрии, встречающейся в нашей жизни.
Кто впервые в наглядной геометрии более подробно изложил учение о симметрии, которое кладется в основу геометрических выводов?
Что означает центральная симметрия?
Что означает осевая симметрия?
Что означает зеркальная симметрия?

себе. Где расположен центр этой симметрии?
При некоторой центральной симметрии

прямоугольник симметричен сам себе. Где расположен центр симметрии?
Треугольник KMN центрально симметричен треугольнику AKN. Где расположен центр этой симметрии?
Может ли треугольник иметь: а). одну; б) две; в). три оси симметрии?
Треугольник KMN симметричен треугольнику NAK относительно некоторой прямой. Сделай схематический рисунок (рассмотрите все случаи).

Почему?







7. Скопируйте фигуру в тетрадь и найдите ее центр

симметрии.

Дополнительные задания

(на доске и в тетрадях).
А).

Б). В).





9. Выполнить построение фигуры, симметричной относительно прямой а (на доске и в тетрадях).
А). Б). В).

А

В

О

О

О

а

К

М

а

а

а

Дополнительные задания

к, и фигуру А2, симметричную А1 относительно прямой m.

Как еще можно получить фигуру А2 из фигуры А?




11. Найдите центр симметрии фигуры, состоящей из двух окружностей.
А). Б). В).

к

m

А

Дополнительные задания

места встречи равные расстояния. Укажите место встречи кораблей.




13. Постройте

отрезок, симметричный данному относительно точки А, а затем отрезок, симметричный получившемуся относительно точки В.
а). б).

А

А

В

В

АВСДКМ. Какая точка симметрична вершине М относительно точки О?

Какая фигура симметрична относительно точки О отрезку АВ? Треугольнику КОД? Четырехугольнику АВКМ?

А

В

С

Д

К

М

О

центре окружности.

точке пересечения диагоналей.

О

АВ относительно точки О симметричен отрезок КД;
Треугольнику КОД

относительно точки О симметричен треугольник АОВ;
Четырехугольнику АВКМ относительно точки О симметричен четырехугольник КВСД;

прямую k и отметьте точки А, В и С,

не лежащие на этой прямой. Выполните следующие задания:
1. Постройте точки, симметричные точкам А, В и С относительно прямой k. Обозначьте их.
2. Запишите пары точек, симметричных относительно прямой k.
2 вариант.
Начертите отрезок АВ и проведите прямую m, его не пересекающую. Выполните следующие задания:
1. Постройте отрезок, симметричный отрезку АВ относительно прямой m. Обозначьте его.
2. Запишите пары концов отрезка, симметричных относительно прямой m.
3 вариант.
Начертите ломаную ВОС и проведите прямую k, ее не пересекающую. Выполните следующие задания:
1. Постройте ломаную, симметричную ломаной ВОС относительно прямой k. Обозначьте ее.
2. Запишите пары отрезков ломаной, симметричных относительно прямой k.
4 вариант.
Начертите треугольник АВС и проведите прямую m, его не пересекающую. Выполните следующие задания:
1. Постройте треугольник, симметричный треугольнику АВС относительно прямой m. Обозначьте его.
2. Запишите пары сторон треугольника, симметричных относительно прямой m.

1
А 1
С 1
Пары симметричных точек, относительно прямой k :

А и А1, В и В1, С и С1.

Вариант 2.

А

В

m

k

В 1

А 1

Пары концов отрезков, симметричных относительно прямой m: А и А1, В и В1.

4.
В
О
С
k



C 1
О 1
В 1
Пары отрезков ломаной, симметричных относительно прямой

k: ОВ и О1 В1, ОС и О1 С1.

А

В

С

А 1

В 1

С 1

Пары сторон треугольника, симметричных относительно прямой m: АВ И А1 В1, ВС и В1 С1, АС и А1 С1.

симметрии»
1 вариант.
Скопируйте рисунок в тетрадь и выполните следующие задания:

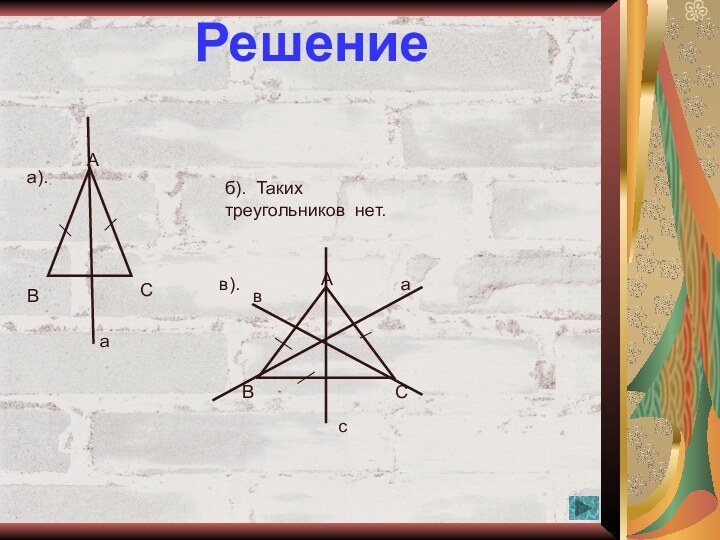
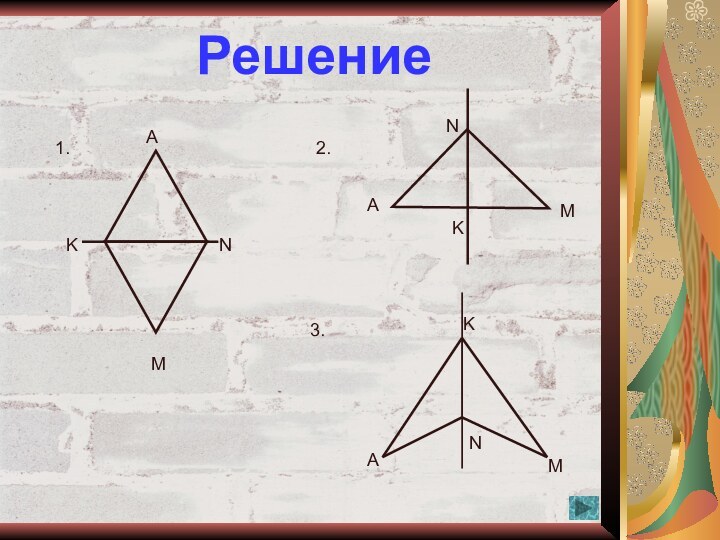
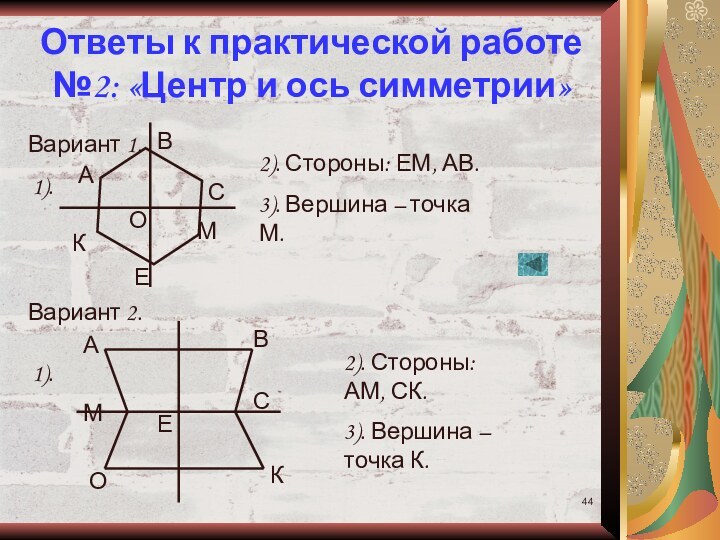
1. Проведите оси симметрии шестиугольника АВСМЕК.
2. Укажите сторону шестиугольника, симметричную стороне ВС относительно
каждой его оси симметрии.
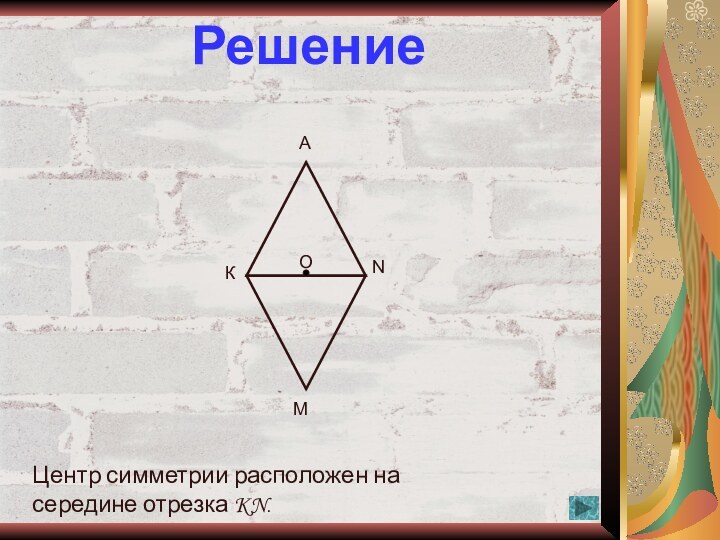
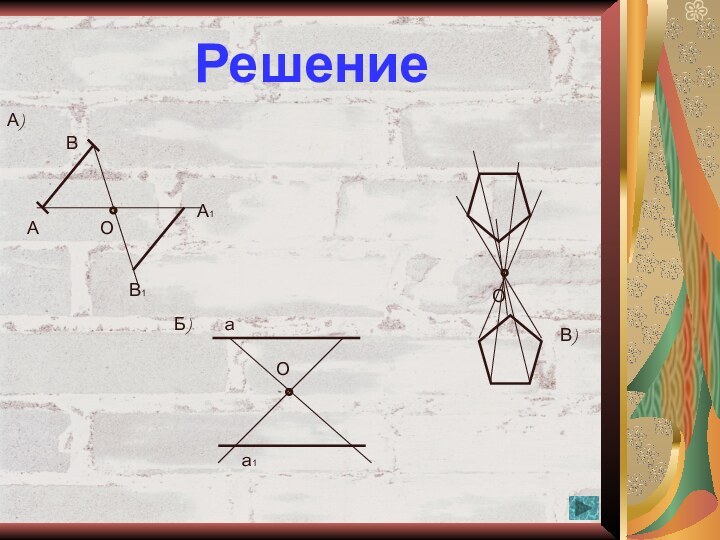
3. Найдите центр симметрии фигуры и обозначьте его буквой О. Укажите
вершину шестиугольника, симметричную вершине А относительно центра.
2 вариант.
Скопируйте рисунок в тетрадь и выполните следующие задания:
1. Проведите оси симметрии шестиугольника АВСКОМ.
2. Укажите сторону шестиугольника, симметричную стороне ВС относительно
каждой его оси симметрии.
3. Найдите центр симметрии фигуры и обозначьте его буквой Е. Укажите
вершину шестиугольника, симметричную вершине А относительно центра.
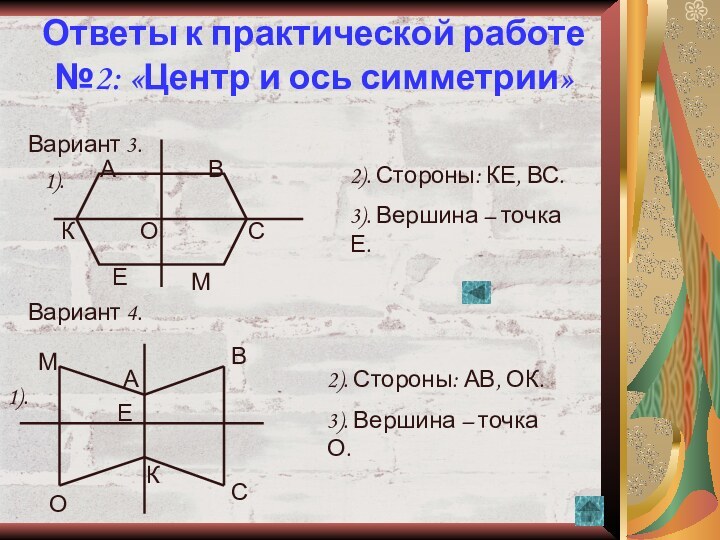
3 вариант.
Скопируйте рисунок в тетрадь и выполните следующие задания:
1. Проведите оси симметрии шестиугольника АВСМЕК.
2. Укажите сторону шестиугольника, симметричную стороне АК относительно
каждой его оси симметрии.
3. Найдите центр симметрии фигуры и обозначьте его буквой О. Укажите
вершину шестиугольника, симметричную вершине В относительно центра.
4 вариант.
Скопируйте рисунок в тетрадь и выполните следующие задания:
1. Проведите оси симметрии шестиугольника АВСКОМ.
2. Укажите сторону шестиугольника, симметричную стороне МА относительно
каждой его оси симметрии.
3.Найдите центр симметрии фигуры и обозначьте его буквой Е. Укажите
вершину шестиугольника, симметричную вершине В относительно центра.

А

В

С

М

Е

К

А

В

С

М

Е

К

А

В

С

К

О

М

М

А

В

О

К

С

симметрии»
Вариант 1.




Вариант 2.


А
В
С
М
Е
К
1).
2). Стороны: ЕМ, АВ.
3). Вершина – точка

М.

О

А

В

С

К

О

М

1).

2). Стороны: АМ, СК.
3). Вершина – точка К.

Е

симметрии»
Вариант 3.




Вариант 4.



А
В
С
М
Е
К
1).
2). Стороны: КЕ, ВС.
3). Вершина – точка

Е.

О

А

В

С

К

О

М

1).

2). Стороны: АВ, ОК.
3). Вершина – точка О.

Е

частям и осям симметрии.
а).

б) в)





2. Проведите все оси симметрии фигуры.
а). б).

ее.







4. Точка М – центр симметрии фигуры, часть которой

изображена на рисунке. Постройте ее.

М

слова.
Тема, которую мы изучаем.
Ученый, который впервые ввел в

элементарную геометрию элементы учения о симметрии.
Симметрия относительно прямой.
Прямая, при перегибании по которой «половинки» совпадут.
Точка, относительно которой фигуры симметричны.
Основное свойство симметрии, при котором фигуры …
Симметрия относительно точки.
Симметрия относительно плоскости.
Еще один вид симметрии, о котором мало упоминают в школе.