- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Статистика в клеточной биологии и в клинических исследованиях
Содержание
- 2. Упорядоченный посев и пуассонер – высокоточная техника количественной микробиологииМЕДИЦИНА. XXI ВЕК№ 2 (11) 2008, c. 92-97
- 3. Распределение ПуассонаРаспределение числа событий, происходящих в фиксированном
- 4. Распределение ПуассонаP(k) = e-λλk/k!e = 2,71828 –
- 5. Пуассонер, упорядоченный посевН. Н. Хромов-Борисов, Jenifer Saffi
- 6. Сравнение упорядоченного посева с обычным методом
- 7. Воспроизводимость
- 8. Распределения числа колоний дрожжей на десяти чашках
- 9. Пуассоновость
- 10. Среднеквадратичное отклонение (стандартная ошибка среднего)Поскольку математическое ожидание
- 11. Элементы планирования экспериментов
- 12. Счетная камера Горяева (гемацитометер)
- 13. Клетки в камере Горяева
- 14. Как подсчитывать клетки в камере ГоряеваN ±
- 15. Так сколько же клеток надо подсчитать, чтобы
- 16. Молитва и сепсис
- 17. Leonard Leibovici, Университет Тель-Авива, ИзраильОсновные научные интересы: Бактериальные инфекции и антибиотикотерапия;Компьютеризация медицинских исследований;Медицинская этика;Доказательная медицина.
- 18. Leonard Leibovici Effects of remote, retroactive intercessory
- 19. Основные характеристики двух групп пациентов
- 20. РезультатыСвязь между молитвой и смертностью от сепсиса
- 21. Основные меры эффекта в таблицах 2х2Разность долей
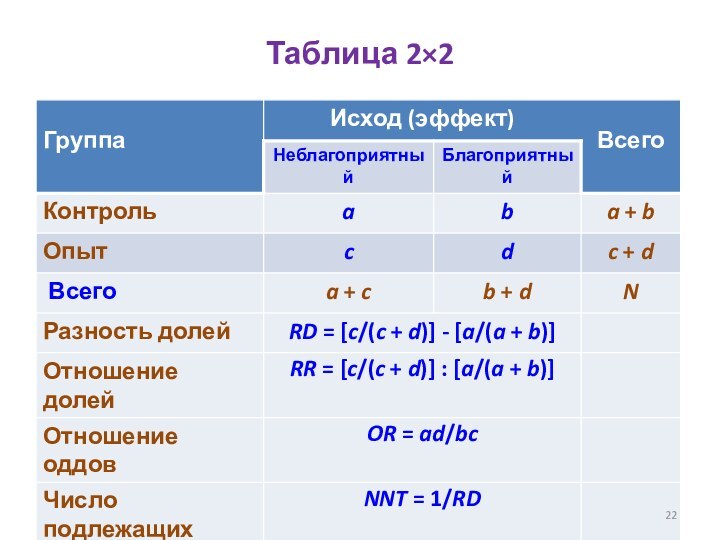
- 22. Таблица 2×2
- 23. Принципы построения бейзовских статистических оценок
- 24. Бейзовский Доверительный (правдоподобный) Интервал (ДИ)
- 25. Использованные программыМоделирование подбрасывания монет:http://www.random.org/coins/иhttp://www.random.org/coins/Построение графиков бета-распределения:http://keisan.casio.com/has10/SpecExec.cgiВычисление бейзовских доверительных интервалов для долей:Программа LePAC version 2.0.38http://www.univ-rouen.fr/LMRS/Persopage/Lecoutre/PAC.htmиhttp://www.causascientia.org/math_stat/ProportionCI.html
- 26. Порождение распределения для доли выпадения орлов φ(H) Нет информацииBeta(a* = 1, b* = 1)
- 27. Точечные и интервальные статистические оценки доли выпадения
- 28. Точечные и интервальные статистические оценки доли выпадения
- 29. Точечные и интервальные статистические оценки доли выпадения
- 30. Оценка доли скончавшихся в контрольной группе, φ1 в программе LePAC http://www.univ-rouen.fr/LMRS/Persopage/Lecoutre/PAC.htm
- 31. Плотность распределения и 99,9%-й ДИ для оцениваемой доли скончавшихся в контрольной группе, φ1φ1 = 0,270,300,34
- 32. Оценка доли скончавшихся в группе подвергнутых воздействию молитвы φ2 в программе LePAC
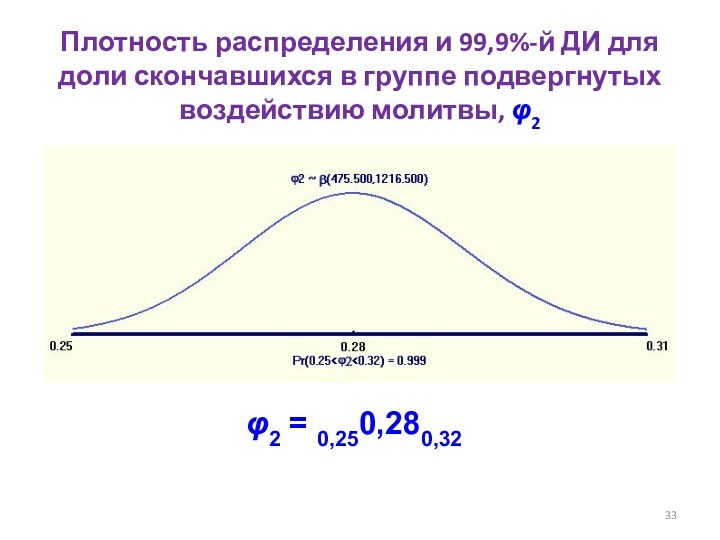
- 33. Плотность распределения и 99,9%-й ДИ для доли
- 34. Плотности распределения для долей скончавшихся от сепсиса
- 35. Оценка неизвестной разности долей RDunkn = δ = φ1 - φ2 в программе LePAC
- 36. Плотность распределения и 95%-й ДИ для оцениваемой
- 37. Плотность распределения для оцениваемой разности долей δ
- 38. 95%, 99% и 99,9% ДИ для оцениваемой
- 39. Что такое отношение рисков, RR = τ
- 40. Оценка неизвестного отношения долей (рисков) RRunkn = τ = φ1 / φ2 в программе LePAC
- 41. Плотность распределения и 95%-й ДИ для оцениваемого
- 42. 95%, 99% и 99,9% ДИ для оцениваемого
- 43. Что такое «отношение шансов», OR?Это «трехэтажное» отношение:1.
- 44. Оценка неизвестного отношения оддов (шансов за/против)
- 45. Плотность распределения и 95%-й ДИ для оцениваемого
- 46. 95%, 99% и 99,9% ДИ для оцениваемого
- 47. РезультатыСмертность в опытной группе была примерно на
- 48. Что такое NNT – количество подлежащих
- 49. Прочувствуйте разницуУтверждение: «необходимо подвергнуть данному воздействию 50
- 50. Относительные меры эффекта OR, RR, часто приводят
- 51. Программа Visual Rx http://www.nntonline.net/visualrx/
- 52. Верхняя граница ДИ для NNT - неопределенная
- 53. Вербальные шкалы
- 54. Надежность доверительных интервалов (ДИ)
- 55. Возможные словесные интерпретации для градаций Se и Sp
- 56. Возможные словесные интерпретации для градаций PPV и NPV
- 57. Принятые словесные интерпретации для градаций LR[+] и LR[-]
- 58. Словесные интерпретации для градаций AUC
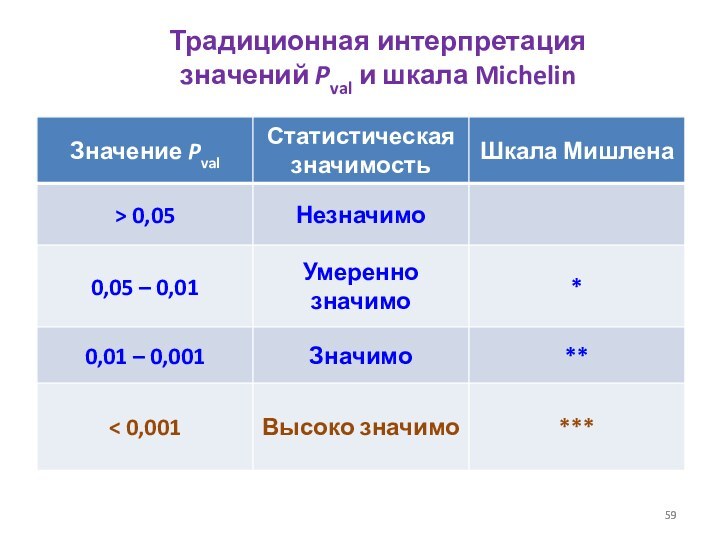
- 59. Традиционная интерпретация значений Pval и шкала Michelin
- 60. Калибровка Р-значений Для наглядности значения в таблице
- 61. Интерпретация убедительности Бейзовых факторов, BF10 и BF01
- 62. Интерпретация стандартизированного размера эффекта по Коуэну dC http://www.sportsci.org/resource/stats/
- 63. Словесная интерпретация для градаций модуля разности долей |RD| и для числа субъектов, подлежащих воздействию NNT
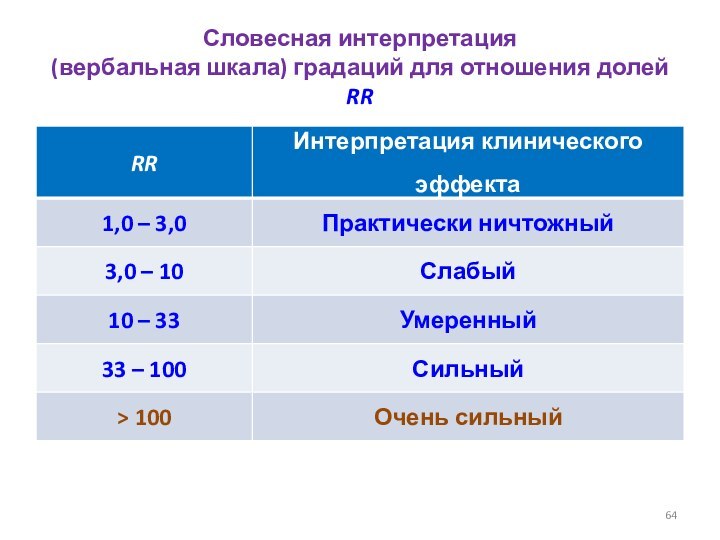
- 64. Словесная интерпретация (вербальная шкала) градаций для отношения долей RR
- 65. Словесная интерпретация (вербальная шкала) градаций для отношения шансов OR
- 66. Скачать презентацию
- 67. Похожие презентации






















































![Статистика в клеточной биологии и в клинических исследованиях Принятые словесные интерпретации для градаций LR[+] и LR[-]](/img/tmb/15/1414752/0afdfa6649306d6d54ace06e3bac01fe-720x.jpg)







Слайд 2
Упорядоченный посев и пуассонер –
высокоточная техника количественной микробиологии
МЕДИЦИНА.
XXI ВЕК
Слайд 3
Распределение Пуассона
Распределение числа событий, происходящих в фиксированном временнóм
или пространственном интервале (объеме),
при условии,
что эти события
независимы и чтовероятность совпадения (попадания в одну точку пространства) или одновременного наступления двух и более событий пренебрежимо мала.
Симеон Дени Пуассон (Siméon Denis Poisson, 21.06.1781—25.04.1840)
Слайд 4
Распределение Пуассона
P(k) = e-λλk/k!
e = 2,71828 – основание
натурального логарифма
k! = 1·2·…(k-1)·k – факториал
Характеристическое свойство раcпределения Пуассона
– его математическое ожидание (среднее значение) и дисперсия равны друг другу:Ek* = Dk* = λ,
т.е. это распределение имеет всего лишь один параметр λ.
Слайд 5
Пуассонер, упорядоченный посев
Н. Н. Хромов-Борисов, Jenifer Saffi ,
Joao A. P. Henriques Упорядоченный посев и пуассонер – высокоточная техника
количественной микробиологииСлайд 8 Распределения числа колоний дрожжей на десяти чашках Петри,
порожденные пуассонером, и их сравнение с распределением числа колоний,
полученных традиционным методом посева.
Слайд 10
Среднеквадратичное отклонение
(стандартная ошибка среднего)
Поскольку математическое ожидание (среднее значение)
и дисперсия распределения Пуассона равны друг другу:
Ek* = Dk*
= λ,то его среднеквадратичное отклонение есть:
SE = √Dk* = √λ
Слайд 14
Как подсчитывать клетки в камере Горяева
N ± √N
Сколько
клеток надо подсчитать, чтобы относительная ошибка составила 5%?
Ответ: ~
400Решение:
SE = √400 = 20
20 : 400 = 0,05
Слайд 15
Так сколько же клеток надо подсчитать, чтобы относительная
ошибка составила 1%?
Ответ: ~ 10 000
Решение:
SE = √10 000
= 100100 : 10 000 = 0,01
Слайд 17
Leonard Leibovici, Университет Тель-Авива, Израиль
Основные научные интересы:
Бактериальные
инфекции и антибиотикотерапия;
Компьютеризация медицинских исследований;
Медицинская этика;
Доказательная медицина.
Слайд 18 Leonard Leibovici Effects of remote, retroactive intercessory prayer
on outcomes in patients with bloodstream infection: randomised controlled trial
// BMJ, 2001. – Vol. 323. – P. 1450-1451.Методы
Выборку из 3393 пациентов с заражением крови (с сепсисом) рандомизированно, т.е. случайным образом разбили на две группы – контрольную (1702 пациента) и опытную (1691 пациент).
Перечень имен пациентов во второй группе был передан человеку, который произносил краткую молитву за улучшение здоровья и полное выздоровление всей этой группы целиком.
Пациенты, за которых молились, об этом не знали.
Слайд 20
Результаты
Связь между молитвой и смертностью от сепсиса статистически
незначима (Pval = 0,19 > 0,05). Полученное значение бейзова
фактора (BF01 = 12,7) показывает, что примерно в 13 раз более правдоподобно получить такие данные, когда эта связь действительно отсутствует, чем когда она есть. Молитва, скорее всего, не влияет на смертность при сепсисе.
Слайд 21
Основные меры эффекта в таблицах 2х2
Разность долей (рисков)
– RD (Risk Difference)
Отношение рисков (долей) – RR (Risk
Ratio)Отношение оддов (шансов за/против) – OR (Odds Ratio)
Число подлежащих воздействию – NNT (Number Needed to Treat)
Слайд 25
Использованные программы
Моделирование подбрасывания монет:
http://www.random.org/coins/
и
http://www.random.org/coins/
Построение графиков бета-распределения:
http://keisan.casio.com/has10/SpecExec.cgi
Вычисление бейзовских доверительных
интервалов для долей:
Программа LePAC version 2.0.38
http://www.univ-rouen.fr/LMRS/Persopage/Lecoutre/PAC.htm
и
http://www.causascientia.org/math_stat/ProportionCI.html
Слайд 27 Точечные и интервальные статистические оценки доли выпадения орлов
φ(H)
3 H : 7 T; n = 10 Beta(a*
= 4, b* = 8)Плотность бета распределения
Beta(a = 4, b = 8)
Слайд 28 Точечные и интервальные статистические оценки доли выпадения орлов
φ(H)
47 H : 53 T; n = 100; Beta(a*
= 48, b* = 54)527 H : 473 T; n=1000; Beta(a* = 528, b* = 474)
Слайд 29 Точечные и интервальные статистические оценки доли выпадения орлов
φ(H)
5111 H : 4889 T; n = 10 000;
Beta(a*
= 5112, b* = 4890)Более тонкий масштаб
Слайд 30 Оценка доли скончавшихся в контрольной группе, φ1 в
программе LePAC
http://www.univ-rouen.fr/LMRS/Persopage/Lecoutre/PAC.htm
Слайд 31 Плотность распределения и 99,9%-й ДИ для оцениваемой доли
скончавшихся в контрольной группе, φ1
φ1 = 0,270,300,34
Слайд 33 Плотность распределения и 99,9%-й ДИ для доли скончавшихся
в группе подвергнутых воздействию молитвы, φ2
φ2 = 0,250,280,32
Слайд 34 Плотности распределения для долей скончавшихся от сепсиса в
группах пациентов, подвернутых (φ1) и не подвергнутых молитве (φ2)
Слайд 36 Плотность распределения и 95%-й ДИ для оцениваемой разности
долей RDunkn = δ = φ1 - φ2
RD =
-0,0090,0210,052Слайд 37 Плотность распределения для оцениваемой разности долей δ =
φ1 - φ2 = RD в допустимых границах от
-1 до +1Слайд 38 95%, 99% и 99,9% ДИ для оцениваемой разности
долей RDunkn = δ = φ1 - φ2
Когда
доли равны (φ1 = φ2) , то их разность равна нулю: RD = δ = φ1 - φ2 = 0. Все три полученных ДИ для оцениваемой разности долей RDunkn содержат значение RD = 0.
Это дает нам основание утверждать, что, скорее всего, оцениваемое этими интервалами неизвестное нам значение RDunkn статистически не отличается от нуля и, соответственно, первая и вторая доли статистически одинаковы.
Основной вывод: Молитва, скорее всего, не влияет на смертность при сепсисе.
Слайд 39
Что такое отношение рисков, RR = τ ?
Это
есть отношение двух условных вероятностей (долей), например, доли скончавшихся
в контрольной группе φ1 к доле скончавшихся в опытной группе φ2:RR = φ1 / φ2
Слайд 41 Плотность распределения и 95%-й ДИ для оцениваемого отношения
долей (рисков) RRunkn = τ = φ1 / φ2
RR
= 0,971,081,19Слайд 42 95%, 99% и 99,9% ДИ для оцениваемого отношения
долей RRunkn = τ = φ1 / φ2
Когда доли
равны (φ1 = φ2), то их отношение равно единице: RR = τ = φ1 / φ2 = 1.
Все три полученных ДИ для оцениваемого отношения долей RRunkn содержат значение RR = 1.
Это дает нам основание утверждать, что, скорее всего, оцениваемое этими интервалами неизвестное нам значение RRunkn статистически не отличается от 1, соответственно, первая и вторая доли статистически одинаковы.
Основной вывод: Молитва, скорее всего, не влияет на смертность при сепсисе.
Слайд 43
Что такое «отношение шансов», OR?
Это «трехэтажное» отношение:
1. Вероятность
есть отношение количества исходов k, благоприятствующих данному событию (A)
к общему количеству исходов N:P(A) = k / N
2. Шансы (Odds) суть ставки за и против, т. е. отношение вероятности данного события P(A) к вероятности противоположного события P(nonA) = 1 – P(A):
Odds = P(A) : [1 - P(A)] = k / (N – k)
3. Отношение шансов (OR – Odds Ratio) есть отношение шансов за и против события A к шансам за и против события B:
OR = {P(A) / [1 - P(A)]} : {P(B) / [1 - P(B)]}
Слайд 44 Оценка неизвестного отношения оддов (шансов за/против) ORunkn =
ω = [φ1 / (1 - φ1)] : [φ2
/ (1 - φ2)] в программе LePACСлайд 45 Плотность распределения и 95%-й ДИ для оцениваемого отношения
оддов (шансов за/против), ORunkn = ω = [φ1 /
(1 - φ1)] : [φ2 / (1 - φ2)]OR = 0,961,111,28
Слайд 46 95%, 99% и 99,9% ДИ для оцениваемого отношения
оддов (шансов за/против) OR = ω = [φ1 /
(1 - φ1)] : [φ2 / (1 - φ2)]Когда доли равны, то отношение оддов равно единице: OR = ω = [φ1 / (1 - φ1)] : [φ2 / (1 - φ2)] = 1.
Все три полученных ДИ для оцениваемого отношения оддов ORunkn содержат значение OR = 1.
Это дает нам основание утверждать, что, скорее всего, оцениваемое этими интервалами неизвестное нам значение ORunkn статистически не отличается от 1, соответственно, первая и вторая доли статистически одинаковы.
Основной вывод: Молитва, скорее всего, не влияет на смертность при сепсисе.
Слайд 47
Результаты
Смертность в опытной группе была примерно на 2%
ниже, чем в контрольной, однако наблюдаемое различие между долями
φ1 и φ2 является статистически незначимым, т.е. оказывается кажущимся.φ1 = 0,270,300,34
φ2 = 0,250,280,32
RD = δ = φ1 – φ2 = -0,0300,0210,072 содержит значение 0.
RR = τ = φ1 / φ2 = 0,901,071,28
OR = ω = [φ1(1- φ1)] / [φ2(1-φ2)] = 0,861,111,42 – оба содержат значение 1.
Слайд 48
Что такое NNT –
количество подлежащих воздействию?
NNT –
Number Needed to Treat
Среднее количество пациентов, которых надо подвергнуть
(данному) воздействию, дабы предотвратить один неблагоприятный исход (или получить один дополнительный благоприятный исход)
по сравнению с контрольной группой (без данного воздействия).
Слайд 49
Прочувствуйте разницу
Утверждение:
«необходимо подвергнуть данному воздействию 50 пациентов,
чтобы предотвратить один неблагоприятный исход»
информативнее и понятнее, нежели:
«данное воздействие
снижает риск неблагоприятного исхода на 0,02»
Слайд 50
Относительные меры эффекта OR, RR, часто приводят к
впечатляющим цифрам, даже когда абсолютные эффекты воздействия (RD) оказываются
малымиПримеры:
1. φ1 = 0,6; φ2 = 0,1; RR = 6; OR = 13,5;
RD = 0,5; NNT = 2
2. φ1 = 0,06; φ2 = 0,01; RR = 6; OR = 110,06; но
RD = 0,05 и NNT = 20
Слайд 60
Калибровка Р-значений
Для наглядности значения в таблице округлены
до первой значащей цифры. Более точно значения для P(H0)
(сверху вниз) равны 29%, 11% и 1,8%.Posavac E.J. Using p values to estimate the probability of statistically significant replication // Understanding Statistics, 2002. – Vol. 1. – No. 2. – P. 101-112.