Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Степенные функции

Содержание

“СТЕПЕННЫЕ ФУНКЦИИ”Степенная функция с нечетным натуральным показателем.Корень нечетной степени.Степенная функция с четным натуральным показателем.Корень четной степени.Конец роботы.
Степенные функции.Выполнила учитель математикиМОУ СОШ № 31 г КраснодараШеремета Ирина Викторовна. “СТЕПЕННЫЕ ФУНКЦИИ”Степенная функция с нечетным натуральным показателем.Корень нечетной степени.Степенная функция с четным Степенная функция с нечетным натуральным показателем.Это функция f(x) = xn, где n Степенная функция с нечетным натуральным показателем.Функция f(x) = x.Строится график функции – Степенная функция с нечетным натуральным показателем.Функция f(x) = x.График функции f(x) = Степенная функция с нечетным натуральным показателем.Функция f(x) = x.Функции f(x) = x Степенная функция с нечетным натуральным показателем.Функция f(x) = x.Вопрос: принадлежит ли точка Степенная функция с нечетным натуральным показателем.Функция f(x) = x.ВЕРНО!Точка А(-2, 2) не Степенная функция с нечетным натуральным показателем.Функция f(x) = x.НЕВЕРНО!Точка А(-2, 2) не Степенная функция с нечетным натуральным показателем.Функция f(x) = x.Вопрос: принадлежит ли точка Степенная функция с нечетным натуральным показателем.Функция f(x) = x.ВЕРНО!Точка B(0.5, 0.5) принадлежит Степенная функция с нечетным натуральным показателем.Функция f(x) = x.НЕВЕРНО!Точка B(0.5, 0.5) принадлежит Степенная функция с нечетным натуральным показателем.Функция f(x) = x3.Строится график функции – Степенная функция с нечетным натуральным показателем.Функция f(x) = x3.График функции у = Степенная функция с нечетным натуральным показателем.Функция f(x) = x3.Функции у = x3 Степенная функция с нечетным натуральным показателем.Функция f(x) = x3.f(-x) = -f(x) для Степенная функция с нечетным натуральным показателем.Функция f(x) = x3.Рассмотрим отрезок АВ.Точка 0 Степенная функция с нечетным натуральным показателем.Функция f(x) = x3.Сравним графики функций f(x) Степенная функция с нечетным натуральным показателем.Функции f(x) = xn c нечетным натуральным Корень нечетной степени.Это функция f(x) = nx, являющаяся обратной для функции у Корень нечетной степени.Функция f(x) = 3xРассмотрим функцию f(x) = x3.Функция x3 монотонна, Корень нечетной степени.Функция f(x) = 3xГрафик функции у = 3xполучается симметричным отображением Корень нечетной степени.Функция f(x) = 3xГрафик у = 3x пересекает биссектрису у Корень нечетной степени.f(x) = 2n+1x, nN.График функции у = 2n+1x, nN,получается симметричным Степенная функция с четным натуральным показателем.Функция f(x) = x2.Строится график функции – Степенная функция с четным натуральным показателем.Функция f(x) = x2.Функция f(x) = x2 Степенная функция с четным натуральным показателем.Функция f(x) = x2.f(-x) = f(x) для Степенная функция с четным натуральным показателем.Функция f(x) = x2.Рассмотрим отрезок АС, точка Степенная функция с четным натуральным показателем.Функция f(x) = x2.Сравним графики функций f(x) Степенная функция с четным натуральным показателем.Функция f(x) = x2.Сравним графики функцийf(x) = СПАСИБО ЗА ВНИМАНИЕ
Слайды презентации

Слайд 2 “СТЕПЕННЫЕ ФУНКЦИИ”

Степенная функция с нечетным натуральным показателем.

Корень нечетной

“СТЕПЕННЫЕ ФУНКЦИИ”Степенная функция с нечетным натуральным показателем.Корень нечетной степени.Степенная функция с

степени.

Степенная функция с четным натуральным показателем.

Корень четной степени.

Конец роботы.

Слайд 3 Степенная функция с нечетным натуральным показателем.
Это функция f(x)

Степенная функция с нечетным натуральным показателем.Это функция f(x) = xn, где

= xn, где n – нечетное натуральное число.
МЕНЮ CЛЕД. ВЫХОД

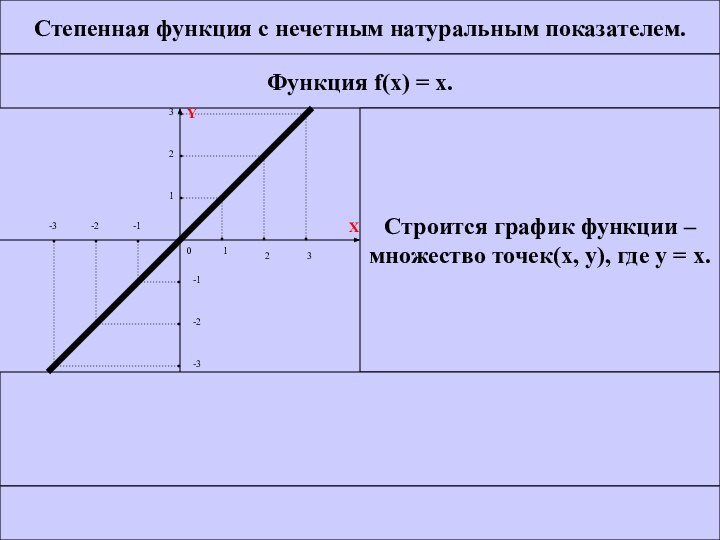
Слайд 4 Степенная функция с нечетным натуральным показателем.
Функция f(x) =

Степенная функция с нечетным натуральным показателем.Функция f(x) = x.Строится график функции

x.
Строится график функции –
множество точек(х, у), где у

= х.

МЕНЮ CЛЕД. ВЫХОД

-2

-3

-1

0

1

2

3

1

2

3

-1

-2

-3

Y

X

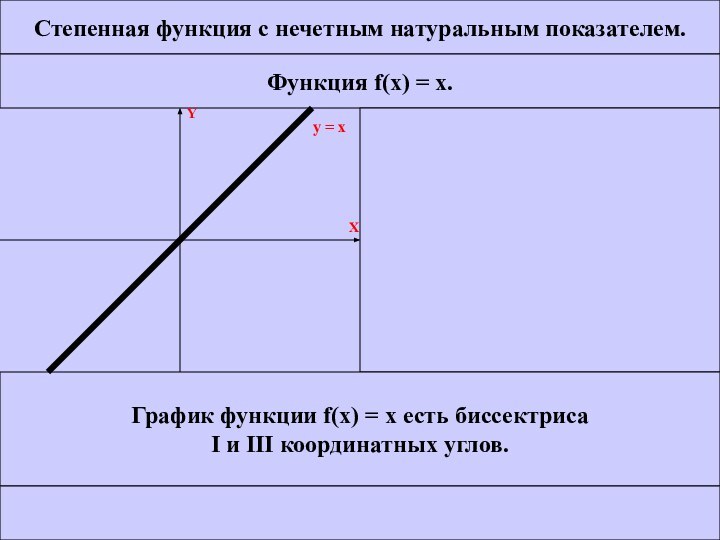
Слайд 5 Степенная функция с нечетным натуральным показателем.
Функция f(x) =

Степенная функция с нечетным натуральным показателем.Функция f(x) = x.График функции f(x)

x.
График функции f(x) = x есть биссектриса
I и

III координатных углов.

МЕНЮ CЛЕД. ВЫХОД

Y

X

y = x

Слайд 6 Степенная функция с нечетным натуральным показателем.
Функция f(x) =

Степенная функция с нечетным натуральным показателем.Функция f(x) = x.Функции f(x) =

x.
Функции f(x) = x определена на всем R,
непрерывна и

строго возрастает.

МЕНЮ CЛЕД. ВЫХОД

Y

X

y = x

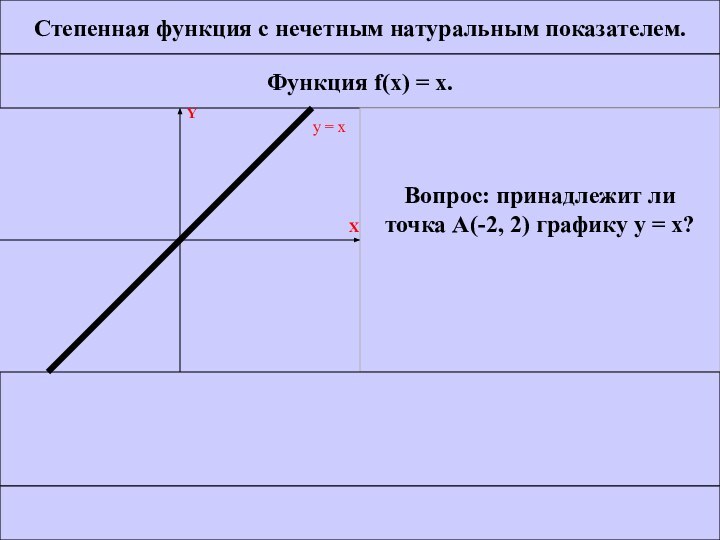
Слайд 7 Степенная функция с нечетным натуральным показателем.
Функция f(x) =

Степенная функция с нечетным натуральным показателем.Функция f(x) = x.Вопрос: принадлежит ли

x.
Вопрос: принадлежит ли
точка А(-2, 2) графику у =

х?

ДА НЕТ

МЕНЮ CЛЕД. ВЫХОД

Y

X

y = x

Слайд 8 Степенная функция с нечетным натуральным показателем.
Функция f(x) =

Степенная функция с нечетным натуральным показателем.Функция f(x) = x.ВЕРНО!Точка А(-2, 2)

x.
ВЕРНО!
Точка А(-2, 2) не принадлежит
графику у = х.


ДАЛЕЕ
МЕНЮ CЛЕД.

ВЫХОД

Y

X

y = x

А(-2, 2)

-2

2

Слайд 9 Степенная функция с нечетным натуральным показателем.
Функция f(x) =

Степенная функция с нечетным натуральным показателем.Функция f(x) = x.НЕВЕРНО!Точка А(-2, 2)

x.
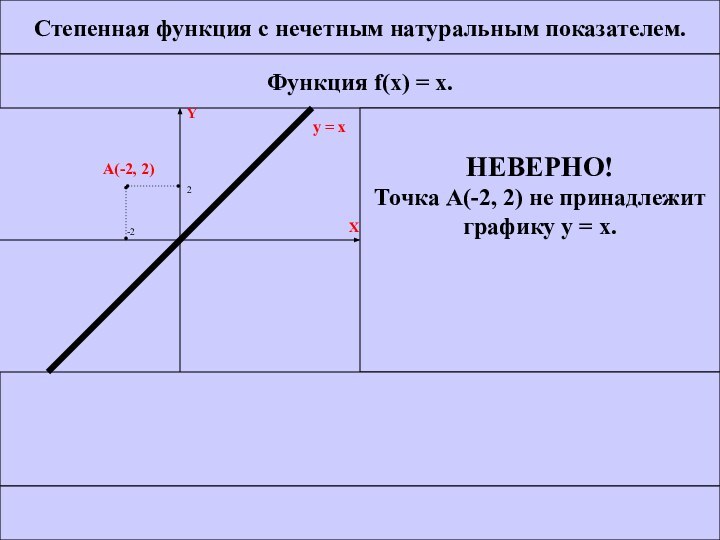
НЕВЕРНО!
Точка А(-2, 2) не принадлежит
графику у = х.


ДАЛЕЕ
МЕНЮ CЛЕД.

ВЫХОД

Y

X

y = x

А(-2, 2)

-2

2

Слайд 10 Степенная функция с нечетным натуральным показателем.
Функция f(x) =

Степенная функция с нечетным натуральным показателем.Функция f(x) = x.Вопрос: принадлежит ли

x.
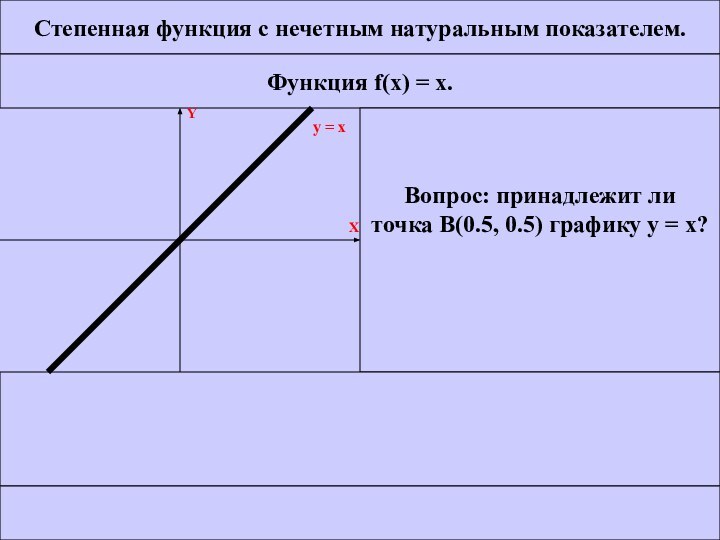
Вопрос: принадлежит ли
точка B(0.5, 0.5) графику у =

х?

ДА НЕТ

МЕНЮ CЛЕД. ВЫХОД

Y

X

y = x

Слайд 11 Степенная функция с нечетным натуральным показателем.
Функция f(x) =

Степенная функция с нечетным натуральным показателем.Функция f(x) = x.ВЕРНО!Точка B(0.5, 0.5)

x.
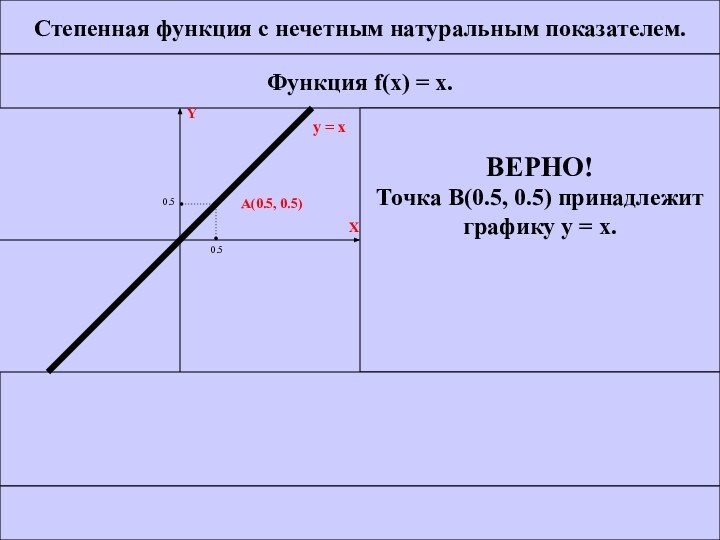
ВЕРНО!
Точка B(0.5, 0.5) принадлежит
графику у = х.


ДАЛЕЕ
МЕНЮ CЛЕД. ВЫХОД
Y
X
y

= x

А(0.5, 0.5)

0.5

0.5

Слайд 12 Степенная функция с нечетным натуральным показателем.
Функция f(x) =

Степенная функция с нечетным натуральным показателем.Функция f(x) = x.НЕВЕРНО!Точка B(0.5, 0.5)

x.
НЕВЕРНО!
Точка B(0.5, 0.5) принадлежит
графику у = х.


ДАЛЕЕ
МЕНЮ CЛЕД. ВЫХОД
Y
X
y

= x

А(0.5, 0.5)

0.5

0.5

Слайд 13 Степенная функция с нечетным натуральным показателем.
Функция f(x) =

Степенная функция с нечетным натуральным показателем.Функция f(x) = x3.Строится график функции

x3.
Строится график функции –
множество точек(х, у), где у

= x3.

МЕНЮ CЛЕД. ВЫХОД

Y

X

-3,375

-1

0

1

1,5

1

-1

-1,5

3,375

Слайд 14 Степенная функция с нечетным натуральным показателем.
Функция f(x) =

Степенная функция с нечетным натуральным показателем.Функция f(x) = x3.График функции у

x3.
График функции у = x3 называется
кубической параболой.
МЕНЮ CЛЕД. ВЫХОД
Y
X
0
y

= x3

Слайд 15 Степенная функция с нечетным натуральным показателем.
Функция f(x) =

Степенная функция с нечетным натуральным показателем.Функция f(x) = x3.Функции у =

x3.
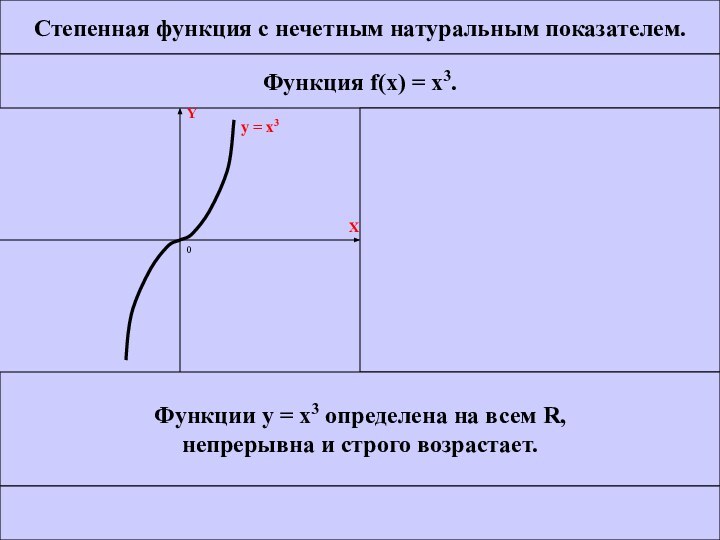
Функции у = x3 определена на всем R,
непрерывна и

строго возрастает.

МЕНЮ CЛЕД. ВЫХОД

Y

X

0

y = x3

Слайд 16 Степенная функция с нечетным натуральным показателем.
Функция f(x) =

Степенная функция с нечетным натуральным показателем.Функция f(x) = x3.f(-x) = -f(x)

x3.
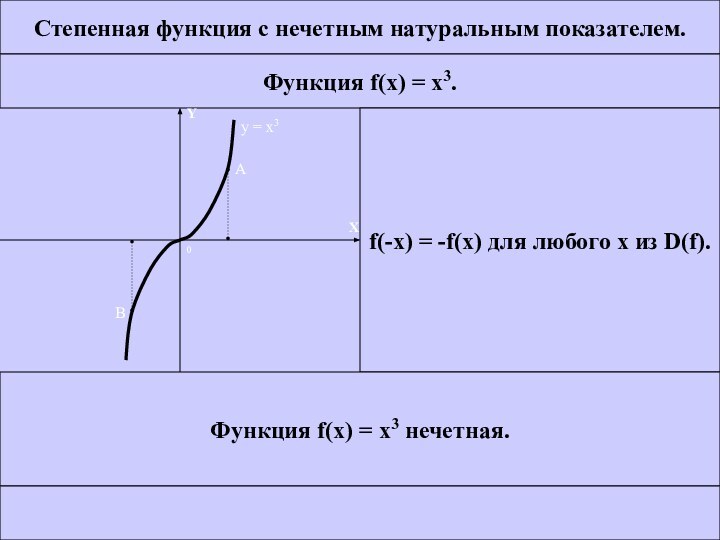
f(-x) = -f(x) для любого x из D(f).
Функция f(x)

= x3 нечетная.

МЕНЮ CЛЕД. ВЫХОД

Y

X

0

y = x3

А

В

Слайд 17 Степенная функция с нечетным натуральным показателем.
Функция f(x) =

Степенная функция с нечетным натуральным показателем.Функция f(x) = x3.Рассмотрим отрезок АВ.Точка

x3.
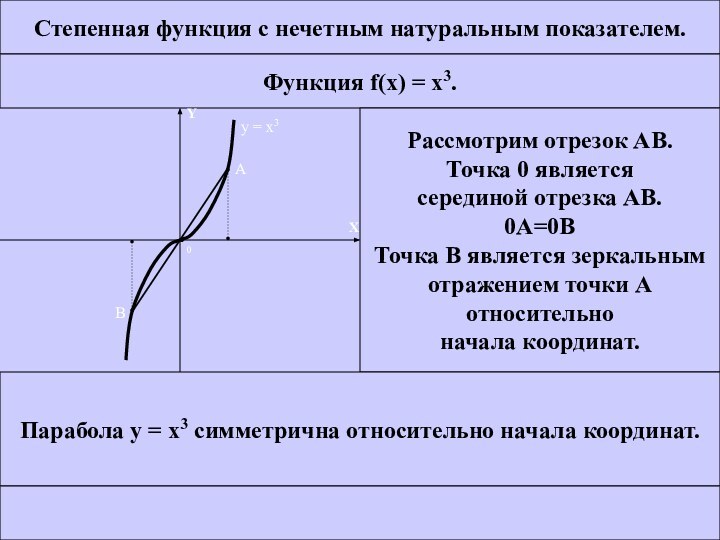
Рассмотрим отрезок АВ.
Точка 0 является
серединой отрезка АВ.
0А=0В
Точка В

является зеркальным
отражением точки А
относительно
начала координат.

Парабола у = х3 симметрична относительно начала координат.

МЕНЮ CЛЕД. ВЫХОД

Y

X

0

y = x3

А

В

Слайд 18 Степенная функция с нечетным натуральным показателем.
Функция f(x) =

Степенная функция с нечетным натуральным показателем.Функция f(x) = x3.Сравним графики функций

x3.
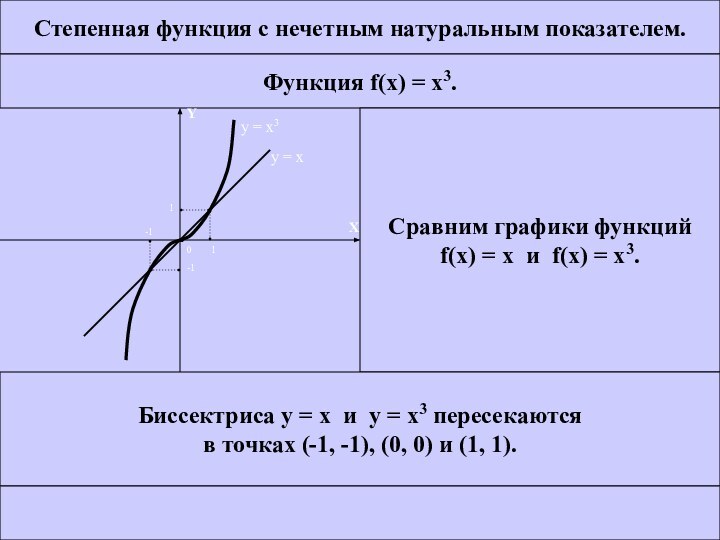
Сравним графики функций
f(x) = x и f(x) =

x3.

Биссектриса у = х и у = х3 пересекаются
в точках (-1, -1), (0, 0) и (1, 1).

МЕНЮ CЛЕД. ВЫХОД

Y

X

0

y = x3

-1

1

1

-1

y = x

Слайд 19 Степенная функция с нечетным натуральным показателем.
Функции f(x) =

Степенная функция с нечетным натуральным показателем.Функции f(x) = xn c нечетным

xn c нечетным натуральным показателем.
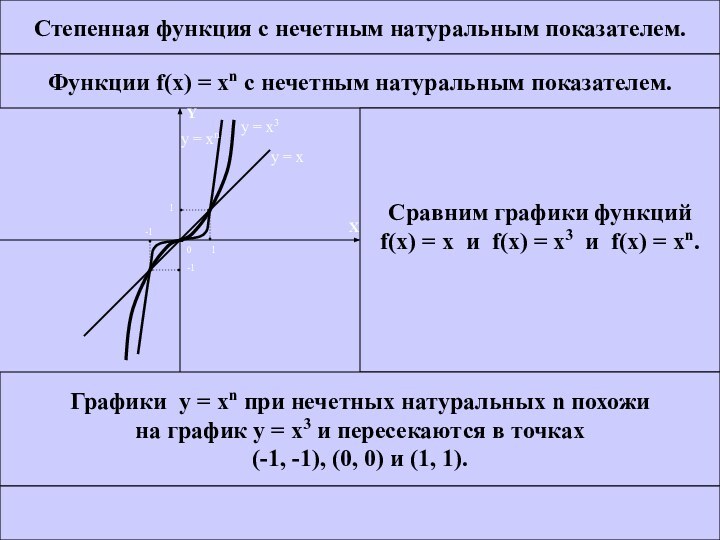
Сравним графики функций
f(x) =

x и f(x) = x3 и f(x) = xn.

Графики у = хn при нечетных натуральных n похожи
на график у = х3 и пересекаются в точках
(-1, -1), (0, 0) и (1, 1).

МЕНЮ CЛЕД. ВЫХОД

Y

X

0

y = x3

-1

1

1

-1

y = x

y = xn

Слайд 20 Корень нечетной степени.
Это функция f(x) = nx, являющаяся

Корень нечетной степени.Это функция f(x) = nx, являющаяся обратной для функции

обратной
для функции у = хn, где n нечетное

натуральное число, n>3.

МЕНЮ ПРЕД. CЛЕД. ВЫХОД

Слайд 21 Корень нечетной степени.
Функция f(x) = 3x
Рассмотрим функцию f(x)

Корень нечетной степени.Функция f(x) = 3xРассмотрим функцию f(x) = x3.Функция x3

= x3.
Функция x3 монотонна, поэтому имеет
обратную функцию 3x

(кубический корень из х).

МЕНЮ ПРЕД. CЛЕД. ВЫХОД

Y

X

0

y = x3

Слайд 22 Корень нечетной степени.
Функция f(x) = 3x
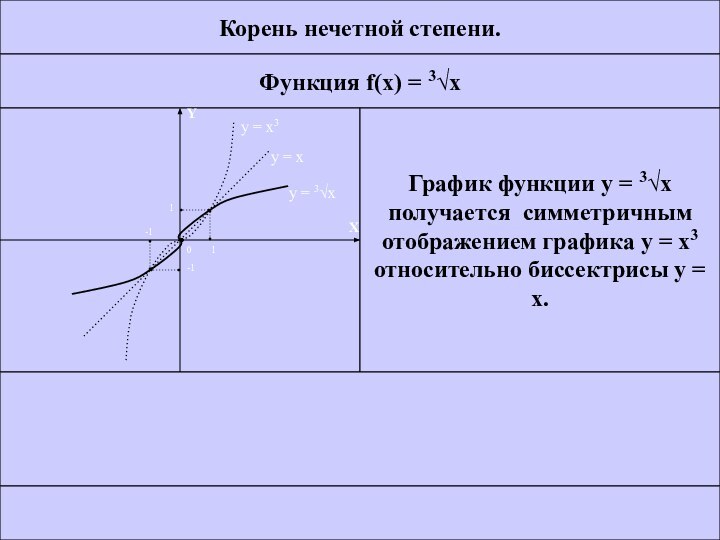
График функции у

Корень нечетной степени.Функция f(x) = 3xГрафик функции у = 3xполучается симметричным

= 3x
получается симметричным
отображением графика у = x3
относительно биссектрисы

у = x.

МЕНЮ ПРЕД. CЛЕД. ВЫХОД

Y

X

0

y = x3

y = x

-1

1

1

-1

y = 3x

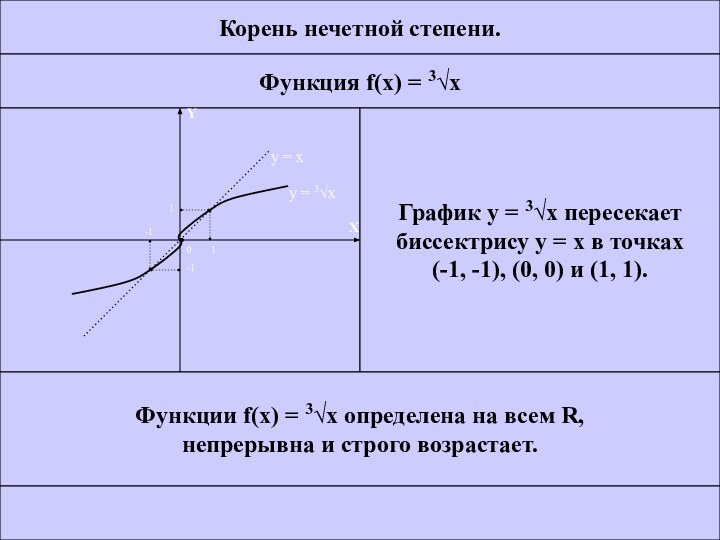
Слайд 23 Корень нечетной степени.
Функция f(x) = 3x
График у =

Корень нечетной степени.Функция f(x) = 3xГрафик у = 3x пересекает биссектрису

3x пересекает
биссектрису у = х в точках
(-1, -1),

(0, 0) и (1, 1).

Функции f(x) = 3x определена на всем R,
непрерывна и строго возрастает.

МЕНЮ ПРЕД. CЛЕД. ВЫХОД

Y

X

0

y = x

-1

1

1

-1

y = 3x

Слайд 24 Корень нечетной степени.
f(x) = 2n+1x, nN.
График функции у

Корень нечетной степени.f(x) = 2n+1x, nN.График функции у = 2n+1x, nN,получается

= 2n+1x, nN,
получается симметричным
отображением относительно
прямой у =

х графика
соответствующей функции
у = x2n+1.

Графики у = 2n+1x, nN, n>1, похожи на график
у = 3  х и пересекаются в точках (-1, -1), (0, 0) и (1, 1).

МЕНЮ ПРЕД. CЛЕД. ВЫХОД

Y

X

0

y = x

-1

1

1

-1

y = 3x

y = kx

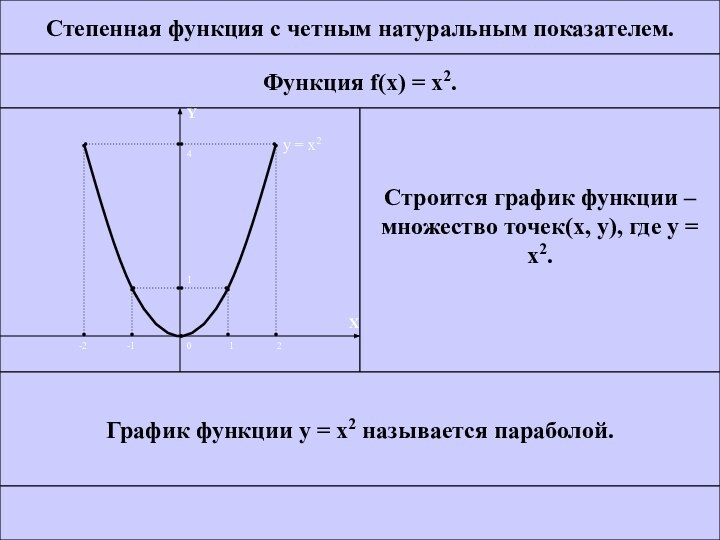
Слайд 25 Степенная функция с четным натуральным показателем.
Функция f(x) =

Степенная функция с четным натуральным показателем.Функция f(x) = x2.Строится график функции

x2.
Строится график функции –
множество точек(х, у), где у

= x2.

График функции у = x2 называется параболой.

МЕНЮ ПРЕД. ВЫХОД

Y

X

0

-1

1

2

-2

1

4

y = x2

Слайд 26 Степенная функция с четным натуральным показателем.
Функция f(x) =

Степенная функция с четным натуральным показателем.Функция f(x) = x2.Функция f(x) =

x2.
Функция f(x) = x2 определена на всем R, непрерывна,


строго убывает на (-OO, 0] и строго возрастает на [0, +OO).

МЕНЮ ПРЕД. ВЫХОД

Y

X

y = x2

0

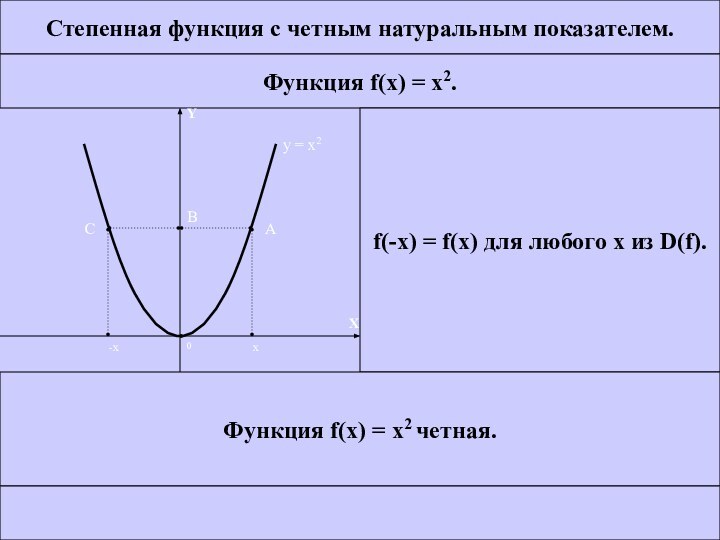
Слайд 27 Степенная функция с четным натуральным показателем.
Функция f(x) =

Степенная функция с четным натуральным показателем.Функция f(x) = x2.f(-x) = f(x)

x2.
f(-x) = f(x) для любого x из D(f).
Функция f(x)

= x2 четная.

МЕНЮ ПРЕД. ВЫХОД

Y

X

y = x2

0

A

C

B

-x

x

Слайд 28 Степенная функция с четным натуральным показателем.
Функция f(x) =

Степенная функция с четным натуральным показателем.Функция f(x) = x2.Рассмотрим отрезок АС,

x2.
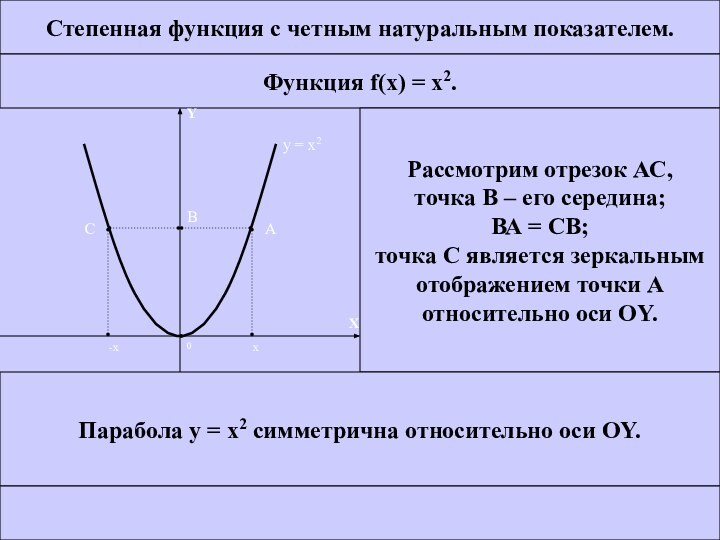
Рассмотрим отрезок АС,
точка В – его середина;
ВА =

СВ;
точка С является зеркальным
отображением точки А
относительно оси OY.

Парабола у = x2 симметрична относительно оси OY.

МЕНЮ ПРЕД. ВЫХОД

Y

X

y = x2

0

A

C

B

-x

x

Слайд 29 Степенная функция с четным натуральным показателем.
Функция f(x) =

Степенная функция с четным натуральным показателем.Функция f(x) = x2.Сравним графики функций

x2.
Сравним графики функций
f(x) = x и f(x) =

x2.

Биссектриса у = x и парабола у = x2
пересекаются в точках (0, 0) и (1, 1).

МЕНЮ ПРЕД. ВЫХОД

Y

X

y = x2

0

1

1

y = x

Слайд 30 Степенная функция с четным натуральным показателем.
Функция f(x) =

Степенная функция с четным натуральным показателем.Функция f(x) = x2.Сравним графики функцийf(x)

x2.
Сравним графики функций
f(x) = x2 и f(x) = x2k.


Графики

у = х2k k N. похожи
на график у = х2 и пересекаются в точках
(-1, 1), (0, 0) и (1, 1).

МЕНЮ ПРЕД. ВЫХОД

Y

X

y = x2

0

1

1

y = x

-1

y = x2k

  • Имя файла: stepennye-funktsii.pptx
  • Количество просмотров: 293
  • Количество скачиваний: 0
- Предыдущая Повторим информатику
Следующая - Каковы были цели России в составе Антанты?

Похожие презентации

Тайны теоремы Пифагора Тайны теоремы Пифагора 116
Презентация к предметной неделе Презентация к предметной неделе 107
Векторы Векторы 128
Презентация. Интерактивная игра Сосчитай рыбок Презентация. Интерактивная игра Сосчитай рыбок 110
Решение задач на прямую и обратную пропорциональные зависимости Решение задач на прямую и обратную пропорциональные зависимости 108
Экологическое воспитание через урок математики Экологическое воспитание через урок математики 99
Урок-путешествие по математике Урок-путешествие по математике 101
Презентация к уроку математики в 3 классе.Устный счёт Думай, считай, рассуждай! презентация к уроку по математике (3 класс) Презентация к уроку математики в 3 классе.Устный счёт Думай, считай, рассуждай! презентация к уроку по математике (3 класс) 122
Презентация к уроку по математике 5 класс на тему Площадь прямоугольника. Презентация к уроку по математике 5 класс на тему Площадь прямоугольника. 139
Равнобедренная трапеция. Признаки, свойства, интересные факты. Равнобедренная трапеция. Признаки, свойства, интересные факты. 115
Устный счёт. Математика 3 класс. презентация урока для интерактивной доски (математика, 3 класс) по теме Устный счёт. Математика 3 класс. презентация урока для интерактивной доски (математика, 3 класс) по теме 59
Презентация по математике Производная и её применение в алгебре,геометрии Презентация по математике Производная и её применение в алгебре,геометрии 127
Математика сабағына арналған сыныптан тыс шара Шахматы математик слайд Математика сабағына арналған сыныптан тыс шара Шахматы математик слайд 168
Как построить график функции y=f(x+L)+m, если известен график функции y=f(x) Как построить график функции y=f(x+L)+m, если известен график функции y=f(x) 138
Презентация по математике на тему Цилиндр,конус и шар (6 класс) Презентация по математике на тему Цилиндр,конус и шар (6 класс) 160
Умножение положительных и отрицательных чисел Умножение положительных и отрицательных чисел 113
Конспект занятия-путешествия c использованием интерактивной доски Цветик- семицветик для детей старшего возраста. методическая разработка по математике (старшая группа) Конспект занятия-путешествия c использованием интерактивной доски Цветик- семицветик для детей старшего возраста. методическая разработка по математике (старшая группа) 91
Приложение производной в школьном курсе математики Приложение производной в школьном курсе математики 100
Прямая, отрезок, луч, угол Прямая, отрезок, луч, угол 88
Решение задач с помощью уравнения Решение задач с помощью уравнения 118
Теория бесконечных множеств. Часть 2 Теория бесконечных множеств. Часть 2 84
Отчёт по самообразованию Активизация познавательного интереса на уроках математики учебно-методический материал по математике Отчёт по самообразованию Активизация познавательного интереса на уроках математики учебно-методический материал по математике 158
Тригонометрические уравнения Тригонометрические уравнения 117
Весёлая геометрия Весёлая геометрия 88
Прогулка на луг методическая разработка по математике (подготовительная группа) Прогулка на луг методическая разработка по математике (подготовительная группа) 165
Презентация Свойства действий с рациональными числами Презентация Свойства действий с рациональными числами 117
Исследовательская работа на уроках математики Исследовательская работа на уроках математики 107
Презентация Способы решения задач презентация к уроку по математике (3 класс) Презентация Способы решения задач презентация к уроку по математике (3 класс) 65
Учим математике играя! ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ презентация по математике Учим математике играя! ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ презентация по математике 104
Математика в специальности Товароведение и экспертиза качества потребительских товаров Математика в специальности Товароведение и экспертиза качества потребительских товаров 93