- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Стратегия построения курсов обучения математике : принципы обучения математике
Содержание
- 2. ПланПринципы обучения - как фундамент построения образовательного
- 3. Стратегия – искусство планирования руководства чем-либо, основанного
- 4. Обучение математике – управление процессом формирования и
- 5. Принципы в педагогике и дидактикеПринципы обучения –
- 6. Принципы обучения – фундамент построения любого образовательного процесса, в том числе и обучения математике.
- 7. Примеры систем принципов обученияЮ.К. БабанскийНаучностьСвязь с жизньюСистематичность
- 8. Иерархические системы принципов, отражающие целевые требования
- 9. Характеристика отдельных принциповПринцип выделения главного трактуется как
- 10. Характеристика отдельных принциповПринцип деятельности раскрывает механизм реализации
- 11. Характеристика отдельных принциповПринцип преемственности обучения – предполагает
- 12. Характеристика отдельных принциповПринцип психологической комфортности – предполагает
- 13. Характеристика отдельных принциповПринцип творчества – предполагает максимальную
- 14. Общие особенности построения современных систем принципов
- 15. Специфические принципы построения курсов математикигенерализации знаний (выделение
- 16. Сущность некоторых принципов обучения математике с
- 17. Сущность некоторых принципов обучения математике с позиции
- 18. Сущность некоторых принципов обучения математике с позиции
- 19. Сущность некоторых принципов обучения математике с позиции
- 20. Сущность некоторых принципов обучения математике с позиции
- 21. Сущность некоторых принципов обучения математике с позиции
- 22. Сущность некоторых принципов обучения математике с позиции
- 23. Сущность некоторых принципов обучения математике с позиции
- 24. Сущность некоторых принципов обучения математике с позиции
- 25. Сущность некоторых принципов обучения математике с позиции
- 26. Сущность некоторых принципов обучения математике с позиции
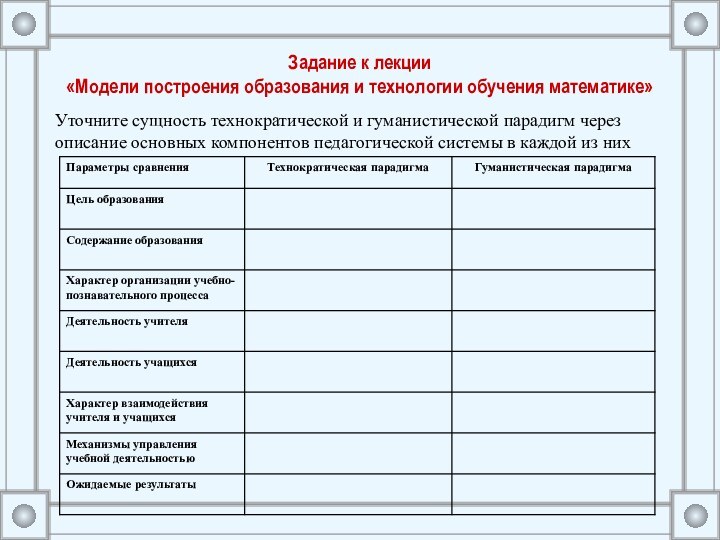
- 27. Задание к лекции «Модели построения образования и
- 28. Скачать презентацию
- 29. Похожие презентации
ПланПринципы обучения - как фундамент построения образовательного процесса.Различные подходы к построению системы принципов обучения.Специфика некоторых принципов обучения математике с позиции современной образовательной парадигмы.



























Слайд 2
План
Принципы обучения - как фундамент построения образовательного процесса.
Различные
подходы к построению системы принципов обучения.
математике с позиции современной образовательной парадигмы.Слайд 3 Стратегия – искусство планирования руководства чем-либо, основанного на
правильных и далеко идущих прогнозах.
Стратегия – общие, основные установки,
важные для подготовки и осуществления чего-либо.Слайд 4 Обучение математике – управление процессом формирования и накопления
соответствующих когнитивных (умственных) структур учащихся.
Основные руководящие идеи, нормативные требования
к содержанию, организации и методам обучения сформулированы в принципах обучения
Слайд 5
Принципы в педагогике и дидактике
Принципы обучения – система
основных дидактических требований к процессу обучения, соблюдение которых обеспечивает
эффективное и качественное развитие учебного процесса и достижение заявленных целей образования.Принципы обучения отражают общественные потребности и меняются в соответствии с изменениями в обществе:
с повышением требований к уровню подготовки специалистов;
с повышением требований к доминирующим качествам мыслительной деятельности человека;
с появлением нового менталитета и т.п.
Слайд 6 Принципы обучения – фундамент построения любого образовательного процесса,
в том числе и обучения математике.
Слайд 7
Примеры систем принципов обучения
Ю.К. Бабанский
Научность
Связь с жизнью
Систематичность и
последовательность
Доступность
Сознательность и активность
Наглядность
Т.А. Ильин
Наглядность
Сознательность и активность
Доступность
Научность
Учет возрастных и индивидуальных
особенностейСистематичности и последовательности
Прочности
Связи с жизнью
И.П. Подласый
Сознательность и активность
Наглядность
Системность и последовательность
Прочность
Научность
Доступность
Связь теории с практикой
В.А. Оганесян
Развивающего и воспитывающего обучения
Научности и доступности
Систематичности и последовательности
Связи обучения с жизнью
Слайд 8 Иерархические системы принципов, отражающие целевые требования к построению
современного обучения математике
И.Д. Пехлецкий
Выделения главного
Учета возрастных
и индивидуальных особенностей Сознательности и активности
Самостоятельности
Доступности
Наглядности
Систематичности и последовательности
Научности
Практичности
Л.А. Леонтьев
Деятельности
Целостности представлений о мире
Непрерывности (преемственности)
Минимакса
Психологической комфортности
Вариативности
Творчества
Слайд 9
Характеристика отдельных принципов
Принцип выделения главного трактуется как принцип
целепологания на педагогическом, дидактическом, методическом уровне.
Этот принцип позволяет
осуществлять педагогически значимую технологию обучения и выделять эффективный предметный материал для достижения поставленной цели обучения и развития школьников.
Слайд 10
Характеристика отдельных принципов
Принцип деятельности раскрывает механизм реализации цели
и задач развивающего обучения и подразумевает включение каждого школьника
в учебно-познавательную деятельность, тесно связан с принципом сознательности, самостоятельности и активности обучения.Принцип целостного представления о мире – означает, что
у учащихся должно быть сформировано обобщённое
представление о мире (о природе, об обществе, о самом себе),
о роли и месте каждой науки в системе наук),
школьное знание должно отражать язык науки и не должно ей
противоречить, т.е. есть связь с принципами научности,
наглядности.
Слайд 11
Характеристика отдельных принципов
Принцип преемственности обучения – предполагает связь
между всеми ступенями обучения на уровне методологии, содержания и
методики, т.е. имеется связь с принципами систематичности и последовательности.Принцип минимакса – заключается в том, что школа обязана предложить ученику содержание образования по максимуму, а ученик обязан усвоить его на минимальном уровне, т.е. есть прямая связь с принципом доступности и принципом учета возрастных и индивидуальных возможностей.
Слайд 12
Характеристика отдельных принципов
Принцип психологической комфортности – предполагает учёт
особенностей законов развития психики, ориентирует на создание благоприятных условий
развития психической сферы ребёнка, т.е. связан с принципами доступности и учёта возрастных и индивидуальных особенностей.Принцип вариативности – предполагает:
ориентацию на развитие вариативности и комбинаторного
мышления,
понимание иного аспектного видения объекта и явлений,
формирование умения осуществлять системный перебор
вариантов и находить оптимальный вариант, т.е. связан
с принципами сознательности, последовательности,
активности.
Слайд 13
Характеристика отдельных принципов
Принцип творчества – предполагает максимальную ориентацию
на творческое начало учебной деятельности школьника, на приобретение им
собственного опыта творческой деятельности в школьные годыВ традиционно-классической системе принципов нет аналога данному принципу.
Слайд 14
Общие особенности построения
современных систем принципов
акценты значимости
расставляются в соответствии с конкретной исторической, культурной или социальной
заявкой;в конкретных условиях иерархия принципов определяется общей идеологией построения образовательного процесса с учетом особенностей личности учителя и обучаемых;
новые системы принципов могут строиться на основе комбинирования принципов разных систем или изменением их иерархии.
Слайд 15
Специфические принципы построения курсов математики
генерализации знаний (выделение стержней
курса);
внутрипредметных связи;
построения программы по спирали;
единства непрерывности и дискретности
обучения;обучения на социокультурном опыте;
гуманитарной направленности;
деятельностного подхода.
Слайд 16 Сущность некоторых принципов обучения математике с позиции
современной образовательной парадигмы
Принцип генерализации знаний
Начинать построение курса математики надо
с истоков, с выделения основных структур и понятий, организовывать математическое обучение в порядке развёртывания структур и понятий. Формировать не только отдельные знания и качества мышления, но и всю их структуру.
Раскрывать внутренние связи и отношения фундаментальных понятий. На конкретных фактах и явлениях показывать проявление этих понятий.
Располагать материал необходимо так, чтобы всё последующее вытекало из предыдущего, было развитием прежнего знания.
Слайд 17 Сущность некоторых принципов обучения математике с позиции современной
образовательной парадигмы
Генерализация знаний
связана с прочностью знаний учащихся об основных
изучаемых структурах;позволяет обеспечить лучшее понимание учащимися учебного материала;
позволяет на основных понятиях, как на стержнях, строить «скелет» математических знаний.
В современных курсах школьной математики в качестве идейного стержня часто выступает понятие математической модели реального процесса
Слайд 18 Сущность некоторых принципов обучения математике с позиции современной
образовательной парадигмы
Принцип внутрипредметных связей (выдвинут В.А. Далингером)
предполагает необходимость выделения
в современном курсе математики ведущих, общих понятий.ведущие понятия должны удовлетворять следующим критериям:
а) формировать у учащихся научное мировоззрение;
б) значительно чаще других понятий служить средством изучения различных вопросов математики;
в) активно работать на протяжении большого промежутка времени;
г) должны иметь прикладную, гуманитарную направленность;
д) должны способствовать реализации внутрипредметных и межпредметных связей.
Слайд 19 Сущность некоторых принципов обучения математике с позиции современной
образовательной парадигмы
Принцип построения программы по спирали
Предполагает нелинейное расположение
материала. Линейное расположение материала присутствует на небольших промежутках учебного времени ( от 2-х, 3-х месяцев до 2-х, 3-х лет). Целостность изучения объекта обеспечивается через интеграцию теоретического материала и практических умений в содержательно-методические линии.
Данный принцип является реализацией разумного сочетания научности и доступности обучения.
Слайд 20 Сущность некоторых принципов обучения математике с позиции современной
образовательной парадигмы
Научная строгость предполагает
непротиворечивость и логическую последовательность изложения
основ математики, использование общепринятых трактовок математических фактов, понятий, идей, апробированных практикой и позволяющих обобщать значительную группу фактов и явлений действительности,
не предполагает строгого, дедуктивного изложения курса школьной математики, а предполагает лишь демонстрацию дедуктивного характера математических знаний.
Слайд 21 Сущность некоторых принципов обучения математике с позиции современной
образовательной парадигмы
Принцип единства непрерывности и дискретности
Разделяется на две
взаимосвязанных части:преемственность обучения, отражающую непрерывность обучения;
многоступенчатость обучения, отражающую дискретность, этапность обучения.
Слайд 22 Сущность некоторых принципов обучения математике с позиции современной
образовательной парадигмы
Преемственность характеризуется опорой на изученное, то есть с
опорой на ЗУНы, которые получены на предыдущих ступенях обучения, с теми которые будут приобретены в будущем.Принцип преемственности требует выполнения следующих условий:
Обеспечение неразрывной связи между отдельными сторонами, этапами и ступенями обучения, и внутри них;
Расширение и углубление знаний, приобретенных на определенных этапах;
Преобразование отдельных представлений в стройную систему знаний, умений и навыков;
Поступательно-восходящий характер учебного процесса при обязательном учете качественного изменения учащихся.
Слайд 23 Сущность некоторых принципов обучения математике с позиции современной
образовательной парадигмы
Формы реализации преемственности
Понятия, которые рассматривались раньше, должны
сохраняться, но их содержание расширяется, уточняется, обобщается;Новые теоремы и целые теории либо строятся в рамках старых знаний, либо новые теории и идеи появляются, как обобщение ранее известных фактов;
Сохраняются методы при изменении содержания;
Сохраняется единой символики;
Осуществляется перенос знаний из одной области математики в другую;
Используются аналогии из ранее изученных теорий.
Слайд 24 Сущность некоторых принципов обучения математике с позиции современной
образовательной парадигмы
Обучение на социокультурном опыте
Наличие практической направленности обучения и
связи обучения с жизнью, которое не следует воспринимать упрощенно, то есть как насыщение занятия большим количеством примеров. Формирование понимания важности математических методов, логичности, строгости и того, что математика изучает не само явление, а его математическую модель.
Слайд 25 Сущность некоторых принципов обучения математике с позиции современной
образовательной парадигмы
Принцип гуманитарной направленности
Выделяются следующие составляющие гуманитарного потенциала
математики:несмотря на то, что математика имеет широкое применение в естествознание, она не относится к естественным наукам;
математика изучает не только развитие природы, но и законы развития общества, и законы мышления;
математика относится больше к гуманитарным наукам, так как является языком описания действительности;
в интеллектуальном развитии личности роль математики очень велика, так как ни один из школьных предметов не может конкурировать с ней в развитии мышления.
Слайд 26 Сущность некоторых принципов обучения математике с позиции современной
образовательной парадигмы
Принцип деятельностного подхода
Необходимость целенаправленной активной деятельности не
только учителя, но и учащегося;формирование необходимых качеств личности для осуществления полноценной деятельности, поэтому деятельности необходимо учить;
приоритет отдаётся формированию не узких видов математической деятельности, а формированию умений, навыков, интеллекта. Математическое содержание – это средство, с помощью которого достигаются эти задачи.