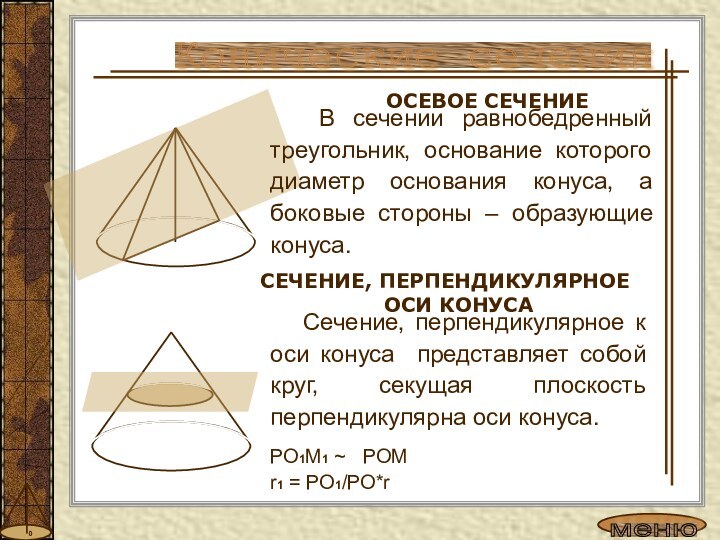
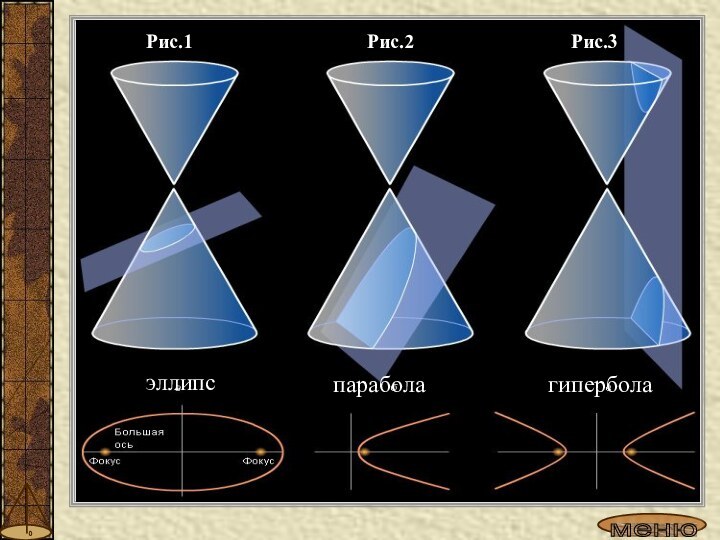
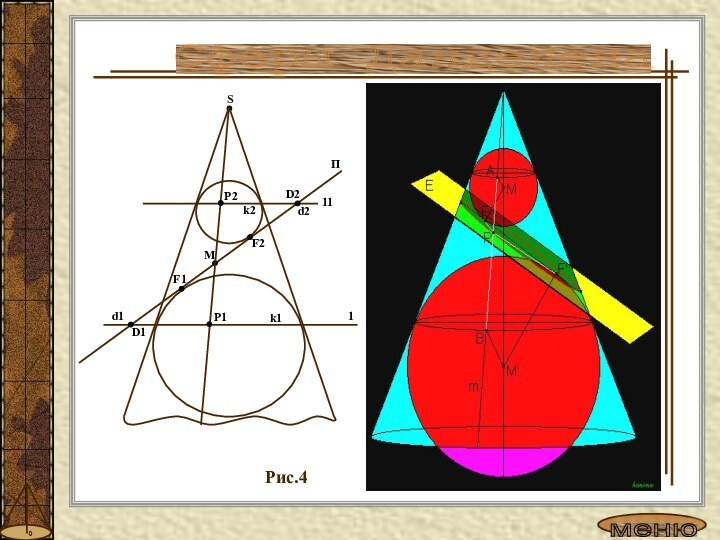
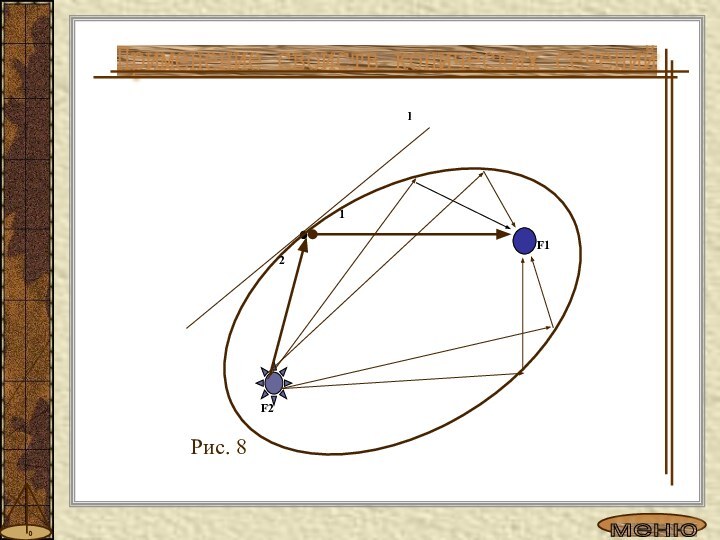
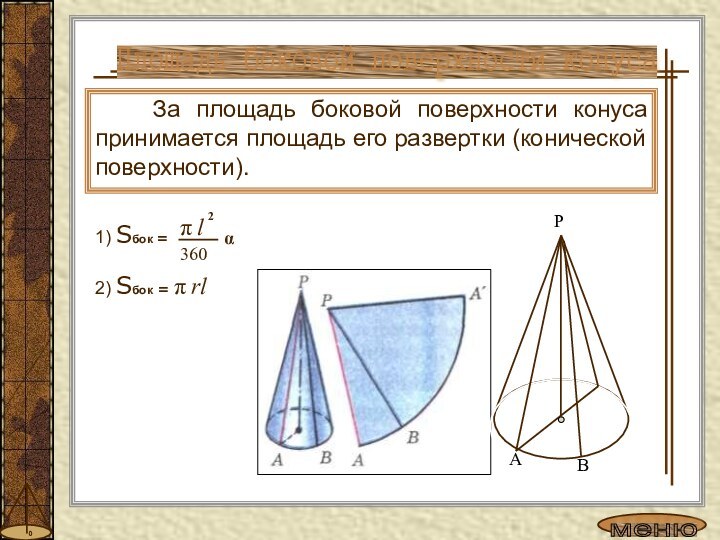
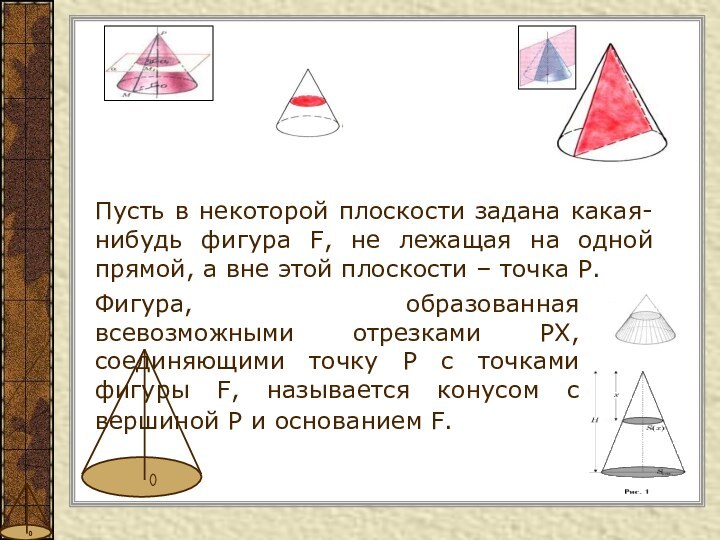
шишка».
С конусом люди знакомы с глубокой древности.
Много
сделала для геометрии школа Платона (428–348 гг. до н. э.). Школе Платона, в частности, принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса;
б) изучение конических сечений.
Историческая справка о конусе