- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Пифагора 2
Содержание
- 2. ПланВведениеБиография ПифагораПростейшее доказательство теоремыДревнекитайское доказательствоДоказательство ЕвклидаДоказательство теоремы ПифагораЕще одно алгебраическое доказательствоЕгипетский треугольникЗаключениеСписок литературыАвторы
- 3. ВведениеТрудно найти человека, у которого имя Пифагора
- 4. Биография Пифагора
- 5. Теорема ПифагораВ прямоугольном треугольникеквадрат гипотенузы равенсумме квадратов катетовc²=a²+b²
- 6. Простейшее доказательство “Квадрат,
- 7. Древнекитайское доказательство
- 8. Доказательство Евклида Дано: ∆АВС-прямоугольный, а,b-катеты, с-гипотенуза,
- 9. Доказательство теоремы ПифагораДано: треугольник АВС -
- 10. Еще одно алгебраическое доказательствоДано: ∆АВС – прямоугольный,
- 11. Пифагоровы треугольники Прямоугольные треугольники,
- 12. Египетский треугольник Землемеры Древнего
- 13. Заключение В заключении еще
- 14. АвторШевцова Наталья Александровна, учитель математики высшей категории
- 15. Скачать презентацию
- 16. Похожие презентации
ПланВведениеБиография ПифагораПростейшее доказательство теоремыДревнекитайское доказательствоДоказательство ЕвклидаДоказательство теоремы ПифагораЕще одно алгебраическое доказательствоЕгипетский треугольникЗаключениеСписок литературыАвторы














Слайд 2
План
Введение
Биография Пифагора
Простейшее доказательство теоремы
Древнекитайское доказательство
Доказательство Евклида
Доказательство теоремы Пифагора
Еще
одно алгебраическое доказательство
Слайд 3
Введение
Трудно найти человека, у которого имя Пифагора не
ассоциировалось бы с теоремой Пифагора. Пожалуй, даже те, кто
в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина: это простота — красота — значимость. Теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о гигантском числе ее конкретных реализаций.
Слайд 4
Биография Пифагора
Пифагор родился
около 570 г. до н.э. на острове Самосе.В юности Пифагор отправляется в Милет, где встречается с ученым
Фалесом, который советует ему отправится за знаниями в Египет. В
548 г. до н.э. Пифагор прибыл в самосскую колонию. Изучив язык и
религию египтян, он уезжает в Мемфис. Жрецы не спешили раскрывать Пифагору свои тайны, предлагая ему сложные испытания, но Пифагор преодолел их все. Научившись всему, что дали ему жрецы, он двинулся на родину в Элладу.
Однако, проделав часть пути, его захватил в плен царь Вавилона. Вавилонская математика была более развитой, чем египетская, и Пифагору было чему поучится, позже он сбежал на родину.
На родине Пифагор учредил нечто вроде религиозно-этического братства.
...Прошло 20 лет. Однажды к Пифагору приходит Килон, человек богатый, но злой, желая спьяну вступить в братство. Получив отказ, он поджигает дом Пифагора. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор покончил жизнь самоубийством.
Слайд 5
Теорема Пифагора
В прямоугольном треугольнике
квадрат гипотенузы равен
сумме квадратов катетов
c²=a²+b²
Слайд 6
Простейшее доказательство
“Квадрат, построенный
на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на
его катетах”Рассмотрим равнобедренный прямоугольный треугольник (с него и начиналась теорема).
Достаточно посмотреть на мозаику равнобедренных прямоугольных треугольников.
Для ABC квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, — по 2.
Слайд 7
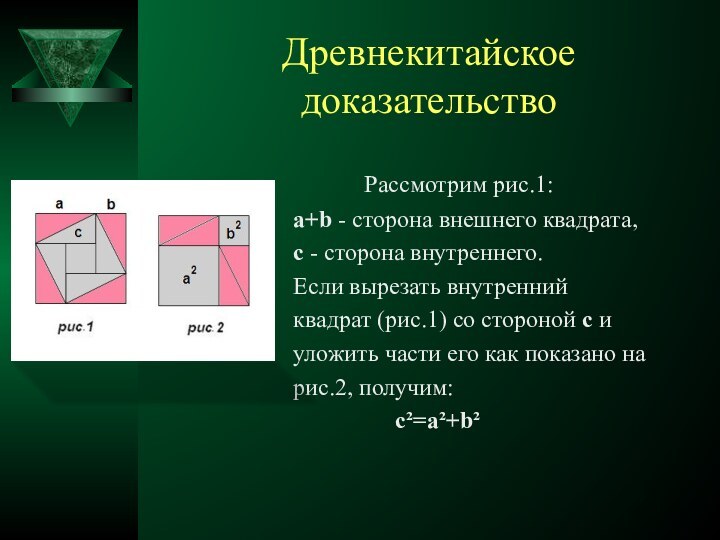
Древнекитайское доказательство
Рассмотрим
рис.1:
а+b - сторона внешнего квадрата,
с - сторона
внутреннего.Если вырезать внутренний
квадрат (рис.1) со стороной с и
уложить части его как показано на
рис.2, получим:
c²=a²+b²
Слайд 8
Доказательство Евклида
Дано: ∆АВС-прямоугольный, а,b-катеты, с-гипотенуза,
ABHF, AGKC, BCED-квадраты
Доказать: c²=a²+b²
Доказательство:
1. ∆ABD=∆FBC(по
2-м сторонам и углу м/у ними)BC=BD
FB=AB
∟DBА=90ْ +∟ABC=∟FBC
2. S∆ABD=1∕2SBYLD
BD- общее основание,
LD- общая высота
3. S∆FBC = 1∕2 SABFY (аналогично 2)
4. SABFH = SBYLD, т.к. ∆ABD=∆FBC
5. SACKG= SYCEL , т.к. ∆BCK=∆ACE(аналогично 1-4)
6. b²+a²=c² => c²=a²+b².
Слайд 9
Доказательство теоремы Пифагора
Дано: треугольник АВС -
прямоугольный
a, b - катеты
с-гипотенуза
Доказать: c2=a2+b2
Доказательство:
1. (a + b)2 = 4(1/2ab) + c2
2. a2 + 2ab + b2 = 2ab + c2
3. a2 + b2 = c2
Слайд 10
Еще одно алгебраическое доказательство
Дано: ∆АВС – прямоугольный, ∟С=90º
Доказать:
АС²+СВ²=АВ²
Доказательство:
1.CD-высота.
2. cosА=AD/AC=AC/AB =>AD∙AB=AC²
3. cosB=BD/BC=BC/AB =>AB∙BD=BC²
4. Получим :
AD∙AB+AB∙BD=AC²+BC²AB(AD+BD)=AC²+BC²
AB²=AC²+BC²
Слайд 11
Пифагоровы треугольники
Прямоугольные треугольники, у
которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками:
3, 4 и 55, 12 и 13
8, 15 и 17
7, 24 и 25
Слайд 12
Египетский треугольник
Землемеры Древнего Египта
для построения прямого угла пользовались следующим приемом.
Бечевку узлами делили на 12 равных частей и концы связывали. Затем бечевку растягивали на земле так, чтобы получался треугольник со сторонами 3, 4 и 5 делений.Угол треугольника, противолежащий стороне с 5 делениями, был прямой
(3²+4 ² =5 ²).





























