- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теория телетрафика
Содержание
- 2. АНАЛИТИЧЕСКИЕ МЕТОДЫ В ТЕОРИИ ТЕЛЕТРАФИКА Андрей Андреевич
- 3. ©КрыловВероятностная модель СМО дискретная цепь Маркова однородная
- 4. ©КрыловЦепи МарковаТеорема 1.Состояния неприводимой цепи Маркова либо
- 5. ©КрыловЦепи марковаДля неприводимой и апериодической цепи Маркова
- 6. ©КрыловЦепи МарковаСостояние называется эргодическим, если оно апериодично
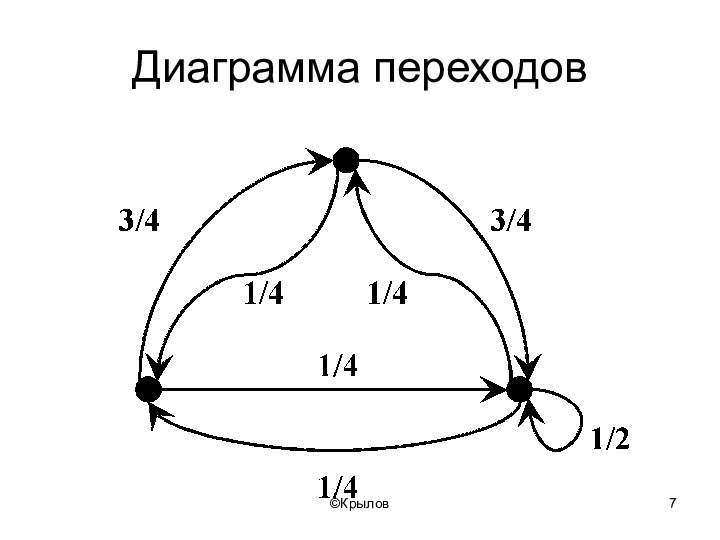
- 7. ©КрыловДиаграмма переходов
- 8. ©КрыловРешение примера
- 9. ©КрыловУравнения Чепмена-Колмогорова.(Chapman - Kolmogorov)
- 10. ©КрыловНепрерывные цепи Маркова Случайный процесс X(t)
- 11. ©КрыловНепрерывные цепи МарковаH(t) = [pij(t)] - матрица
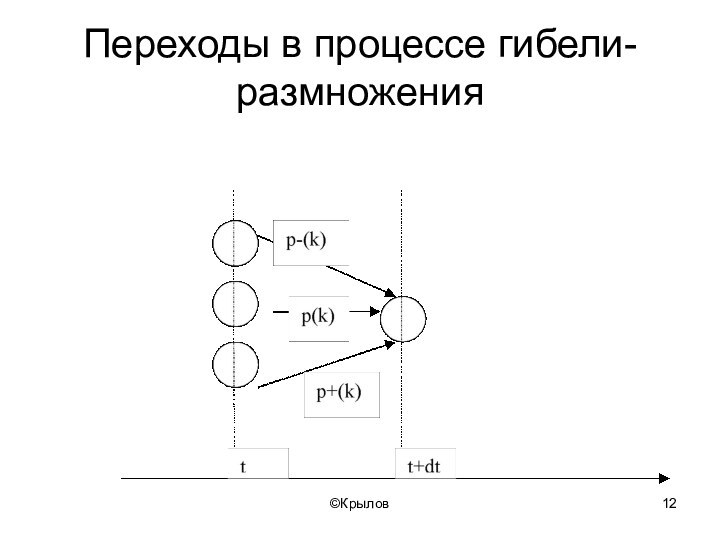
- 12. ©КрыловПереходы в процессе гибели-размножения
- 13. ©КрыловУравнения процесса гибели-размножения
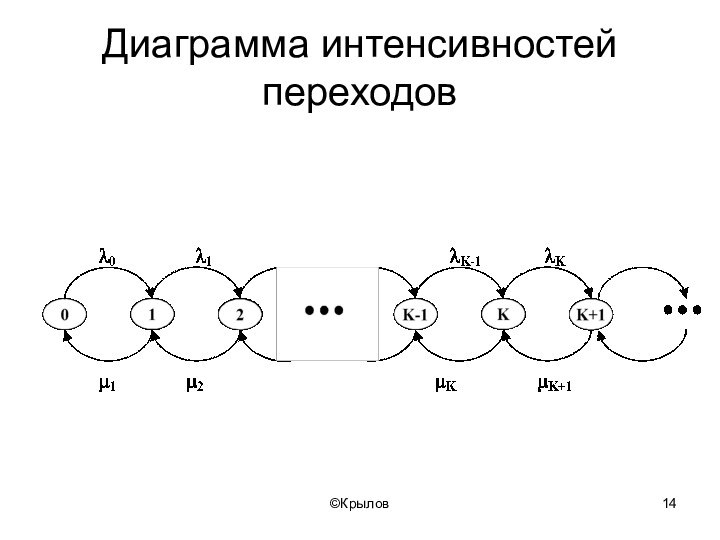
- 14. ©КрыловДиаграмма интенсивностей переходов
- 15. ©КрыловУравнения равновесия
- 16. ©КрыловРешение уравнений равновесия
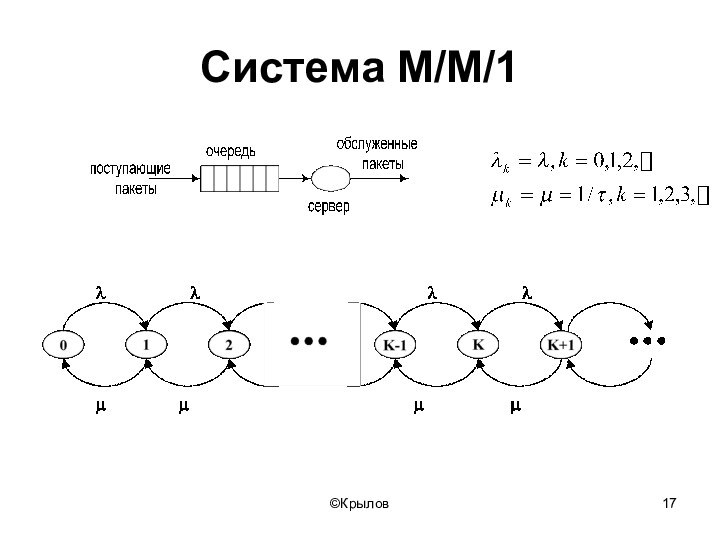
- 17. ©КрыловСистема M/M/1
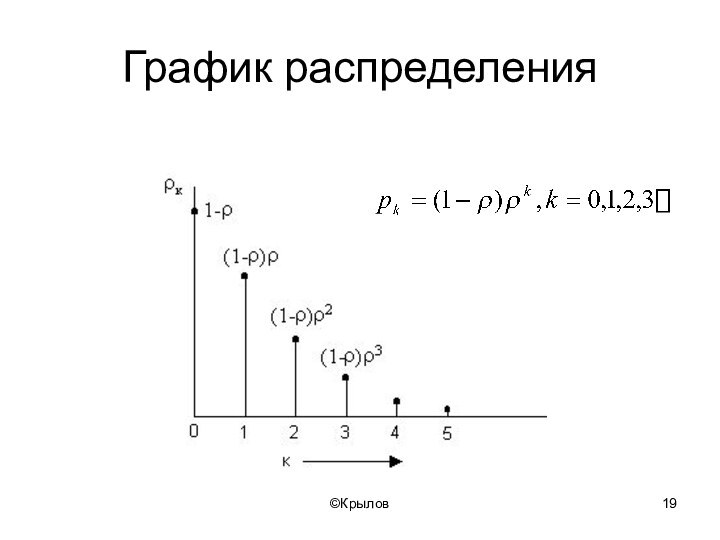
- 18. ©КрыловСтационарное распределение
- 19. ©КрыловГрафик распределения
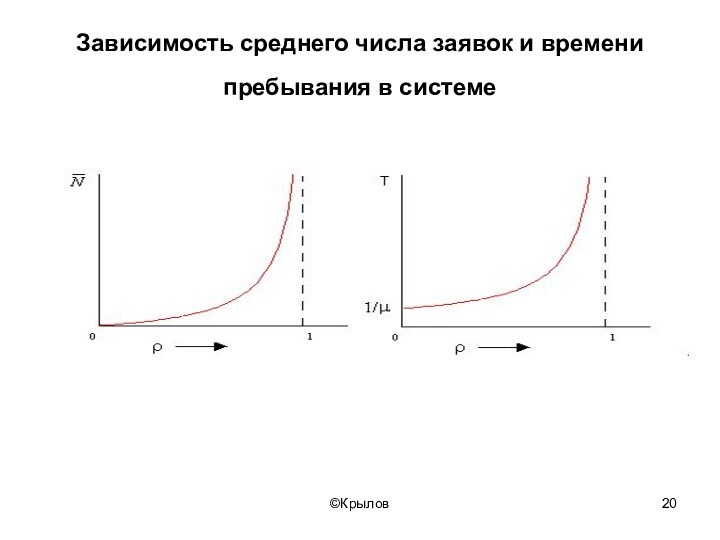
- 20. ©КрыловЗависимость среднего числа заявок и времени пребывания в системе
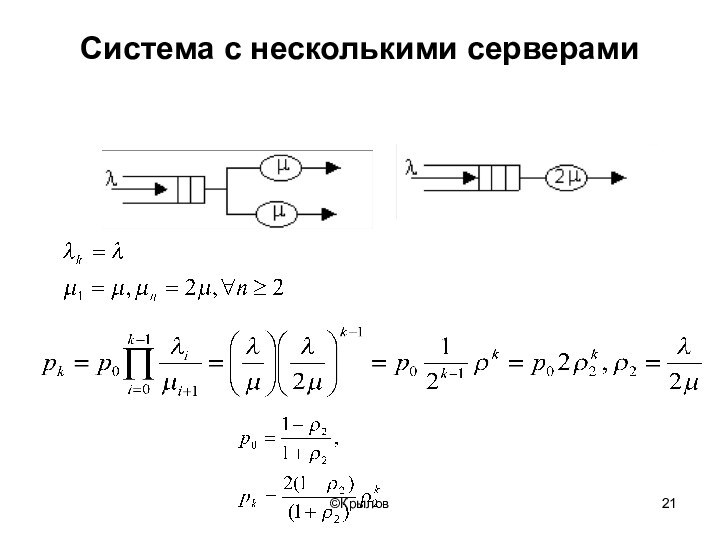
- 21. ©КрыловСистема с несколькими серверами
- 22. ©КрыловДвухсерверная система
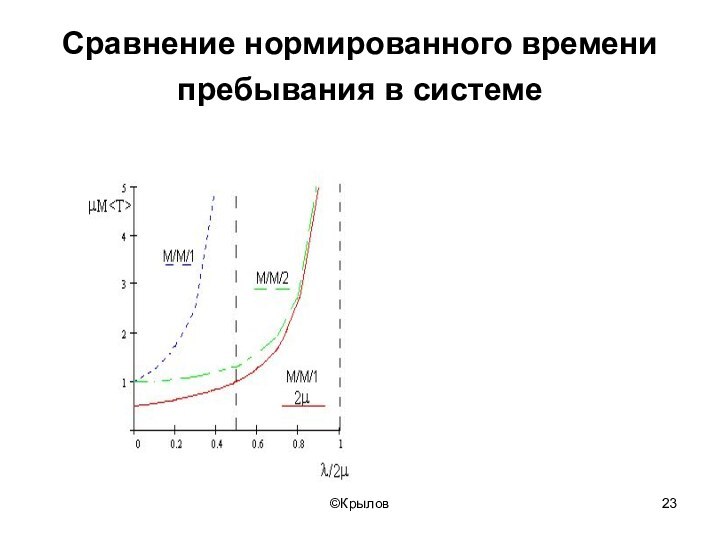
- 23. ©КрыловСравнение нормированного времени пребывания в системе
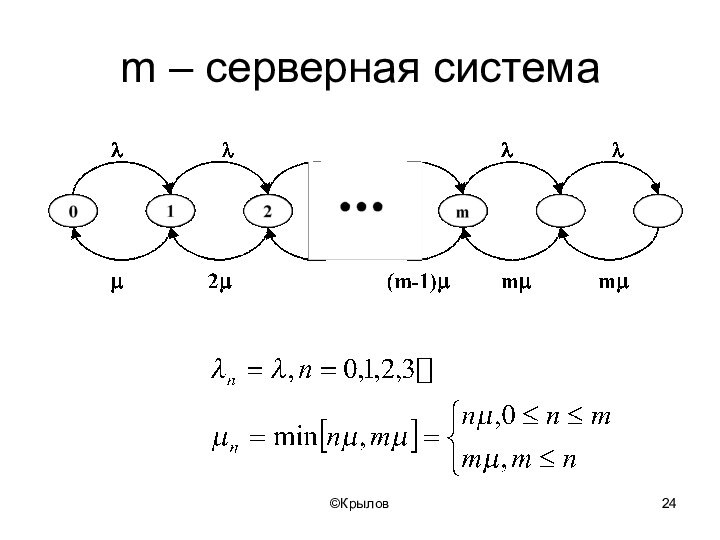
- 24. ©Крыловm – серверная система
- 25. ©Крыловm-cерверная система
- 26. ©КрыловС-формула Эрланга
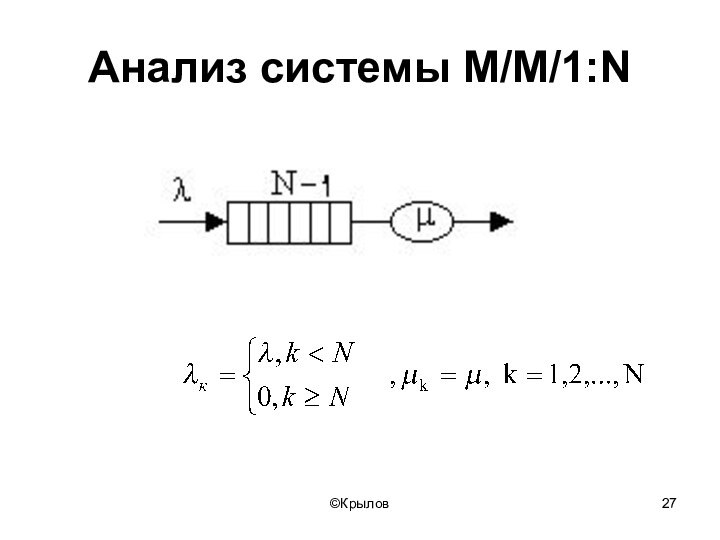
- 27. ©КрыловАнализ системы M/M/1:N
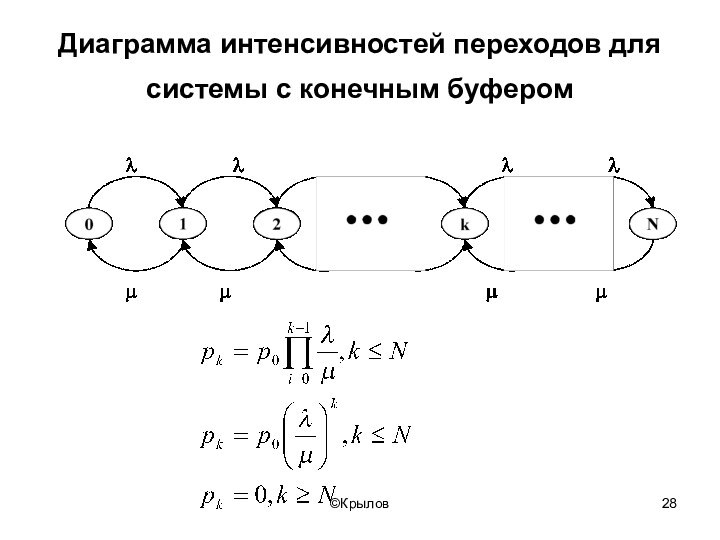
- 28. ©КрыловДиаграмма интенсивностей переходов для системы с конечным буфером
- 29. ©КрыловСтационарные вероятности
- 30. ©КрыловВероятность блокировки и пропускная способность
- 31. ©КрыловСредняя длина очереди и задержка в системе
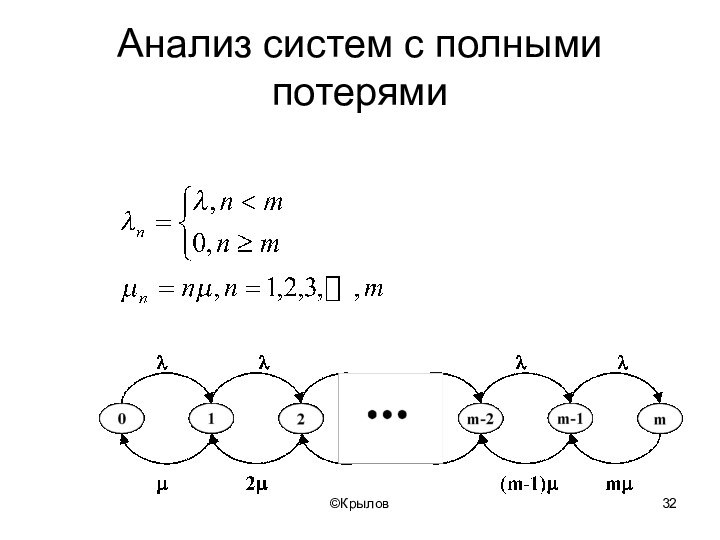
- 32. ©КрыловАнализ систем с полными потерями
- 33. ©КрыловСтационарные вероятности
- 34. ©КрыловВ-формула Эрланга
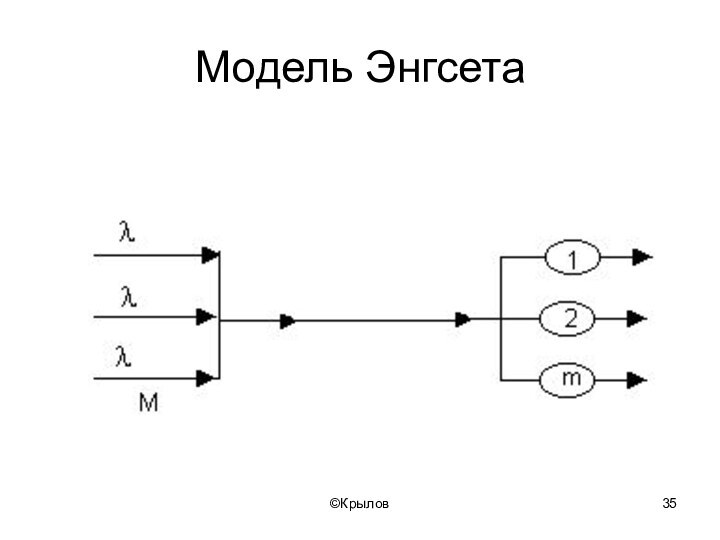
- 35. ©КрыловМодель Энгсета
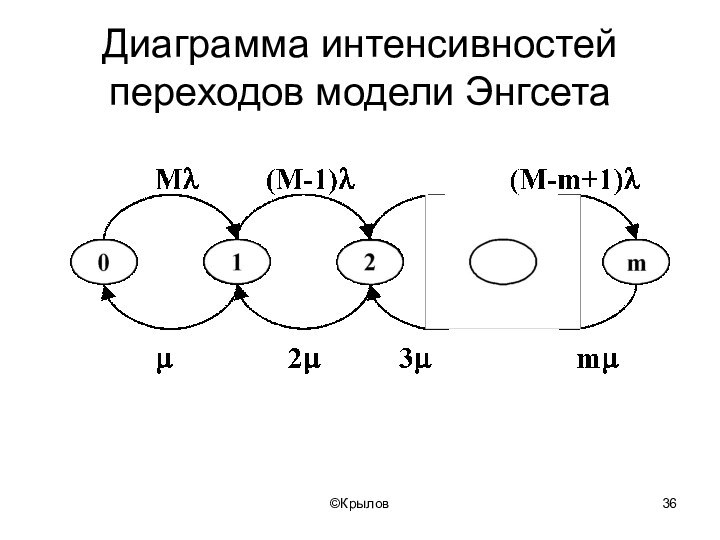
- 36. ©КрыловДиаграмма интенсивностей переходов модели Энгсета
- 37. ©КрыловПараметры и решение
- 38. ©КрыловСтационарные вероятности
- 39. ©КрыловФормула Энгсета
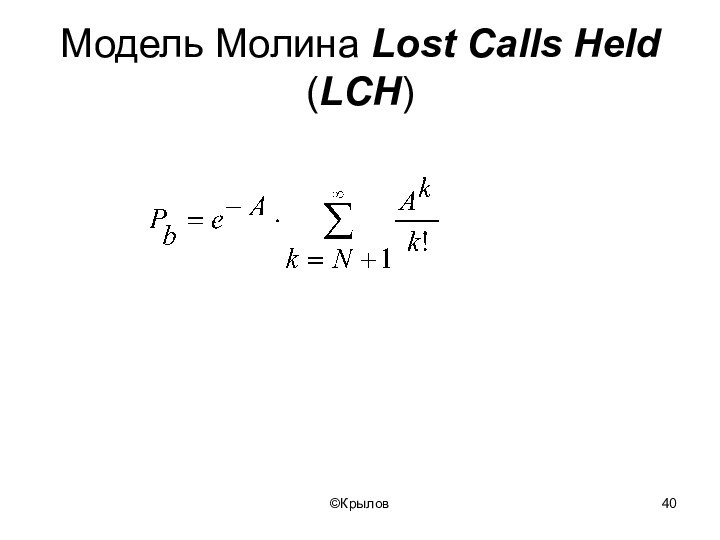
- 40. ©КрыловМодель Молина Lost Calls Held (LCH)
- 41. ©КрыловАнализ системы M/G/1
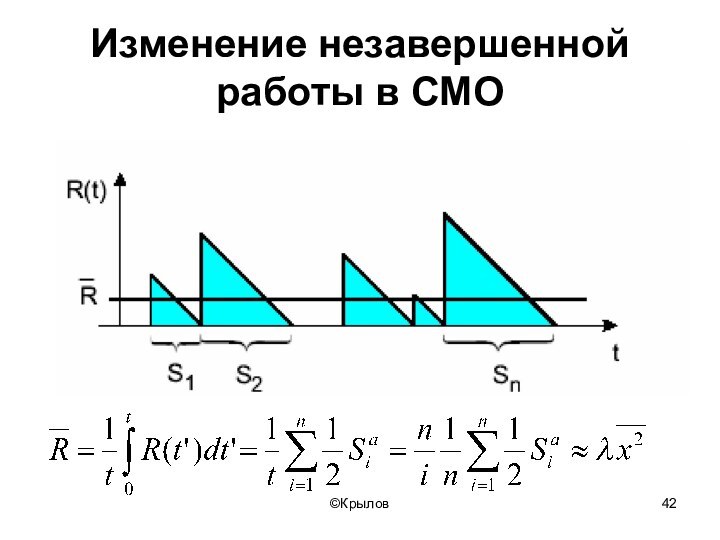
- 42. ©КрыловИзменение незавершенной работы в СМО
- 43. ©КрыловФормула Полячека-Хинчина
- 44. ©КрыловСреднее число требований
- 45. ©КрыловСистема M/M/1
- 46. ©КрыловСистема M/D/1
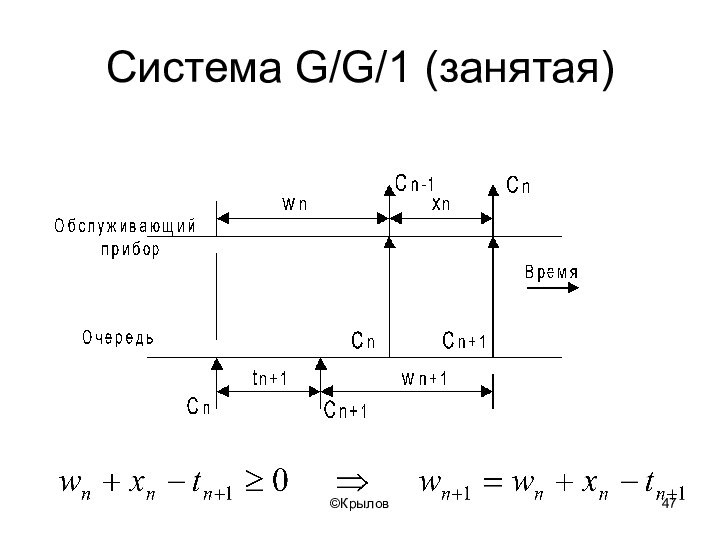
- 47. ©КрыловCистема G/G/1 (занятая)
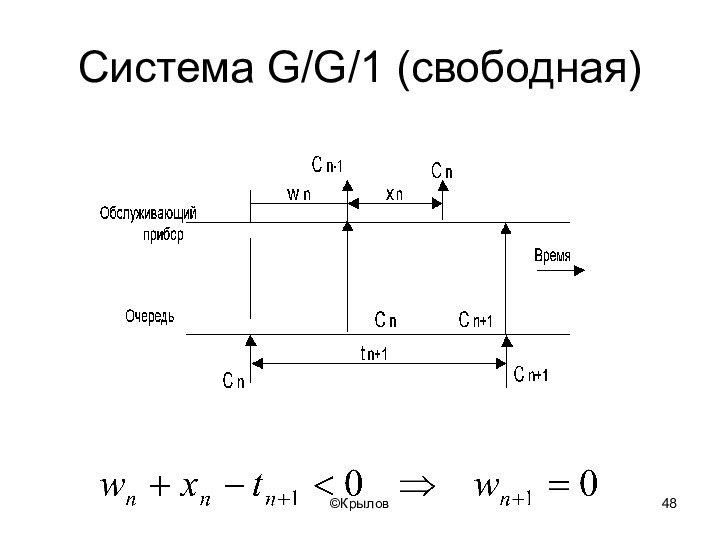
- 48. ©КрыловСистема G/G/1 (свободная)
- 49. ©КрыловСвязанная марковская цепь
- 50. ©КрыловРешение (уравнение Линдли)
- 51. ©КрыловРешение уравнения Линдли
- 52. ©КрыловПриближенное решение
- 53. ©КрыловПриближенное решение
- 54. ©КрыловВерхняя граница,граница Маршалла
- 55. ©КрыловНижняя граница для потоков с монотонностью
- 56. ©КрыловУточненная нижняя граница
- 57. Скачать презентацию
- 58. Похожие презентации
АНАЛИТИЧЕСКИЕ МЕТОДЫ В ТЕОРИИ ТЕЛЕТРАФИКА Андрей Андреевич Марков родился 14 июня 1856. В цикле работ, опубликованном в 1906-1912гг., заложил основы одной из общих схем естественных процессов, которые можно изучать методами математического анализа. Впоследствии эта схема была









![Теория телетрафика ©КрыловНепрерывные цепи МарковаH(t) = [pij(t)] - матрица вероятностей перехода из состояния i](/img/tmb/14/1346566/4bb5a2fbb19ffbe3aeb7c0c3b86bdaa2-720x.jpg)



























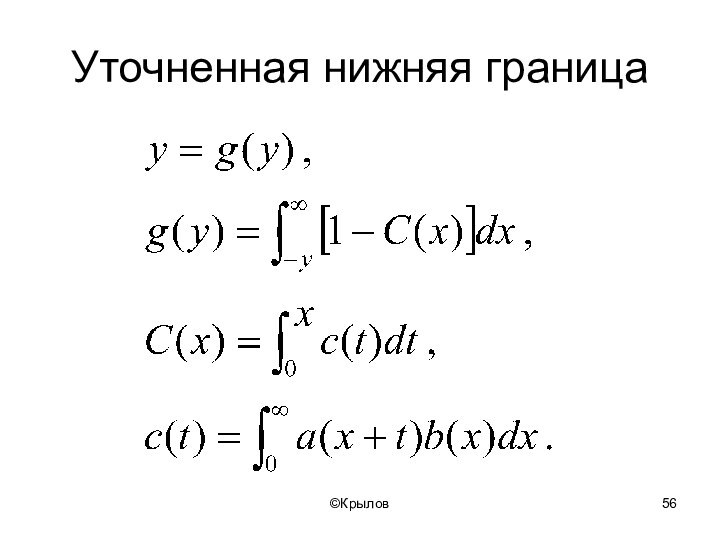
Слайд 3
©Крылов
Вероятностная модель СМО
дискретная цепь Маркова
однородная цепь Маркова
неприводимая
цепь Маркова
Возвратное и невозвратное состояние
Периодическое и апериодическое возвратное
состояниеВозвратное нулевое и возвратное ненулевое
Слайд 4
©Крылов
Цепи Маркова
Теорема 1.
Состояния неприводимой цепи Маркова либо все
невозвратные, либо все возвратные нулевые, либо все возвратные ненулевые.
В случае периодической цепи все состояния имеют один и тот же период
Слайд 5
©Крылов
Цепи маркова
Для неприводимой и апериодической цепи Маркова всегда
существуют предельные вероятности, не зависящие от начального распределения вероятностей
все состояния цепи невозвратные или все возвратные нулевые, и тогда все предельные вероятности равны нулю и стационарного состояния не существует
все состояния возвратные ненулевые и тогда существует стационарное распределение вероятностей
Слайд 6
©Крылов
Цепи Маркова
Состояние называется эргодическим, если оно апериодично и
возвратно ненулевое. Если все состояния цепи Маркова эргодичны, то
вся цепь называется эргодической. Предельные вероятности эргодической цепи Маркова называют вероятностями состояния равновесия, имея в виду, что зависимость от начального распределения вероятностей полностью отсутствует.
Слайд 10
©Крылов
Непрерывные цепи Маркова
Случайный процесс X(t) с
дискретным множеством значений образует непрерывную цепь Маркова, если
Уравнение
Чепмена – Колмогорова
Слайд 11
©Крылов
Непрерывные цепи Маркова
H(t) = [pij(t)] - матрица вероятностей
перехода из состояния i в состояние j в момент
времени t , а матрица Q называется матрицей интенсивностей переходовИнтенсивности вероятностей переходов qij(t)





























