Слайд 2
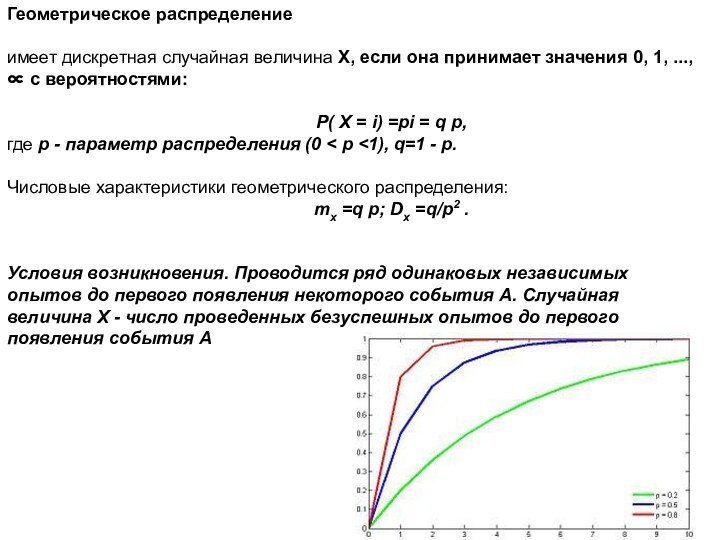
Геометрическое распределение
имеет дискретная случайная величина Х, если она
принимает значения 0, 1, ...,∝ с вероятностями:
Р( X =
i) =pi = q p,
где p - параметр распределения (0 < p <1), q=1 - p.
Числовые характеристики геометрического распределения:
mx =q p; Dx =q/p2 .
Условия возникновения. Проводится ряд одинаковых независимых опытов до первого появления некоторого события А. Случайная величина Х - число проведенных безуспешных опытов до первого появления события А
Слайд 3
Представьте, вы бросаете монету, вероятность успеха, например, выпадения
герба есть p, вероятность неудачи q = 1 – p.
Посчитаем, сколько
раз вам нужно бросить монету до появления первого успеха (первого герба).
Обозначим эту величину через ν .
Очевидно, это случайная величина.
Зададимся вопросом: какое распределение имеет данная случайная величина?
Ответ прост: случайная величина n имеет геометрическое распределение, задаваемое формулой:
где k= 1, 2…
В частности, вероятность того, что герб выпадет на первом шаге равна
Вероятность того, что герб выпадает впервые на втором шаге (а до того выпадала решетка), равна и т.д.
Геометрическое распределение является частным случаем отрицательного биномиального распределения.
Геометрическая случайная величина обладает свойством отсутствия последействия: знание о том, что у вас не было успеха в течение n предыдущих бросков, никак не влияет на распределение оставшегося числа бросков до появления герба.
Слайд 4
Биномиальное распределение
имеет дискретная случайная величина X, если она
принимает значения 0, 1, ..., n со следующими вероятностями
где
n, p - параметры распределения (0 < p < 1), q = 1 - p.
Числовые характеристики биномиального распределения:
mx = np; Dx = nqp.
Условия возникновения. Проводится n одинаковых независимых испытаний, в каждом из которых событие А появляется с вероятностью р. Случайная величина Х - число опытов, в которых произошло событие А.
Слайд 5
Если использовать только бумагу и калькулятор, то расчеты
по формуле биноминального распределения, несмотря на отсутствие интегралов, даются
довольно тяжело.
К примеру значение 100! – имеет более 150 знаков. Вручную рассчитать такое невозможно.
Раньше, да и сейчас тоже, для вычисления подобных величин использовали приближенные формулы.
В настоящий момент целесообразно использовать специальное ПО, типа MS Excel. Таким образом, любой пользователь вполне может вычислить вероятность значения биномиально распределенной случайной величины.
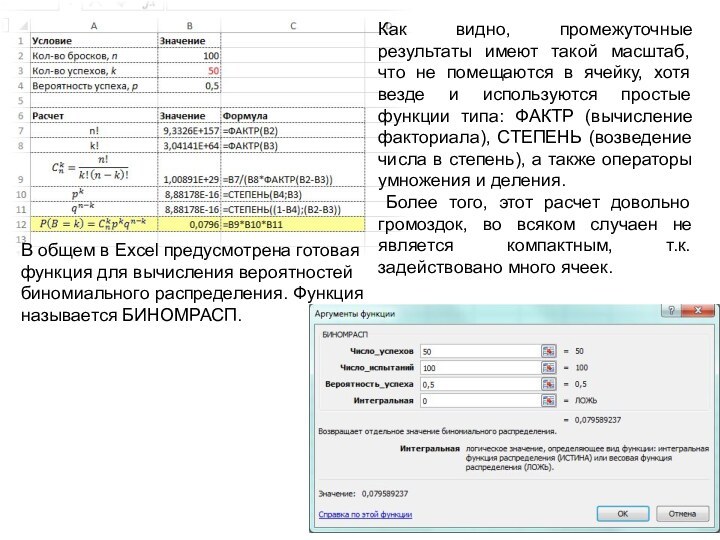
Для закрепления материала задействуем Excel пока в качестве обычного калькулятора, т.е. произведем поэтапное вычисление по формуле биномиального распределения. Рассчитаем, например, вероятность выпадения 50 орлов..
Слайд 6
Как видно, промежуточные результаты имеют такой масштаб, что
не помещаются в ячейку, хотя везде и используются простые
функции типа: ФАКТР (вычисление факториала), СТЕПЕНЬ (возведение числа в степень), а также операторы умножения и деления.
Более того, этот расчет довольно громоздок, во всяком случаен не является компактным, т.к. задействовано много ячеек.
В общем в Excel предусмотрена готовая функция для вычисления вероятностей биномиального распределения. Функция называется БИНОМРАСП.
Слайд 7
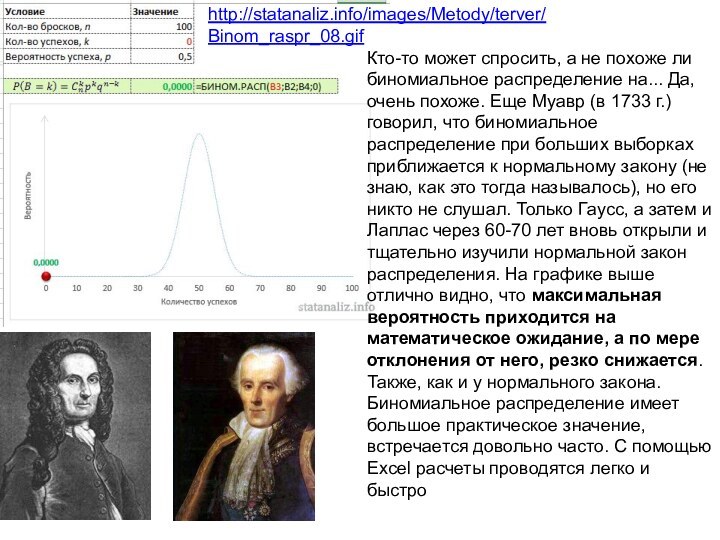
http://statanaliz.info/images/Metody/terver/Binom_raspr_08.gif
Кто-то может спросить, а не похоже ли биномиальное
распределение на... Да, очень похоже. Еще Муавр (в 1733
г.) говорил, что биномиальное распределение при больших выборках приближается к нормальному закону (не знаю, как это тогда называлось), но его никто не слушал. Только Гаусс, а затем и Лаплас через 60-70 лет вновь открыли и тщательно изучили нормальной закон распределения. На графике выше отлично видно, что максимальная вероятность приходится на математическое ожидание, а по мере отклонения от него, резко снижается. Также, как и у нормального закона.
Биномиальное распределение имеет большое практическое значение, встречается довольно часто. С помощью Excel расчеты проводятся легко и быстро
Слайд 8
Распределение Пуассона
имеет дискретная случайная величина Х, если
она принимает
значения 0, 1, …, ∝
со следующими вероятностями:
Условия возникновения:
Распределение Пуассона является предельным случаем биномиального, когда число опытов n неограниченно увеличивается, а вероятность p события A в одном опыте стремится к 0, так что существует предел
Случайная величина Х - число событий пуассоновского потока, поступивших в течение интервала τ, причем параметр а = λτ,
где λ - интенсивность потока.
Слайд 9
Рассмотрим временную ось, на которой будем отмечать моменты
возникновения случайных событий (например, отказы компонентов в сложном техническом
устройстве, заявки на обслуживание и т.п.).
Последовательность таких моментов называется потоком случайных событий.
Поток случайных событий называется стационарным, если число событий, приходящихся на интервал г, в общем случае не зависит от расположения этого участка на временной оси и определяется только его длительностью, т.е. среднее число событий в единице времени λ (интенсивность потока) постоянно.
Слайд 10
Поток случайных событий называется ординарным, если
вероятность попадания
в некоторый участок
Δt двух и более случайных событий
значительно меньше, чем вероятность попадания 1-го события.
В потоке отсутствует последействие, если вероятность попадания событий на участок τ не зависит от того, сколько событий попало на другие участки, не пересекающиеся с данным.
Поток случайных событий называется пуассоновским или простейшим, если он является стационарным, ординарным и без последействия.
Слайд 11
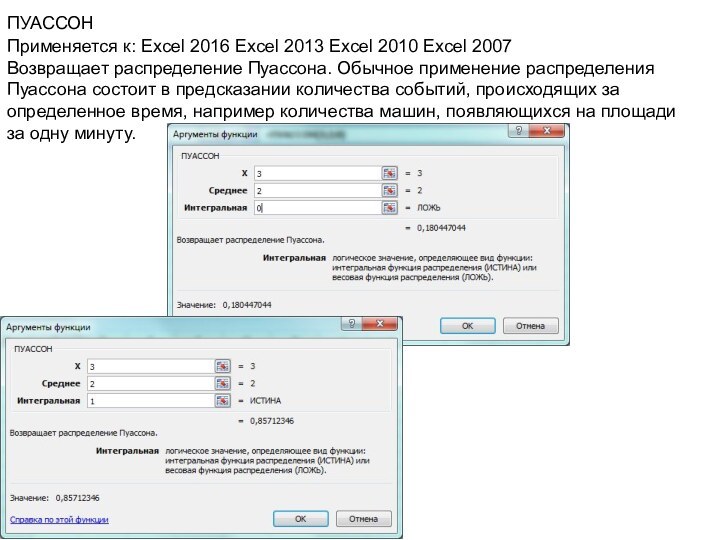
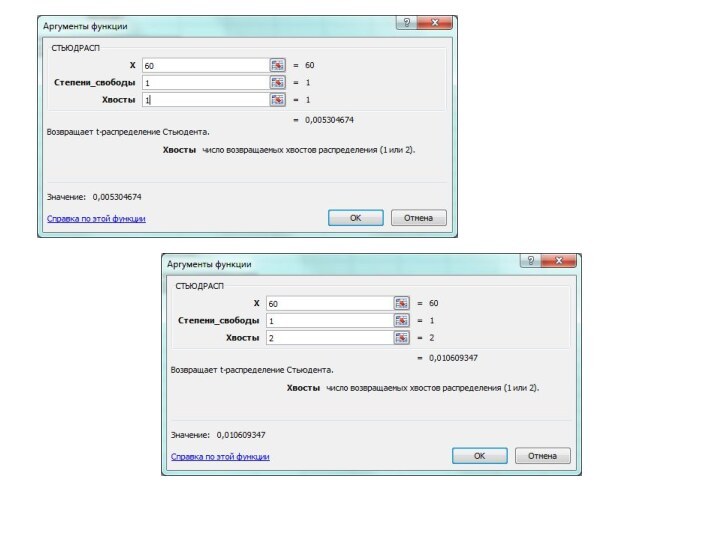
Применяется к: Excel 2016 Excel 2013 Excel 2010 Excel 2007
Возвращает распределение Пуассона. Обычное
применение распределения Пуассона состоит в предсказании количества событий, происходящих
за определенное время, например количества машин, появляющихся на площади за одну минуту.
ПУАССОН
Слайд 12
x Обязательный. Количество событий.
Среднее Обязательный. Ожидаемое числовое значение.
Интегральная
Обязательный.
Логическое значение, определяющее форму возвращаемого распределения вероятностей. Если
аргумент "интегральная" имеет значение ИСТИНА, то функция ПУАССОН возвращает интегральное распределение Пуассона, то есть вероятность того, что число случайных событий окажется в диапазоне от 0 до x включительно. Если этот аргумент имеет значение ЛОЖЬ, то возвращается весовая функция распределения Пуассона, то есть вероятность точного равенства числа произошедших событий значению x.
Слайд 13
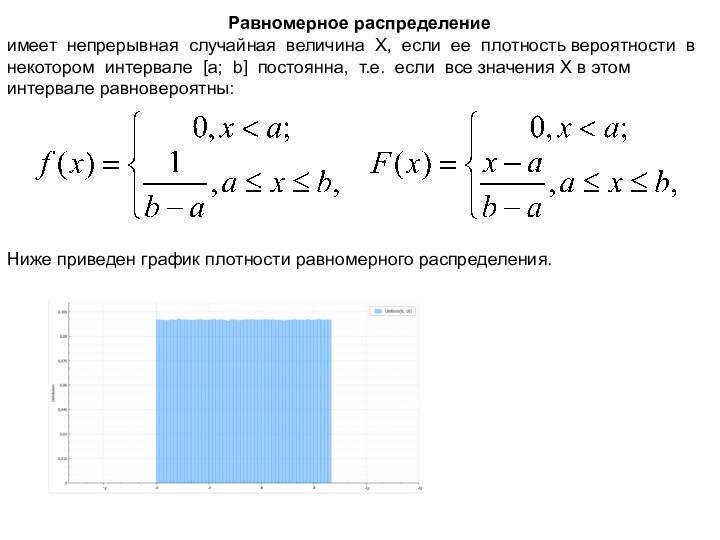
Равномерное распределение
имеет непрерывная случайная величина Х, если
ее плотность вероятности в некотором интервале [а; b] постоянна,
т.е. если все значения X в этом интервале равновероятны:
Ниже приведен график плотности равномерного распределения.
Слайд 14
Числовые характеристики равномерно распределенной случайной величины:
При необходимости определения
параметров a и b по известным mx, Dx используют
следующие формулы:
Условия возникновения:
Случайная величина Х - ошибки округления при ограниченной разрядной сетке:
округление до меньшего целого, X □ [-1; 0], mx = - 0,5;
округление до большего целого, X □ [-0; 1], mx = 0,5;
округление до ближайшего целого, X □ [- 0,5; 0,5], mx = 0, где 1 - вес младшего разряда.
Случайная величина Х - погрешность считывания значений с аналоговой шкалы измерительного прибора, X □ [- 0,5; 0,5], mx = 0, где 1- цена деления шкалы.
Генераторы псевдослучайных величин, например RANDOM, встроенные в языки программирования высокого уровня.
Слайд 15
Преобразование равномерно распределенной случайной величины в нормально распределенную
Этот
вопрос уже давно подробно изучен, и наиболее широкое распространение
получил метод полярных координат, предложенный Джорджем Боксом, Мервином Мюллером и Джорджем Марсальей в 1958 году.
Данный метод позволяет получить пару независимых нормально распределенных случайных величин с математическим ожиданием 0 и дисперсией 1 следующим образом:
где Z0 и Z1 — искомые значения, s = u2 + v2, а u и v — равномерно распределенные на отрезке (-1, 1) случайные величины, подобранные таким образом, чтобы выполнялось условие
0 < s < 1.
Слайд 16
Экспоненциальное распределение
или показательное распределение имеет непрерывная
случайная
величина T, принимающая только положительные
значения, если ее плотность
вероятности и функция распределения
равны:
где λ - параметр распределения (λ > 0).
Ниже приведены графики плотности и функции экспоненциального распределения.
Слайд 17
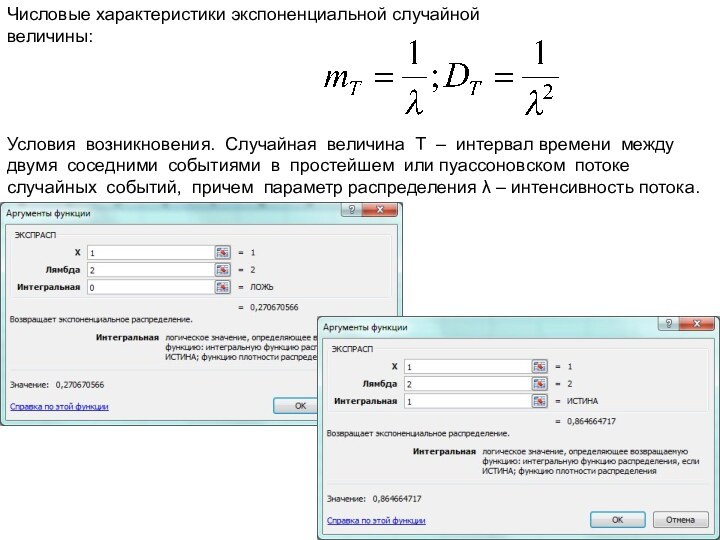
Числовые характеристики экспоненциальной случайной
величины:
Условия
возникновения. Случайная величина T – интервал времени между двумя
соседними событиями в простейшем или пуассоновском потоке случайных событий, причем параметр распределения λ – интенсивность потока.
Слайд 18
Распределение χ (хи - квадрат)
Рассмотрим распределение некоторых случайных
величин, представляющих функции нормальных величин, используемых в математической статистике.
Пусть
случайная величина Y, распределена по нормальному закону .
Тогда случайная величина
распределена по нормальному закону с параметрами
Квадрат такой стандартизованной случайной величины
называется случайной величиной χ2 (хи - квадрат) с одной степенью свободы.
Слайд 19
Рассмотрим n независимых случайных величин Y1, Y2, ...,
Yn, распределенных по нормальному закону с M(Yi) = ai
и средними квадратическими отклонениями σi, i=1…n.
Образуем для каждой из этих случайных величин стандартизованную случайную величину
Сумма квадратов стандартизованных переменных
Слайд 20
называется случайной величиной χ2 с n степенями свободы.
Плотность распределения случайной величины х имеет вид:
где
гамма-функция Эйлера
и является обобщением понятия факториала: Г(р)=(р-1)! для целых положительных p.
Слайд 21
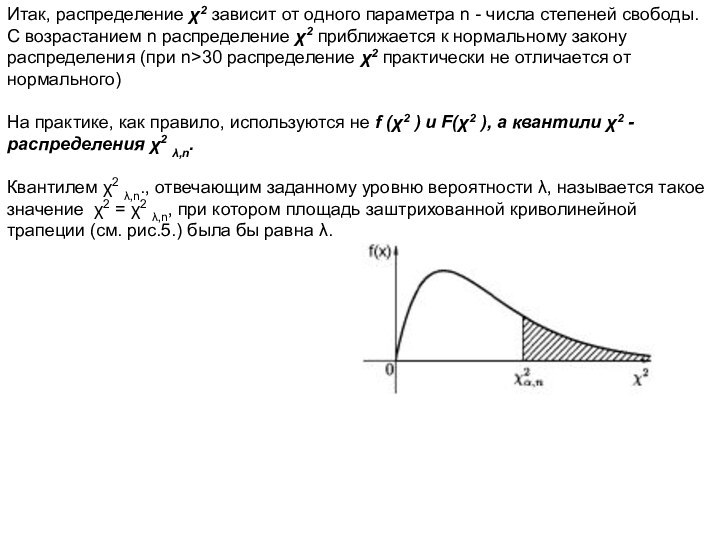
Итак, распределение χ2 зависит от одного параметра n
- числа степеней свободы. С возрастанием n распределение χ2
приближается к нормальному закону распределения (при n>30 распределение χ2 практически не отличается от нормального)
На практике, как правило, используются не f (χ2 ) и F(χ2 ), а квантили χ2 - распределения χ2 λ,n.
Квантилем χ2 λ,n., отвечающим заданному уровню вероятности λ, называется такое значение χ2 = χ2 λ,n, при котором площадь заштрихованной криволинейной трапеции (см. рис.5.) была бы равна λ.
Слайд 22
Распределение Стьюдента
Распределение Стьюдента (t–распределение) имеет важное значение
при статистических вычислениях, связанных с нормальным законом, а именно
тогда, когда среднее квадратическое отклонение σ неизвестно и подлежит определению по опытным данным.
Пусть Y: Y1, Y2, ..., Yn – независимые случайные величины, имеющие нормальное распределение с параметрами M (Y)=M (Yi)=0 и
σY = σYi =1, i =1,n .
Случайная величина
является функцией нормально распределенных случайных величин и называется безразмерной дробью Стьюдента.
Слайд 23
Плотность распределения случайной величины t имеет вид:
где n
- число слагаемых в подкоренном выражении дроби Стьюдента.
Из формулы
видно, что распределение случайной величины t зависит только от одного параметра - числа степеней свободы n, равного числу слагаемых в подкоренном выражении дроби Стьюдента ( ).
Известно, что математическое ожидание и дисперсия случайной
величины t соответственно равны
Слайд 24
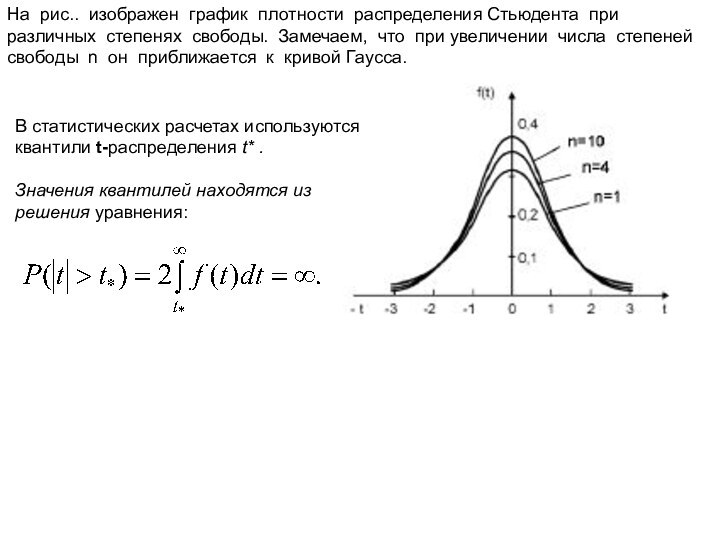
На рис.. изображен график плотности распределения Стьюдента при
различных степенях свободы. Замечаем, что при увеличении числа степеней
свободы n он приближается к кривой Гаусса.
В статистических расчетах используются квантили t-распределения t* .
Значения квантилей находятся из решения уравнения:
Слайд 25
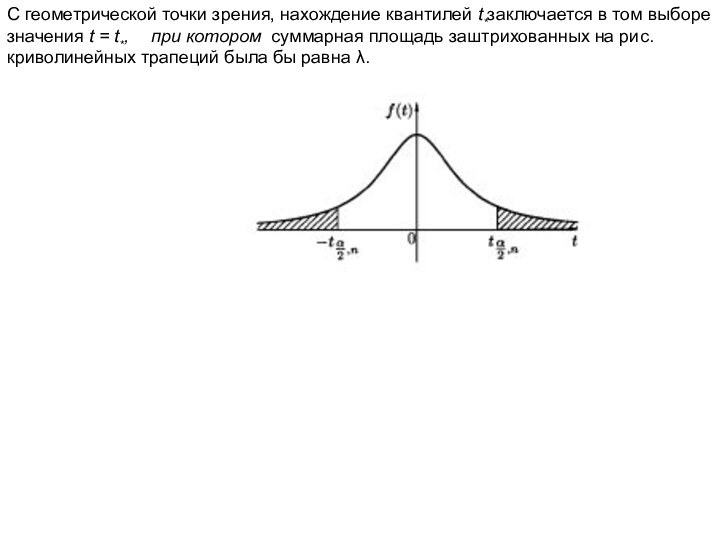
С геометрической точки зрения, нахождение квантилей t*заключается в
том выборе значения t = t*, при котором суммарная площадь
заштрихованных на рис. криволинейных трапеций была бы равна λ.
Слайд 26
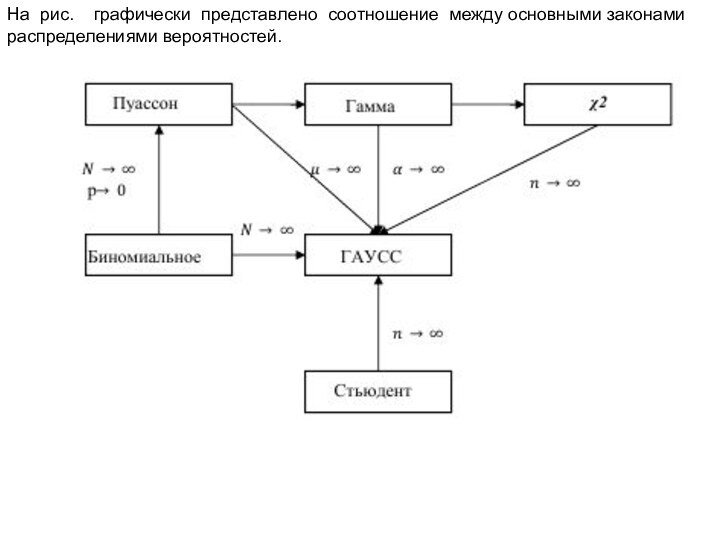
На рис. графически представлено соотношение между основными
законами распределениями вероятностей.