Слайд 2
Прямые и плоскость
Прямая является идеализацией тонкой натянутой нити,
края стола прямоугольной формы. По прямой распространяется луч света.
Прямые
проводятся на листе бумаги или доске с помощью линейки. Хотя изображения прямых ограничены, их следует представлять себе неограниченно продолженными в обе стороны.
Плоскость является идеализацией ровной поверхности воды, поверхности стола, доски, зеркала и т.п.
Слайд 3
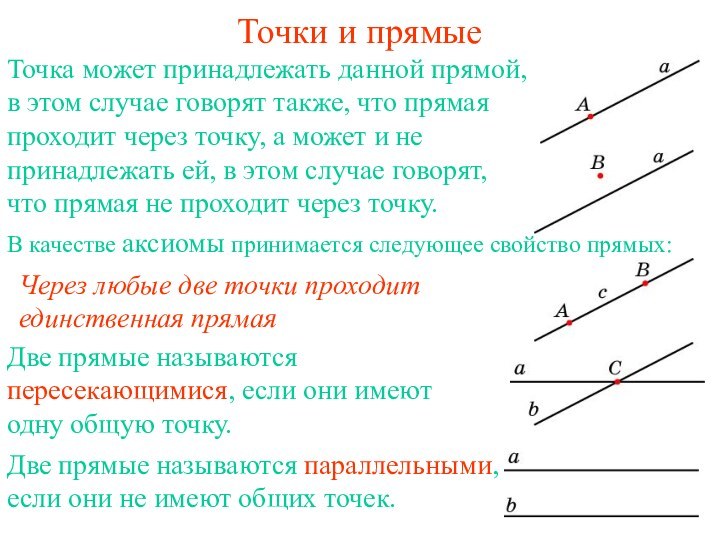
Точки и прямые
В качестве аксиомы принимается следующее свойство
прямых:
Слайд 4
Обозначения
Точка A, точка B, точка C, …
A, B,
C, …
a, b, c, …
AB, CD, …
Прямая a, прямая
b, …
Прямая AB, прямая CD, …
Точка A принадлежит прямой a.
Точка B не принадлежит прямой a.
Слайд 5
Вопрос 1
Какие геометрические фигуры являются основными?
Ответ: Точка,
прямая, плоскость.
Слайд 6
Вопрос 2
Какие объекты идеализирует точка?
Ответ: Точка является
идеализацией очень маленьких объектов, т.е. таких, размерами которых можно
пренебречь.
Слайд 7
Вопрос 3
Какие объекты идеализирует прямая?
Ответ: Прямая является
идеализацией тонкой натянутой нити, края стола прямоугольной формы, по
прямой распространяется свет.
Слайд 8
Вопрос 4
Какие объекты идеализирует плоскость?
Ответ: Плоскость является
идеализацией ровной поверхности воды, поверхности стола, доски, зеркала и
т.п.
Слайд 9
Вопрос 5
Как Евклид определял точку?
Ответ: Евклид определял точку
как то, что не имеет частей.
Слайд 10
Вопрос 6
Как изображаются точки?
Ответ: Точки изображаются остро отточенным
карандашом или ручкой на листе бумаги, мелом на доске
и т.п.
Слайд 11
Вопрос 7
Как обозначаются точки?
Ответ: Точки обозначаются прописными
латинскими буквами A, B, C, ….
Слайд 12
Вопрос 8
Как проводятся прямые?
Ответ: Прямые проводятся на
листе бумаги или доске с помощью линейки.
Слайд 13
Вопрос 9
Как обозначаются прямые?
Ответ: Прямые обозначаются строчными
латинскими буквами a, b, c, ..., или двумя прописными
латинскими буквами AB, CD, ... .
Слайд 14
Вопрос 10
Какие свойства основных геометрических фигур называются аксиомами?
Ответ: Аксиомами называются свойства геометрических фигур, принимаемые без доказательства.
Слайд 15
Вопрос 11
Как переводится слово «аксиома» с греческого языка?
Ответ:
Достойное признания, не вызывающее сомнения
Слайд 16
Вопрос 12
Как могут располагаться друг относительно друга точка
и прямая?
Ответ: Точка может принадлежать данной прямой, а может
и не принадлежать ей.
Слайд 17
Вопрос 13
Какое свойство принимается в качестве аксиомы взаимного
расположения точек и прямой?
Ответ: Через любые две точки проходит
единственная прямая.
Слайд 18
Вопрос 14
Какие две прямые называются пересекающимися?
Ответ: Две прямые
называются пересекающимися, если они имеют одну общую точку.
Слайд 19
Вопрос 15
Какие две прямые называются параллельными?
Ответ: Две прямые
называются параллельными, если они не имеют ни одной общей
точки.
Слайд 20
Упражнение 1
Сколько прямых можно провести через: а) одну
точку; б) две точки?
Ответ: а) Бесконечно много; б) одну.
Слайд 21
Упражнение 2
Сколько прямых можно провести через три точки?
Ответ: Либо одну, либо ни одной.
Слайд 22
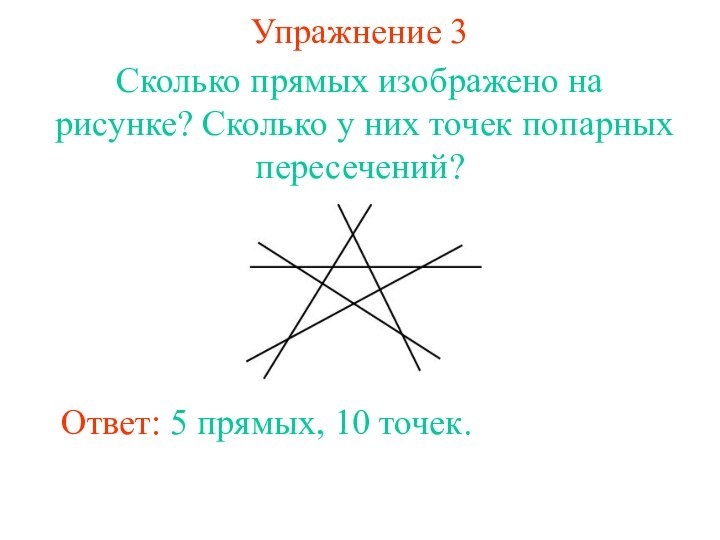
Упражнение 3
Сколько прямых изображено на рисунке? Сколько у
них точек попарных пересечений?
Ответ: 5 прямых, 10 точек.
Слайд 23
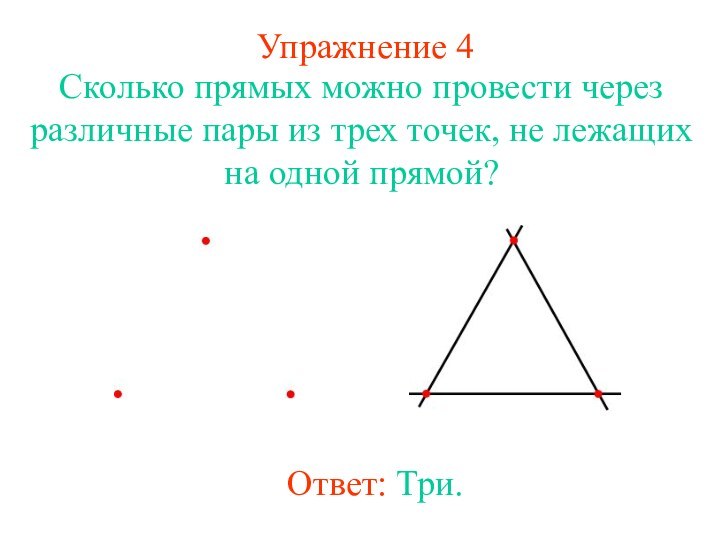
Упражнение 4
Сколько прямых можно провести через различные пары
из трех точек, не лежащих на одной прямой?
Ответ:
Три.
Слайд 24
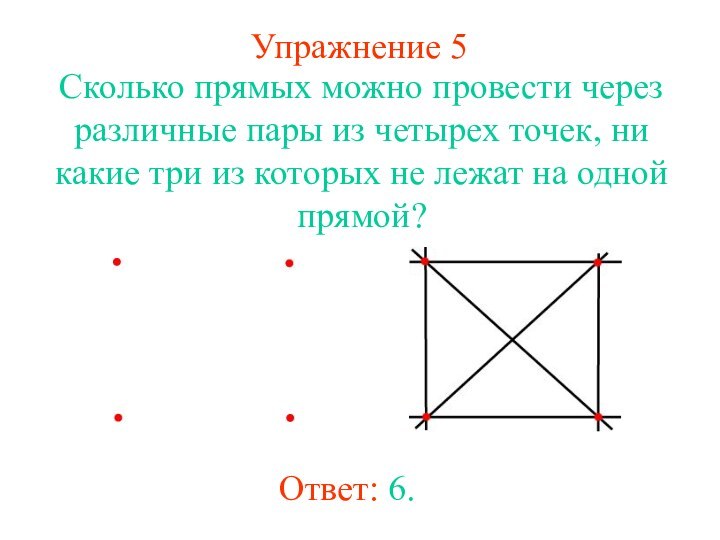
Упражнение 5
Сколько прямых можно провести через различные пары
из четырех точек, ни какие три из которых не
лежат на одной прямой?
Ответ: 6.
Слайд 25
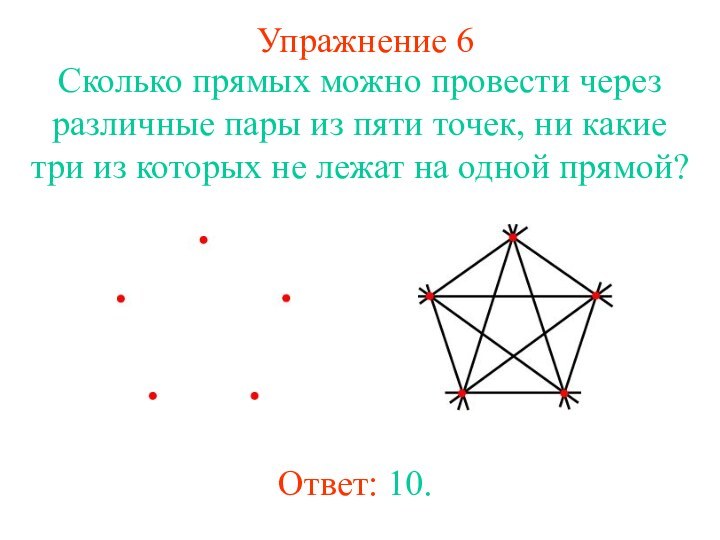
Упражнение 6
Сколько прямых можно провести через различные пары
из пяти точек, ни какие три из которых не
лежат на одной прямой?
Ответ: 10.
Слайд 26
Упражнение 7
Сколько прямых можно провести через различные пары
из n точек, ни какие три из которых не
лежат на одной прямой?
Слайд 27
Упражнение 8
Сколько различных точек попарных пересечений могут иметь
три прямые?
Ответ: Ни одной, одну, две, три.
Слайд 28
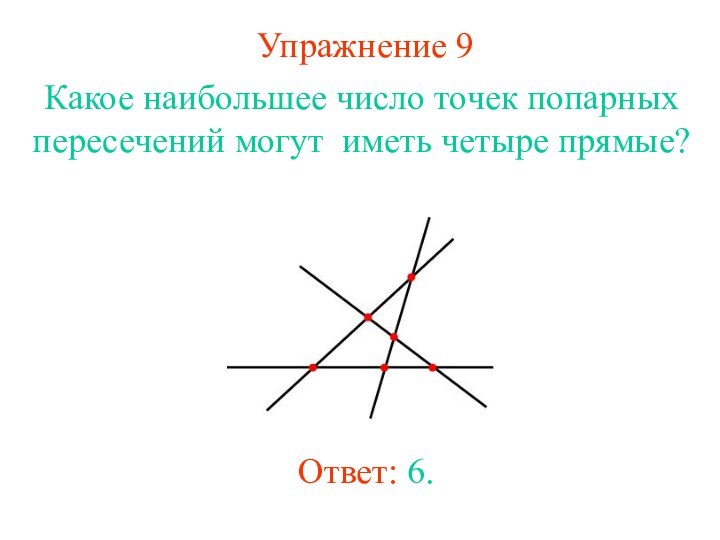
Упражнение 9
Какое наибольшее число точек попарных пересечений могут
иметь четыре прямые?
Ответ: 6.
Слайд 29
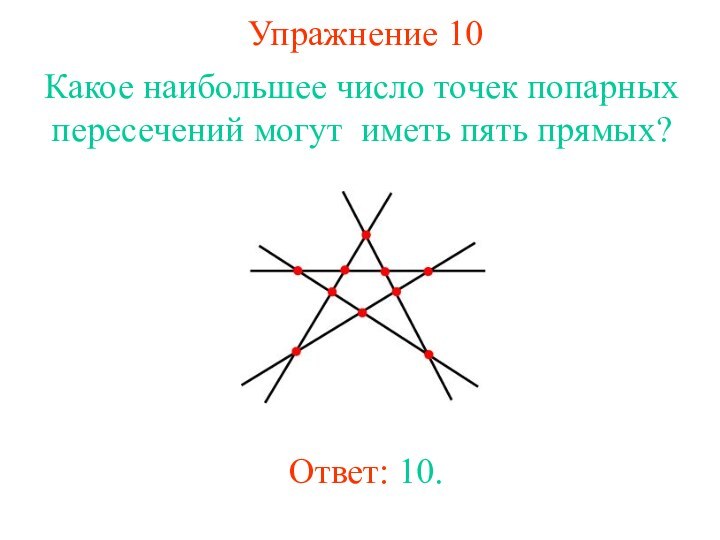
Упражнение 10
Какое наибольшее число точек попарных пересечений могут
иметь пять прямых?
Ответ: 10.