Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

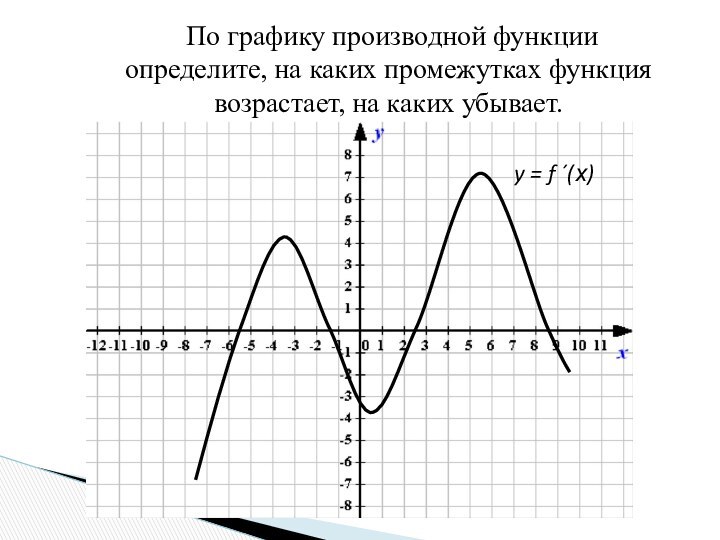
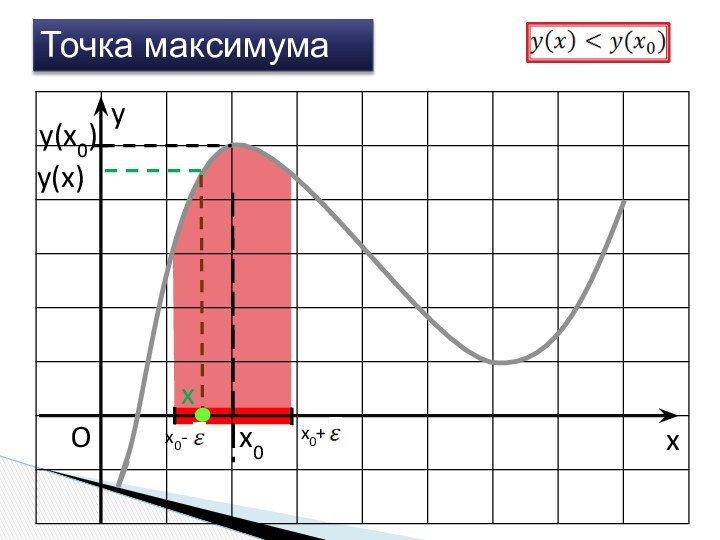
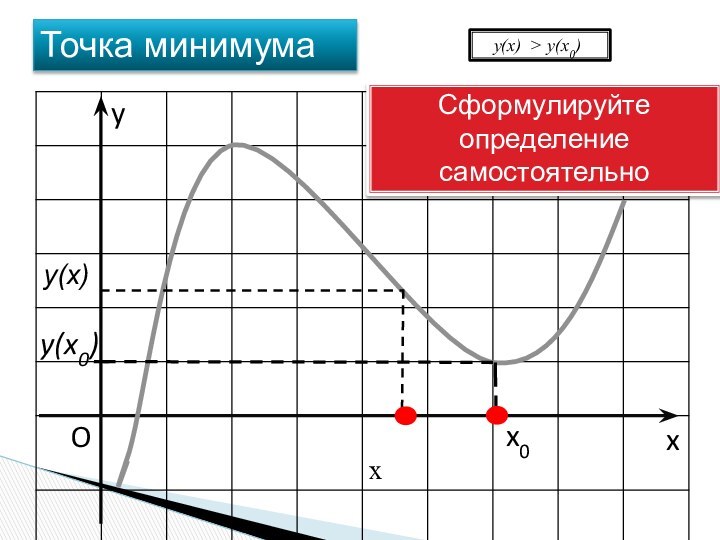
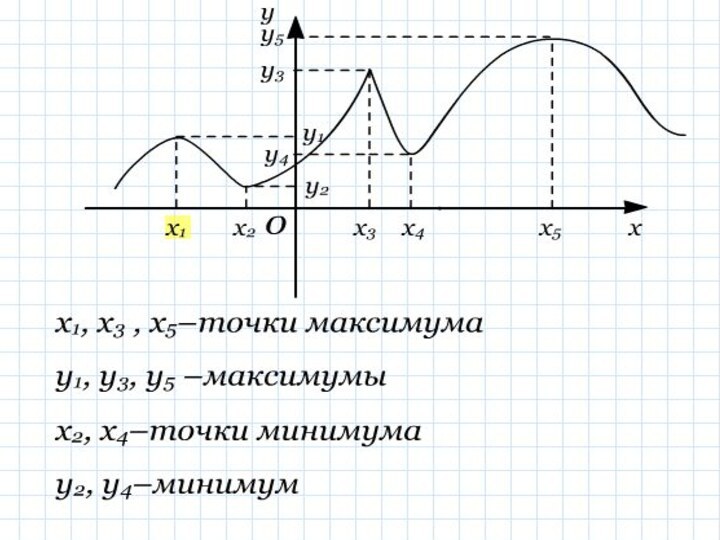
Презентация на тему Точки максимума и минимума

Содержание

 Найти область определения и производную функции:
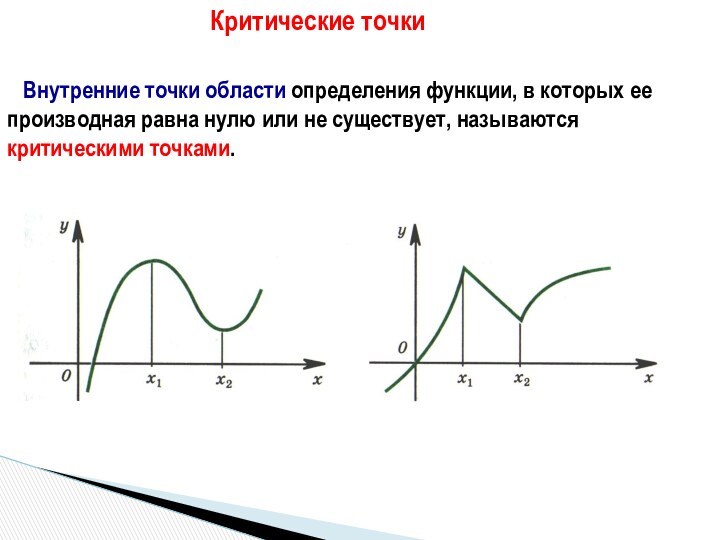
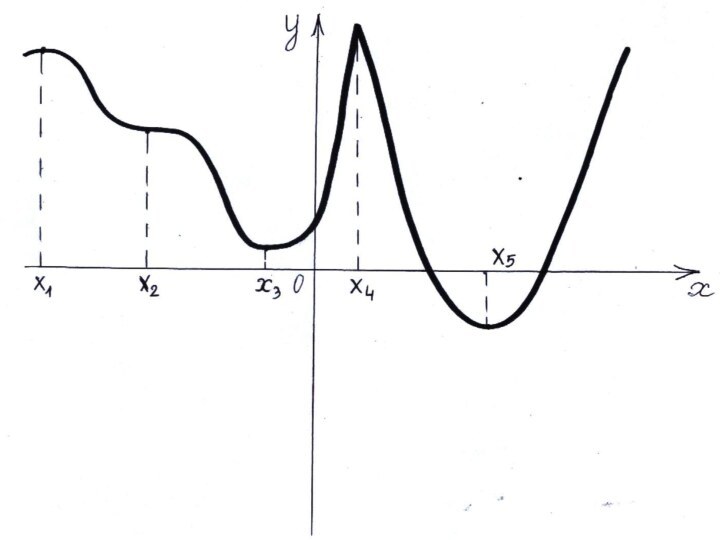
Урок алгебры в 11 классе по теме: «Точки максимума и минимума»  Найти область определения и производную функции:  Найти значения х, при которых значение f(x) равно 0 -5х + 1 > 0; х2 + 2х - 3 xyO11479121519По графику функции определите, на каких промежутках производная функции положительна, на каких - отрицательна? По графику производной функции определите, на каких промежутках функция возрастает, на xyOx0Точка максимумаx0+x0-xy(x0)y(x) xOx0Точка минимумаy(x0)yСформулируйте определение самостоятельноy(х) > y(x0) Точки максимума и минимума называются точками экстремума функции Теорема Ферма.  Внутренние точки области определения функции, в которых ее производная равна Для того, чтобы точка была точкой экстремума функции необходимо, чтобы эта точка Для того , чтобы точка х0 была точкой экстремума функции f(х):необходимо , Найти производную функции.Решить уравнение f ´(х)=0, и найти тем самым стационарные точки.Методом xyO11479121519Найти по графику функции точки, с определениями которых вы только, что познакомились. Решение:1) Найдем производную функции:f ´ (x)=92) Найдем стационарные точки:Стационарных точек нет.3) Данная XЄ Ry'=2x-2Точек, в которых производная не существует нет;y‘=0 при х=1 № 5.6 (а) решение у доски № 5.7 (в)решение у доски с ДОМАШНЕЕ ЗАДАНИЕ1. п. 5.1, выучить определения и алгоритм нахождения точек экстремума., №5.8
Слайды презентации

Слайд 2  
Найти область определения и производную функции:

 Найти область определения и производную функции:

Слайд 3  
Найти значения х, при которых значение f(x) равно

 Найти значения х, при которых значение f(x) равно 0

Слайд 4 -5х + 1 > 0;

х2

-5х + 1 > 0; х2 + 2х - 3

+ 2х - 3 < 0;

(х

+ 2)ех < 0.

Решить неравенство

Слайд 5 x
y
O
1
1
4
7
9
12
15
19
По графику функции определите, на каких промежутках производная

xyO11479121519По графику функции определите, на каких промежутках производная функции положительна, на каких - отрицательна?

функции положительна, на каких - отрицательна?

Слайд 6 По графику производной функции определите, на каких

По графику производной функции определите, на каких промежутках функция возрастает,

промежутках функция возрастает, на каких убывает.
y = f ´(х)

Слайд 7 x
y
O
x0
Точка максимума
x0+
x0-
x
y(x0)
y(x)

xyOx0Точка максимумаx0+x0-xy(x0)y(x)

Слайд 8 x
O
x0
Точка минимума
y(x0)
y
Сформулируйте определение самостоятельно
y(х) > y(x0)

xOx0Точка минимумаy(x0)yСформулируйте определение самостоятельноy(х) > y(x0)

Слайд 9 Точки максимума и минимума называются
точками экстремума функции

Точки максимума и минимума называются точками экстремума функции

Слайд 10

Слайд 11 Теорема Ферма.
 

Теорема Ферма. 

Слайд 12 Внутренние точки области определения функции, в

Внутренние точки области определения функции, в которых ее производная равна

которых ее производная равна нулю или не существует, называются

критическими точками.

Критические точки

Слайд 13 Для того, чтобы точка была точкой экстремума функции

Для того, чтобы точка была точкой экстремума функции необходимо, чтобы эта

необходимо, чтобы эта точка была критической точкой данной функции
Но

это условие не является достаточным

Слайд 14

Слайд 15

Слайд 16

Слайд 17 Для того , чтобы точка х0 была точкой

Для того , чтобы точка х0 была точкой экстремума функции f(х):необходимо

экстремума функции f(х):
необходимо , чтобы х0 была критической точкой

функции;
достаточно, чтобы при переходе через критическую точку х0 производная меняла знак.

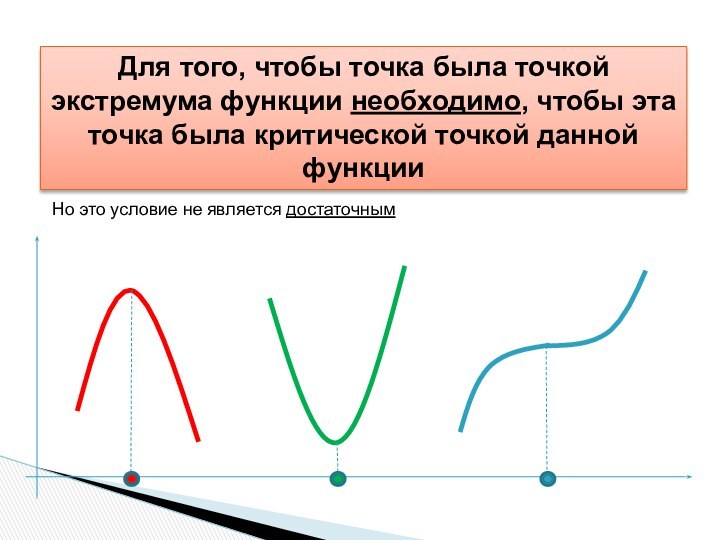
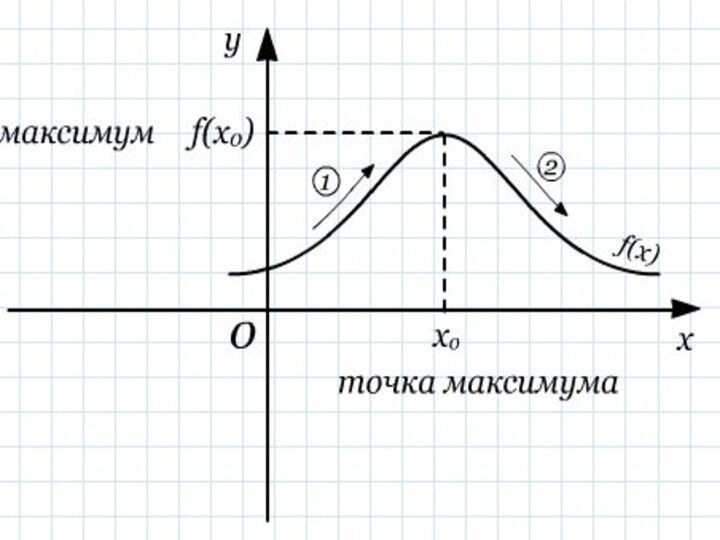
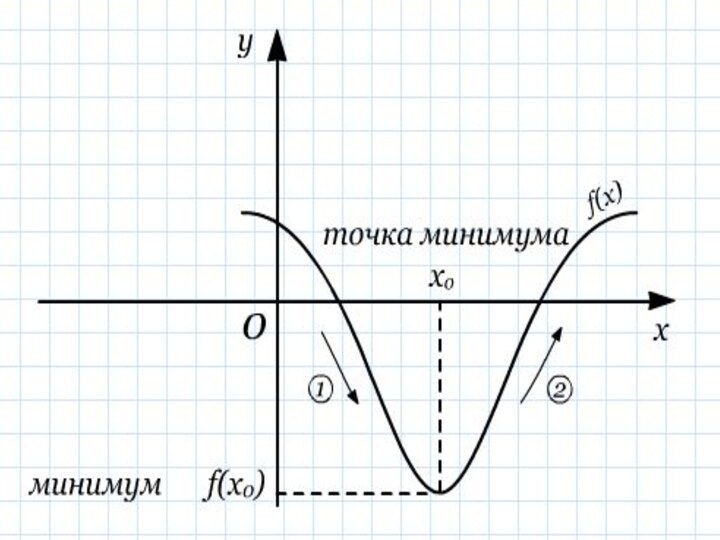
Необходимое и достаточное условие экстремума.

Слайд 18 Найти производную функции.
Решить уравнение f ´(х)=0, и найти

Найти производную функции.Решить уравнение f ´(х)=0, и найти тем самым стационарные

тем самым стационарные точки.
Методом интервалов установить промежутки знакопостоянства производной.
Если

при переходе через точку х0:
- производная не меняет знак, то х0 – точка перегиба;
- производная меняет знак с «+» на «-», то х0 точка максимума;
- производная меняет знак с «-» на «+», то х0 точка минимума.

Алгоритм нахождения точек экстремума:

Слайд 19 x
y
O
1
1
4
7
9
12
15
19
Найти по графику функции точки, с определениями которых

xyO11479121519Найти по графику функции точки, с определениями которых вы только, что познакомились.

вы только, что познакомились.

Слайд 20

Слайд 21 Решение:

1) Найдем производную функции:
f ´ (x)=9
2) Найдем стационарные

Решение:1) Найдем производную функции:f ´ (x)=92) Найдем стационарные точки:Стационарных точек нет.3)

точки:
Стационарных точек нет.
3) Данная функция линейная и возрастает на

всей числовой оси, поэтому точек экстремума функция не имеет.
Ответ: функция f(x)=9х-3 не имеет точек экстремума.

Рассмотрим задание 1: Найти точки экстремума функции f(x)=9х-3.

Слайд 22 XЄ R
y'=2x-2
Точек, в которых производная не существует нет;
y‘=0

XЄ Ry'=2x-2Точек, в которых производная не существует нет;y‘=0 при х=1

при х=1
у '

+ 1 -

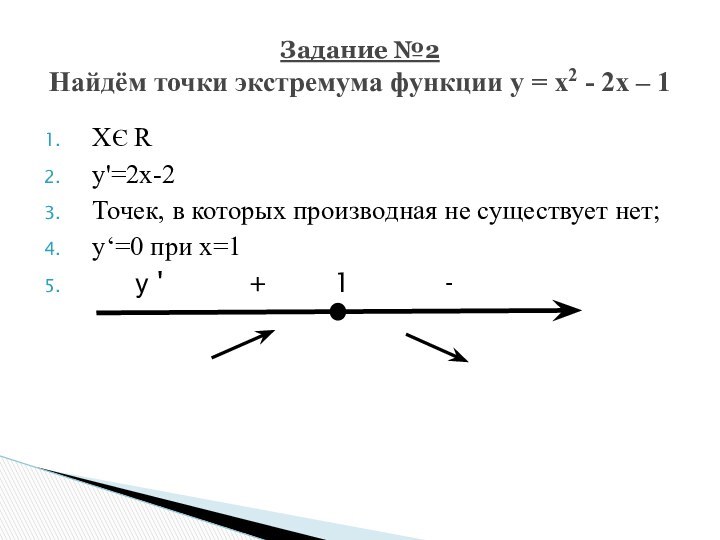
Задание №2 Найдём точки экстремума функции у = х2 - 2х – 1

Слайд 23 № 5.6 (а) решение у доски
№ 5.7

№ 5.6 (а) решение у доски № 5.7 (в)решение у доски

(в)решение у доски с комментарием
№5.10 (а) самостоятельно
Решение задач

  • Имя файла: tochki-maksimuma-i-minimuma.pptx
  • Количество просмотров: 128
  • Количество скачиваний: 0
- Предыдущая Какая цифра в разряде единиц стоит в записи числа 134265?
Следующая - Наибольшее и наименьшее значения функции на отрезке

Похожие презентации

Презентация Игра Найди предмет похожий на квадрат презентация урока для интерактивной доски по математике (старшая группа) Презентация Игра Найди предмет похожий на квадрат презентация урока для интерактивной доски по математике (старшая группа) 111
Интерактивный тренажёр по теме Выполни умножение и деление на 6, на 7 и на 8 Интерактивный тренажёр по теме Выполни умножение и деление на 6, на 7 и на 8 112
Нахождение числа по его дроби Нахождение числа по его дроби 98
Презентация по математике 5 класс . Презентация по математике 5 класс . 114
Теория принятия решений Теория принятия решений 129
Презентация Занимательная геометрия презентация урока для интерактивной доски по математике (подготовительная группа) Презентация Занимательная геометрия презентация урока для интерактивной доски по математике (подготовительная группа) 119
Умножение и деление многозначных чисел Умножение и деление многозначных чисел 128
Определение подобных треугольников. (Упражнение 9. 8 класс) Определение подобных треугольников. (Упражнение 9. 8 класс) 107
Презентация к ООД по ФЭМП в старшей группе презентация к уроку по математике (старшая группа) Презентация к ООД по ФЭМП в старшей группе презентация к уроку по математике (старшая группа) 121
Презентация Запись и название трёхзначных чисел с нулём в разряде единиц презентация к уроку по математике (2 класс) по теме Презентация Запись и название трёхзначных чисел с нулём в разряде единиц презентация к уроку по математике (2 класс) по теме 116
Система работы над развитием пространственных представлений у детей дошкольного возраста через дидактические игры презентация к уроку по математике (старшая группа) Система работы над развитием пространственных представлений у детей дошкольного возраста через дидактические игры презентация к уроку по математике (старшая группа) 45
Задачи на движение по замкнутой линии Задачи на движение по замкнутой линии 119
Двойные неравенства Двойные неравенства 262
Золотое сечение в городе Елец Золотое сечение в городе Елец 112
Конспект урока математики с использованием здоровьесберегающих технологий по теме: Сложение и вычитание трёхзначных чисел 3 класс. план-конспект урока по математике (3 класс) Конспект урока математики с использованием здоровьесберегающих технологий по теме: Сложение и вычитание трёхзначных чисел 3 класс. план-конспект урока по математике (3 класс) 104
Свойства обратных тригонометрических функций Свойства обратных тригонометрических функций 101
Системы счисления. Основные определения, виды, свойства Системы счисления. Основные определения, виды, свойства 92
Признаки параллелограмма Признаки параллелограмма 116
Математические задумки-3 Математические задумки-3 100
Конец 7 Конец 7 105
Презентация по математике на тему Сложение чисел на координатной прямой Презентация по математике на тему Сложение чисел на координатной прямой 90
Решение уравнений 6 класс Решение уравнений 6 класс 96
Конспект занятия по ФЭМП в средней группе с применением ЦОР Путешествие к Лунтику презентация к занятию по математике (средняя группа) по теме Конспект занятия по ФЭМП в средней группе с применением ЦОР Путешествие к Лунтику презентация к занятию по математике (средняя группа) по теме 53
Презентация Закрепление изученного презентация к уроку по математике (2 класс) по теме Презентация Закрепление изученного презентация к уроку по математике (2 класс) по теме 116
Роль математики в профессиях Роль математики в профессиях 149
Луч и угол Луч и угол 163
Натуральные числа Натуральные числа 105
otkrytyy urok matematika chast 1 otkrytyy urok matematika chast 1 242
Интерактивный тренажёр Вычитание чисел вида 37-30 Интерактивный тренажёр Вычитание чисел вида 37-30 95
Методы решения уравнений с одной переменной Методы решения уравнений с одной переменной 137