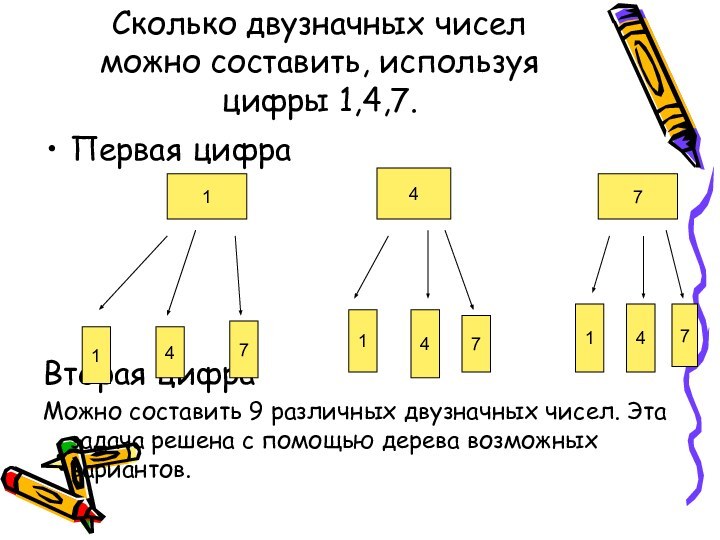
которых нужно подсчитать число всех возможных способов расположения некоторых
предметов или число всех возможных способов осуществления некоторого действия. Разные пути или варианты, которые приходится выбирать человеку, складываются в самые разнообразные комбинации.Введение