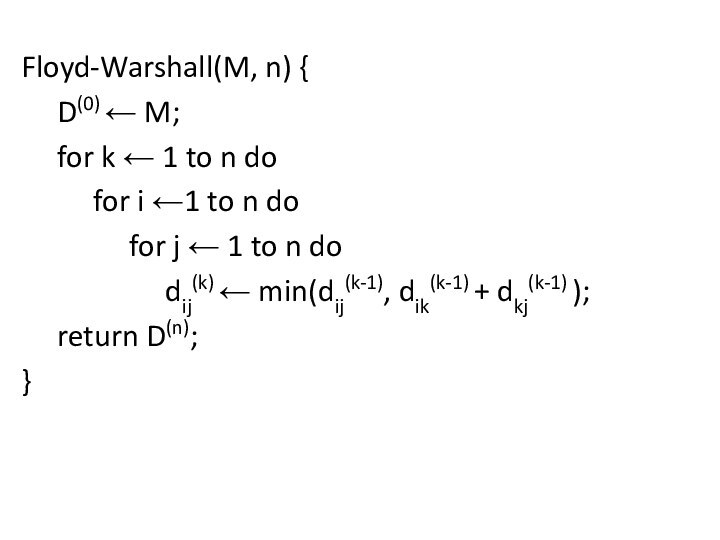Слайд 2
Топологическая сортировка
Определение. Частичным порядком на множестве А называется
отношение R, определенное на А и такое, что
R транзитивно,
для
всех a ∈ A утверждение aRa ложно, т.е. отношение R иррефлексивно.
Из свойств (1) и (2) следует, что если aRb истинно, то bRa ложно (асимметричность).
Слайд 3
Примеры частичного порядка:
решение большой задачи разбивается на ряд
подзадач, над которыми установлен частичный порядок: без решения одной
задачи нельзя решить несколько других;
последовательность чтения курсов в учебных программах: один курс основывается на другом;
выполнение работ: одну работу следует выполнить раньше другой.
Слайд 4
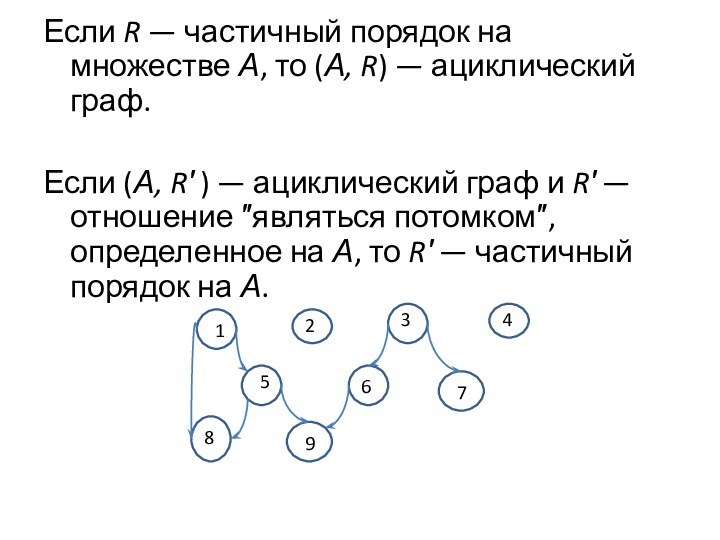
Если R — частичный порядок на множестве А,
то (А, R) — ациклический граф.
Если (А, R′
) — ациклический граф и R′ — отношение ″являться потомком″, определенное на А, то R′ — частичный порядок на А.
1
2
3
4
5
6
7
8
9
Слайд 5
Определение. Линейный порядок R на множестве А —
это такой частичный порядок, что если a и b
принадлежат А, то либо aRb, либо bRa, либо a = b.
Если А — конечное множество, то линейный порядок R удобно представлять , считая все элементы множества А расположенными в виде последовательности
a1, a2,..., an,
для которой имеет место aiRaj тогда и только тогда, когда i < j.
Слайд 6
Если задан частичный порядок R на множестве А,
часто бывает нужен линейный порядок, содержащий этот частичный порядок.
Эта проблема вложения частичного порядка в линейный называется топологической сортировкой.
Формально можно сказать, что
частичный порядок R на множестве А
вложен в линейный порядок R',
если R‘ — линейный порядок и R⊆R',
т. е. aRb влечет aR'b для всех а и b из А.
Слайд 7
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
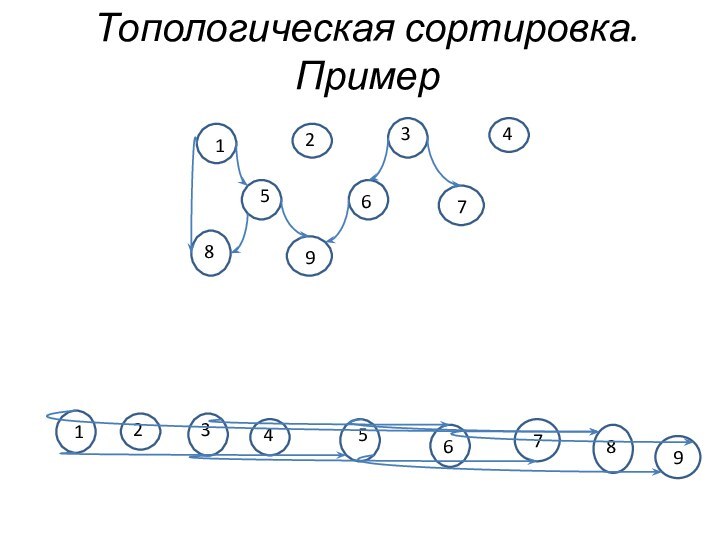
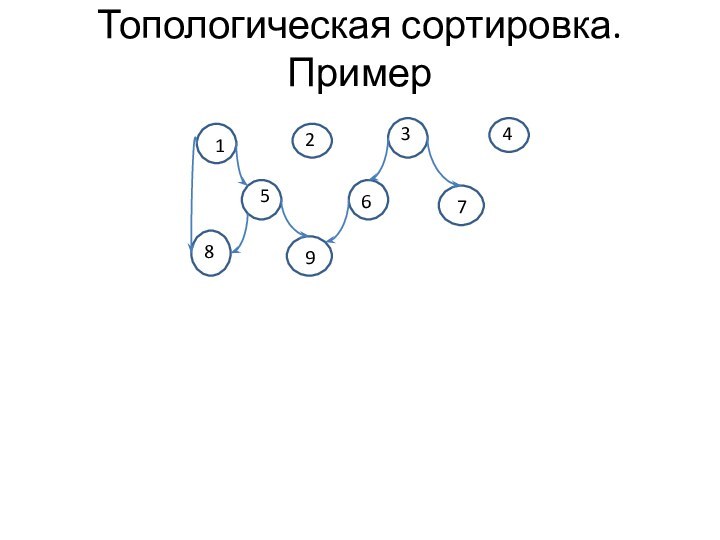
Топологическая сортировка. Пример
Слайд 8
Алгоритм. Топологическая сортировка
Вход. Частичный порядок R на конечном
множестве А.
Выход. Линейный порядок R' на А, для которого
R ⊆ R'.
Метод. Так как А — конечное множество, линейный порядок R' на А можно представить в виде списка On = a1, a2, ..., аn, для которого ai R' aj, если i < j, и А = {а1, a2, ..., аn}.
Эта последовательность элементов строится с помощью следующих шагов:
Положить i=1, АI=А и Ri=R.
Если Ai пусто, остановиться и выдать Оi = a1, ..., аi, в качестве искомого линейного порядка. В противном случае выбрать в Аi такой элемент аi+1 что a' R аi+1, ложно для всех a' ∈ Ai.
Положить Ai+1= Ai \ {аi+1} и Ri+1= Ri \ ({ai+1}×Ai+1). Затем увеличить i на единицу и повторить шаг 2.
Слайд 9
Топологическая сортировка. Пример
1
2
3
4
5
6
7
8
9
Слайд 10
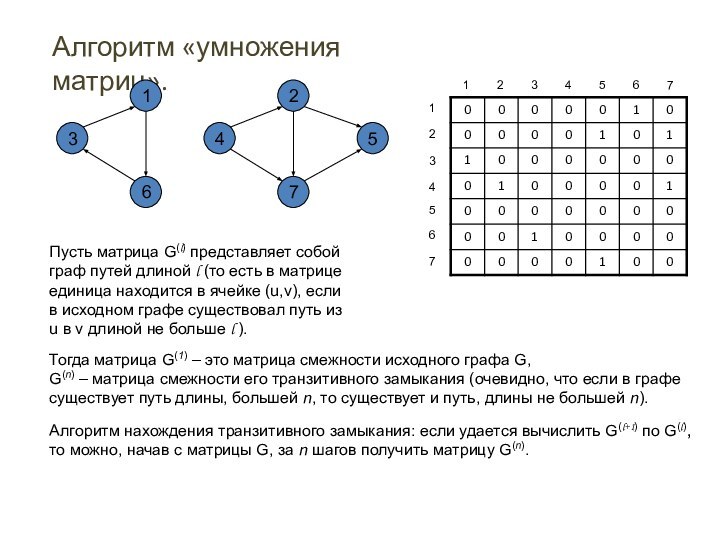
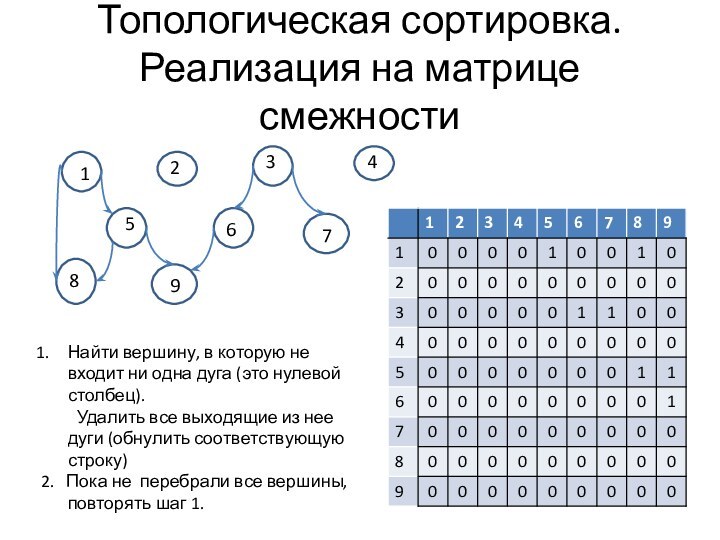
Топологическая сортировка. Реализация на матрице смежности
1
2
3
4
5
6
7
8
9
Найти вершину, в
которую не входит ни одна дуга (это нулевой столбец).
Удалить
все выходящие из нее дуги (обнулить соответствующую строку)
2. Пока не перебрали все вершины, повторять шаг 1.
Слайд 11
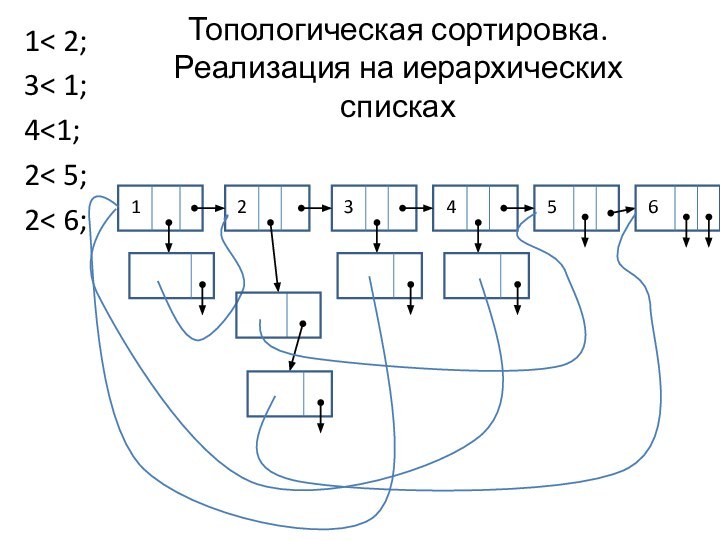
Топологическая сортировка.
Реализация на иерархических списках
1< 2;
3
1;
4
Слайд 12
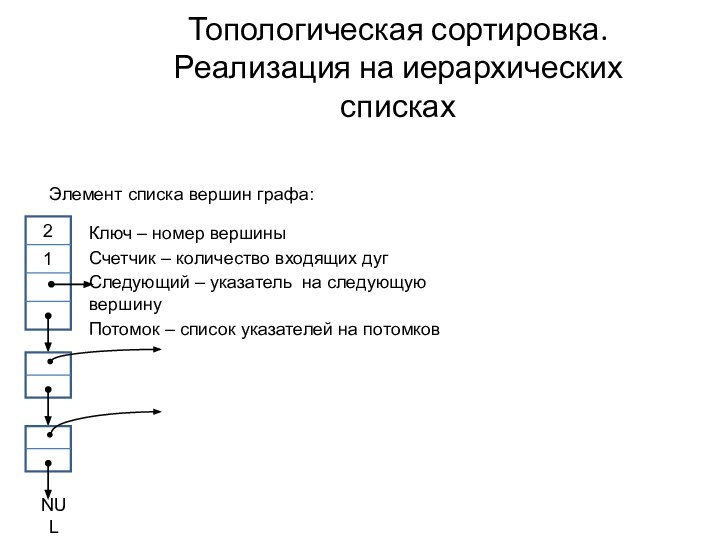
Топологическая сортировка.
Реализация на иерархических списках
2
1
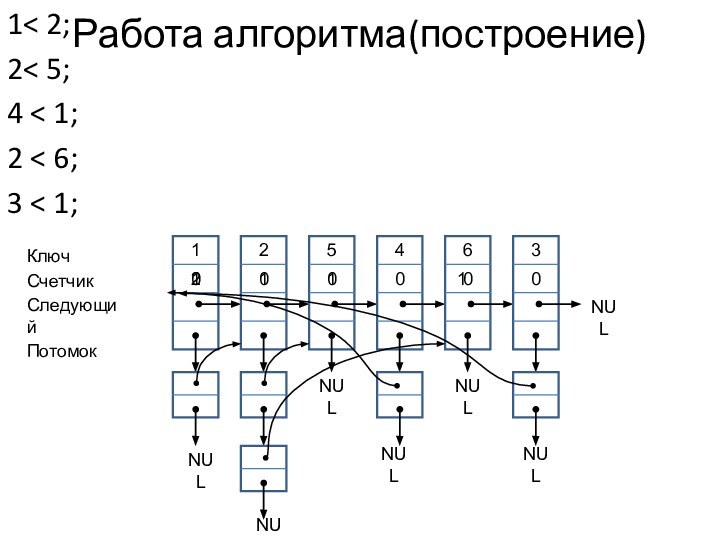
Ключ – номер
вершины
Счетчик – количество входящих дуг
Следующий – указатель на следующую
вершину
Потомок – список указателей на потомков
NUL
Элемент списка вершин графа:
Слайд 13
Работа алгоритма(построение)
1
2
2
1
5
1
4
0
6
1
3
0
Ключ
Счетчик
Следующий
Потомок
1
0
0
0
0
NUL
1< 2;
2< 5;
4 < 1;
2
6;
3 < 1;
NUL
NUL
NUL
NUL
NUL
NUL
Слайд 14
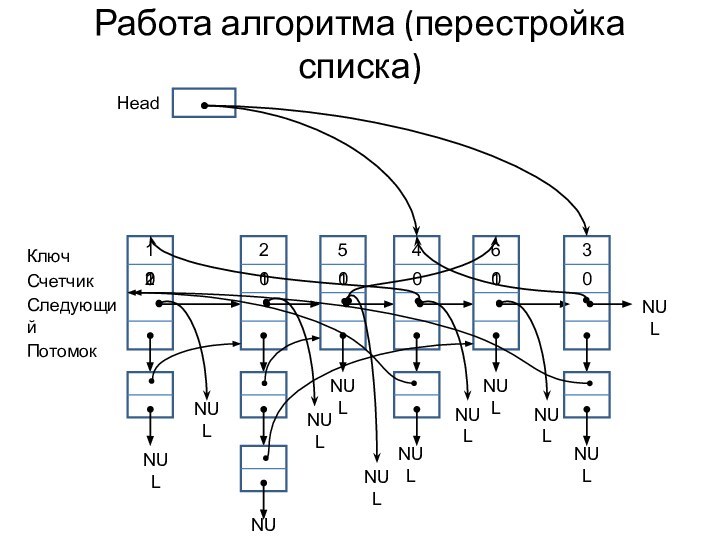
Работа алгоритма (перестройка списка)
1
2
2
1
5
1
4
0
6
1
3
0
Ключ
Счетчик
Следующий
Потомок
1
0
0
0
0
NUL
NUL
NUL
NUL
NUL
NUL
Head
NUL
NUL
NUL
NUL
NUL
NUL
Слайд 15
Кратчайшие пути
Пусть G = (V, E) – ориентированный
граф. Поставим в оответствие
каждому ребру e∈E в графе G
неотрицательную стоимость w (e).
w: E → R+ - функция стоимости
Стоимость (вес) пути p(v0, v1, … , vk) определяется как сумма
стоимостей ребер, входящих в этот путь: w(p) = ∑i w ( vi-1, vi ).
Вес кратчайшего пути из u в v равен по определению
min { w(p): u →p v }, если существует путь из u в v
δ(u,v)=
∞, иначе
Кратчайший путь из u в v это любой путь из u, для которого w(p)= δ(u,v)
Слайд 16
Ребра отрицательного веса
Веса ребер могут ребер могут быть
отрицательными.
Важно знать, имеются ли циклы отрицательного веса. Если
из вершины
s можно добраться до цикла отрицательного
веса, то можно обойти этот цикл сколь угодно раз, при этом
вес все время будет уменьшаться.
Для вершин этого цикла кратчайших путей не существует.
Если циклов отрицательного веса нет, то любой цикл можно
выбросить. Путей без циклов конечное число, так что вес
кратчайшего пути определен корректно.
Слайд 17
Пусть G = (V, E) – заданный граф.
Для каждой вершины v ∈ V мы будем помнить
ее предшественника.
Релаксация – постепенное уточнение верхней оценки на вес
кратчайшего пути в заданную вершину.
Свойства оптимальности.
Лемма 1. Отрезки кратчайших путей являются кратчайшими:
Если p(v1, v2, … , vk) – кратчайший путь из v1 в vk и 1 ≤ i ≤ j ≤ k,
то pij = (vi, vi+1, … , vj) есть кратчайший путь из vi в vj
Следствие 1. Рассмотрим кратчайший путь p из s в v. Пусть (u,v) –
последнее ребро этого пути. Тогда δ(s,v) = δ(s,u) + w(u,v).
Следствие 2. Для любого ребра (u,v) ∈ E справедливо
δ(s,v) ≤ δ(s,u) + w(u,v).
Слайд 18
Идея алгоритма нахождения кратчайших путей
из одной вершины
во все другие
Строится множество S, содержащее вершины
графа, кратчайшие расстояния
до которых от
источника известны.
На каждом шаге добавляется тот из оставшихся
узлов, кратчайшее расстояние до которого меньше
всех других оставшихся узлов.
Слайд 19
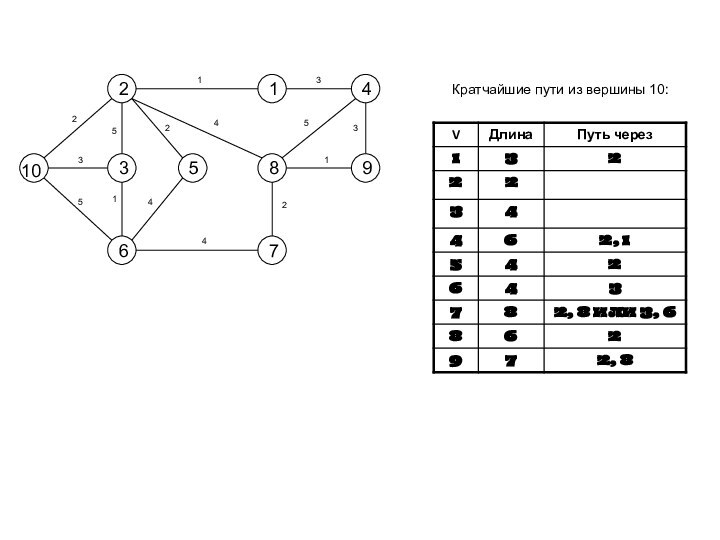
Кратчайшие пути из вершины 10:
10
Слайд 20
Техника релаксации
Для каждого ребра (u,v) храним d[v] –
верхнюю оценку
кратчайшего пути из s в v.
Initialize (G,s){
for (для ∀v ∈ V) {
d[v] ← ∞
Π[v] ← NULL;
}
d[s] ← 0;
}
Слайд 21
Релаксация ребра (u,v):
значение d[v] уменьшается до d[v+w(u,v)]
(если второе значение меньше первого)
Relax (u, v, w) {
If
(d[v] > d[u] + w(u,v)){
d[v] = d[ u] + w(u,v);
Π[v] ← u;
}
}
Слайд 22
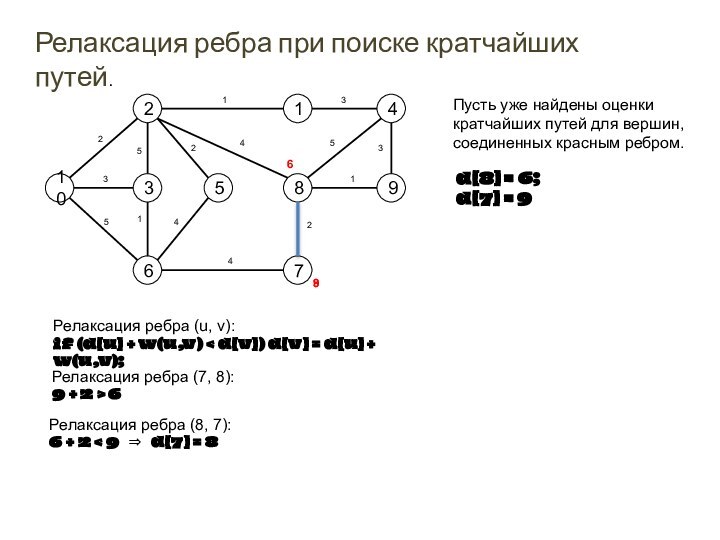
Релаксация ребра при поиске кратчайших путей.
10
2
3
6
1
8
5
7
4
9
1
1
1
2
2
2
3
4
3
3
4
4
5
5
5
Пусть уже найдены
оценки
кратчайших путей для вершин,
соединенных красным ребром.
9
6
d[8] = 6;
d[7] =
9
Релаксация ребра (u, v):
if (d[u] + w(u,v) < d[v]) d[v] = d[u] + w(u,v);
Релаксация ребра (7, 8):
9 + 2 > 6
Релаксация ребра (8, 7):
6 + 2 < 9 ⇒ d[7] = 8
8
Слайд 23
В ходе работы алгоритма поддерживается множество S,
состоящее из
вершин, для которых δ(s,v) уже найдено
( т.е. d[s,v]=
δ(s,v)).
Выбираем вершину u ∈V \ S c наименьшим d[u];
Добавляем вершину u к множеству S;
Выполняем релаксацию для всех инцидентных u ребер;
Пока в S не добавили все вершины, повторять шаги 1-3.
Слайд 24
Алгоритм Дейкстры
Dijkstra(G,w,s){
Initialize(G,s);
S ← ø;
Q ← V;
//очередь с приоритетами
While (Q ≠ ø){
u ← get(Q); //выбрать ближайшую
S ← S U {u};
for (для ∀v ∈ Adj[u])
Relax ( u, v, w);
}
}
Слайд 25
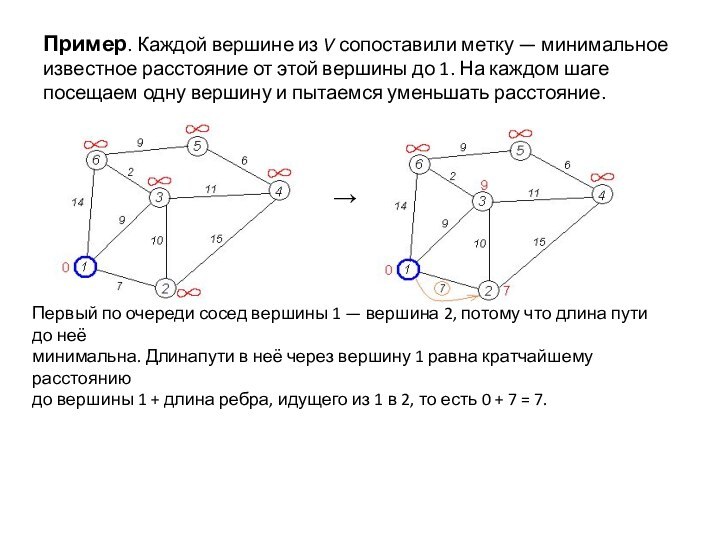
Пример. Каждой вершине из V сопоставили метку —
минимальное известное расстояние от этой вершины до 1. На
каждом шаге посещаем одну вершину и пытаемся уменьшать расстояние.
Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до неё
минимальна. Длинапути в неё через вершину 1 равна кратчайшему расстоянию
до вершины 1 + длина ребра, идущего из 1 в 2, то есть 0 + 7 = 7.
→
Слайд 26
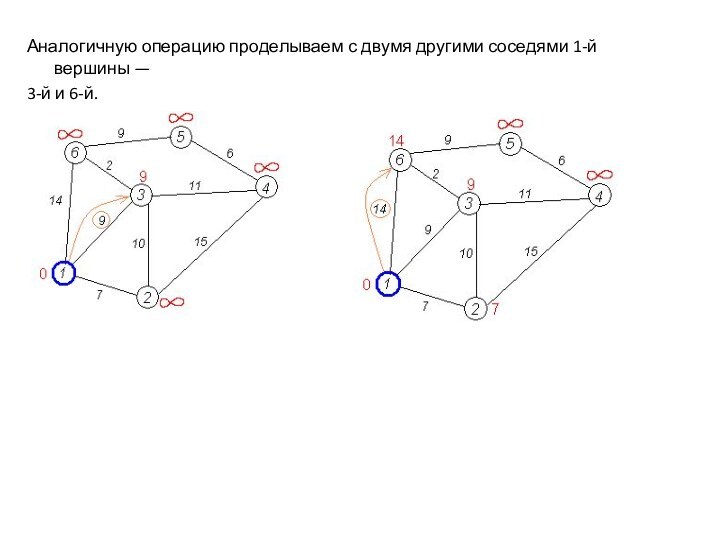
Аналогичную операцию проделываем с двумя другими соседями 1-й
вершины —
3-й и 6-й.
Слайд 27
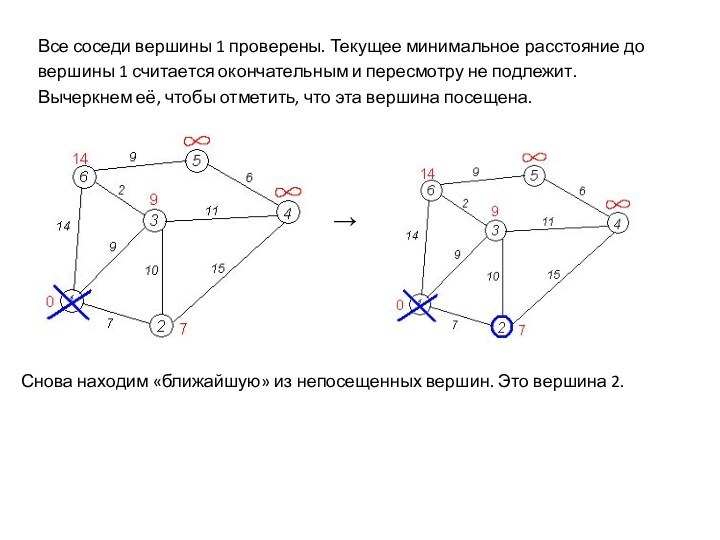
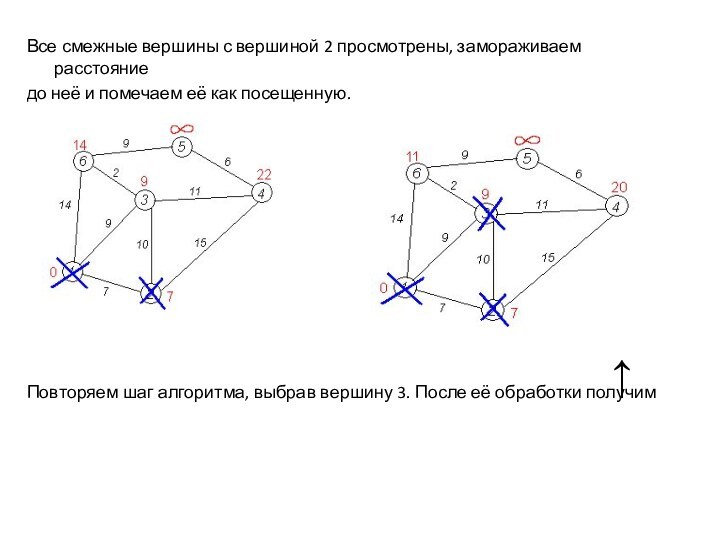
Все соседи вершины 1 проверены. Текущее минимальное расстояние
до
вершины 1 считается окончательным и пересмотру не подлежит.
Вычеркнем её, чтобы отметить, что эта вершина посещена.
Снова находим «ближайшую» из непосещенных вершин. Это вершина 2.
→
Слайд 28
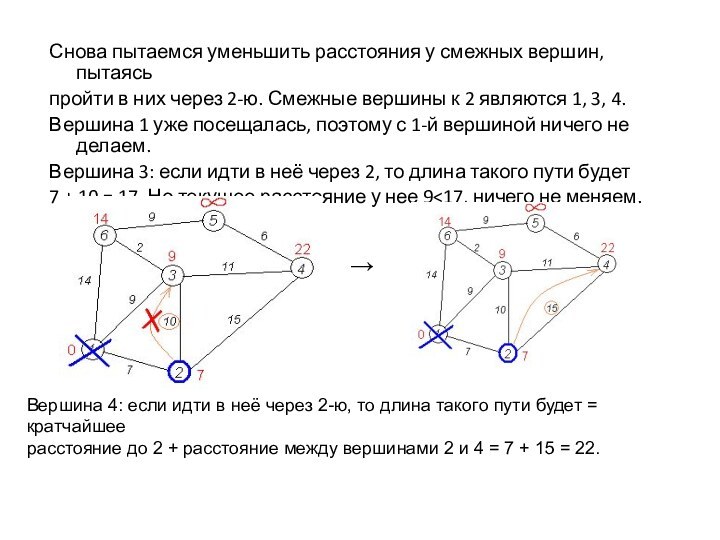
Снова пытаемся уменьшить расстояния у смежных вершин, пытаясь
пройти
в них через 2-ю. Смежные вершины к 2 являются
1, 3, 4.
Вершина 1 уже посещалась, поэтому с 1-й вершиной ничего не делаем.
Вершина 3: если идти в неё через 2, то длина такого пути будет
7 + 10 = 17. Но текущее расстояние у нее 9<17, ничего не меняем.
Вершина 4: если идти в неё через 2-ю, то длина такого пути будет = кратчайшее
расстояние до 2 + расстояние между вершинами 2 и 4 = 7 + 15 = 22.
→
Слайд 29
Все смежные вершины с вершиной 2 просмотрены, замораживаем
расстояние
до неё и помечаем её как посещенную.
Повторяем шаг алгоритма,
выбрав вершину 3. После её обработки получим
↑
Слайд 30
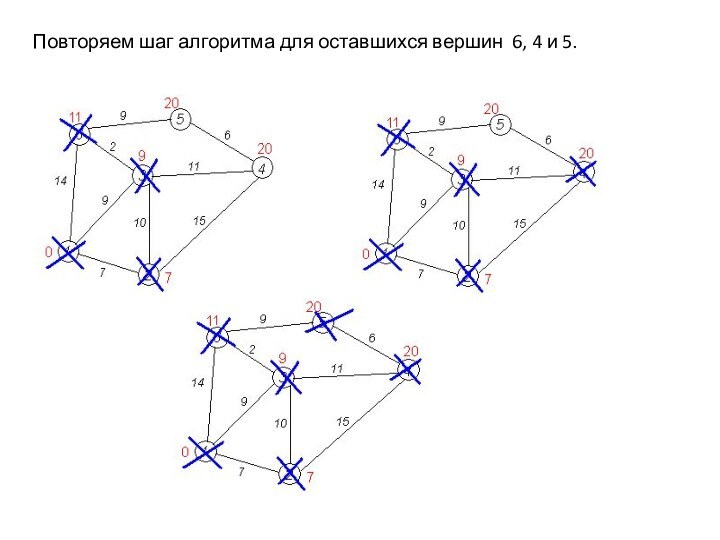
Повторяем шаг алгоритма для оставшихся вершин 6, 4
и 5.
Слайд 31
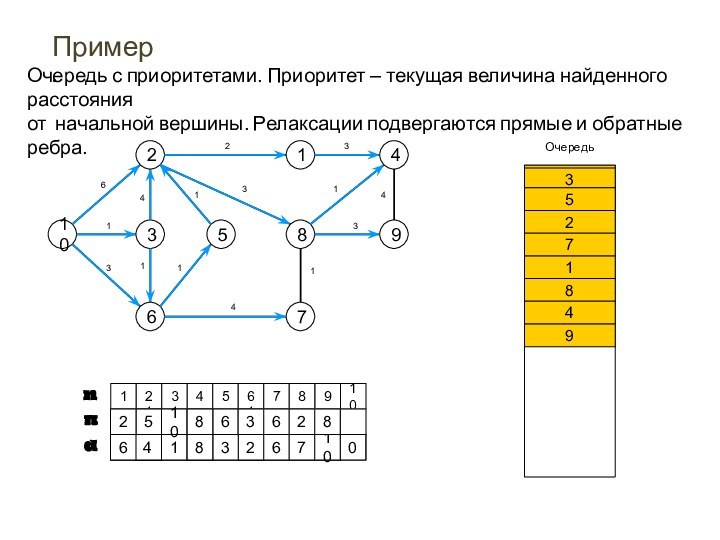
Пример.
Очередь с приоритетами. Приоритет – текущая величина найденного
расстояния
от начальной вершины. Релаксации подвергаются прямые и обратные
ребра.
10
2
3
6
1
8
5
7
4
9
2
3
1
1
1
6
3
1
4
1
3
4
4
3
1
6
10
2
3
6
3
1
6
10
10
10
5
2
3
3
5
7
6
3
6
4
5
6
7
2
2
1
8
1
9
4
10
8
9
8
8
Слайд 32
Реализация с дополнительным массивом - O(n2)
Массив D[v]
содержит стоимость текущего
кратчайшего пути из s в v.
Слайд 33
Dijkstra
{
S ← {s};
D[s] ← 0;
для всех v ∈V
\ {v0} выполнить: D[v] = w (s, v);
пока S
≠ V выполнять:
{
выбрать узел u ∈ V \ S, для которого
D[u] принимает наименьшее значение;
добавить w к S;
для всех v ∈V \ S выполнить
D[v] = min (D[v], D[u] + w(u, v));
}
}
Слайд 34
Пример
№ S u D[u] D[1] D[2] D[3] D[4]
0 {0} - - 2 +∞ +∞ 10
{0, 1} 1 2 2 5 +∞ 9
{0, 1,
2} 2 5 2 5 9 9
{0, 1, 2, 3} 3 9 2 5 9 9
4 {0, 1, 2, 3, 4} 4 9 2 5 9 9
0
2
1
4
3
2
3
4
5
10
7
6
Слайд 35
Сложность алгоритма Дейкстры зависит от способа нахождения вершины
v, а также способа хранения множества непосещенных вершин и
способа обновления расстояний.
В простейшем случае, когда для поиска вершины с минимальным d[v] просматривается все множество вершин, а для хранения величин d — массив, время работы алгоритма есть O(n2 + m). Основной цикл выполняется порядка n раз, в каждом из них на нахождение минимума тратится порядка n операций, плюс количество релаксаций, которое не превосходит количества ребер в исходном графе.
* Для разреженных графов непосещенные вершины можно хранить в двоичной куче, а в качестве ключа использовать значения d[i], тогда время извлечения вершины станет log n, при том, что время модификации d[i] возрастет до log n. Так как цикл выполняется порядка n раз, а количество релаксаций не больше m, скорость работы такой реализации O(nlogn + mlogn).
Слайд 36
* Если для хранения непосещенных вершин использовать фибоначчиеву
кучу, для которой удаление происходит в среднем за O(log
n), а уменьшение значения в среднем за O(1), то время работы алгоритма составит O(n log n + m).
Слайд 37
Алгоритм Беллмана — Форда
За время O(n × m)
алгоритм находит кратчайшие пути от
одной вершины графа до
всех остальных, допускает рёбра с
отрицательным весом. Предложен независимо Ричардом
Беллманом (Bellman) и Лестером Фордом (Ford).
Алгоритм маршрутизации RIP был впервые разработан в
1969 году, как основной для сети ARPANET.
В 1969 году Агентство передовых исследовательских
проектов (ARPA) предложило разработать компьютерную
сеть.
Слайд 38
Компьютерная сеть была названа ARPANET, все работы финансировались
за
счёт Министерства обороны США. Затем сеть ARPANET начала активно
расти
и развиваться, её начали использовать учёные из разных областей
науки. В 1973 году к сети были подключены первые иностранные
организации из Великобритании и Норвегии, сеть стала международной.
Стоимость пересылки электронного письма по сети ARPANET составляла
50 центов.
В 1984 году у сети ARPANET появился серьёзный соперник,
Национальный фонд науки США (NSF) основал обширную
межуниверситетскую сеть NSFNet, которая имела гораздо бо́льшую
пропускную способность (56 кбит/с), нежели ARPANET.
В 1990 году сеть ARPANET прекратила своё существование, полностью
проиграв конкуренцию NSFNet.
Слайд 39
Идея алгоритма
Алгоритм позволяет очень просто определить, существует ли
в
графе G отрицательный цикл, достижимый из вершины s.
Для проверки
нужно произвести внешнюю итерацию цикла
|V| раз. Если при исполнении последней итерации длина
кратчайшего пути до какой-либо вершины строго
уменьшилась, то в графе есть отрицательный цикл,
достижимый из s.
На основе этого можно предложить следующую
оптимизацию. Можно отслеживать изменения в графе и,
как только они закончатся, дальнейшие итерации будут
бессмысленны.
Слайд 40
Bellman-Ford(G,w,s) {
Initialize(G,s);
for(i=1; i
)
Relax(u,v,w);
for(∀ (u,v) ∈ E )
if (d[v]>d[u]+w(u,v)
return 0;
return
1;
}
Слайд 41
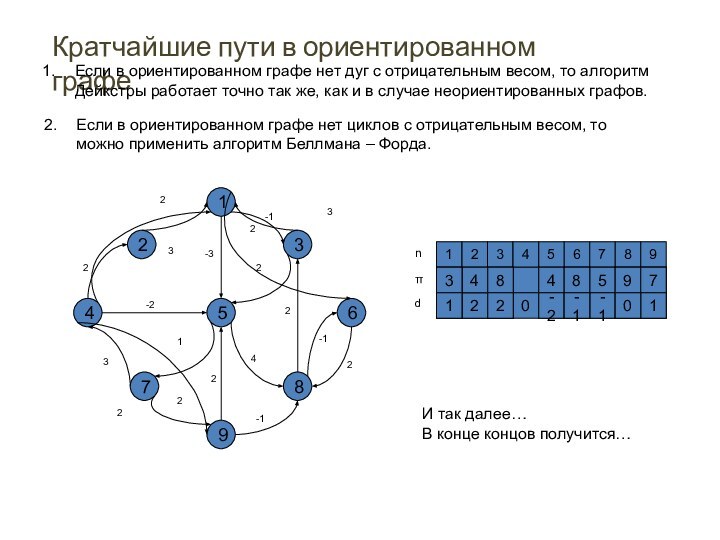
Кратчайшие пути в ориентированном графе
Если в ориентированном графе
нет дуг с отрицательным весом, то алгоритм
Дейкстры работает
точно так же, как и в случае неориентированных графов.
Если в ориентированном графе нет циклов с отрицательным весом, то
можно применить алгоритм Беллмана – Форда.
4
2
1
3
6
5
7
8
9
2
2
3
-3
2
-1
3
2
2
-1
2
4
-1
2
1
-2
3
2
2
2
4
4
3
4
-2
4
2
1
5
1
6
5
-1
5
2
9
1
7
1
8
3
8
0
0
И так далее…
В конце концов получится…
3
1
2
-1
Слайд 42
Нахождение кратчайших путей между всеми парами вершин
Строим матрицу
стоимостей:
w(i, j), если ребро (i, j)∈E
M[i, j] = +∞
, если ребро (i, j)∉E
0, если i = j
Обозначим через d [i, j] матрицу кратчайших
путей между всеми вершинами.
Вершины занумеруем числами от 1 до n.
Слайд 43
Алгоритм Флойда-Уоршолла
Обозначим через dij(k) стоимость кратчайшего пути из
вершины с номером i в вершину с номером j
с промежуточными вершинами из множества {1, 2, …, k}.
M[i, j] , если k = 0,
dij(k) =
min(dij(k-1) , dik(k-1) + dkj(k-1) ), если k≥1
D(n) содержит искомое решение
Слайд 44
Floyd-Warshall(M, n) {
D(0) ← M;
for k ← 1
to n do
for i ←1 to n do
for j ← 1 to n do
dij(k) ← min(dij(k-1), dik(k-1) + dkj(k-1) );
return D(n);
}
Слайд 45
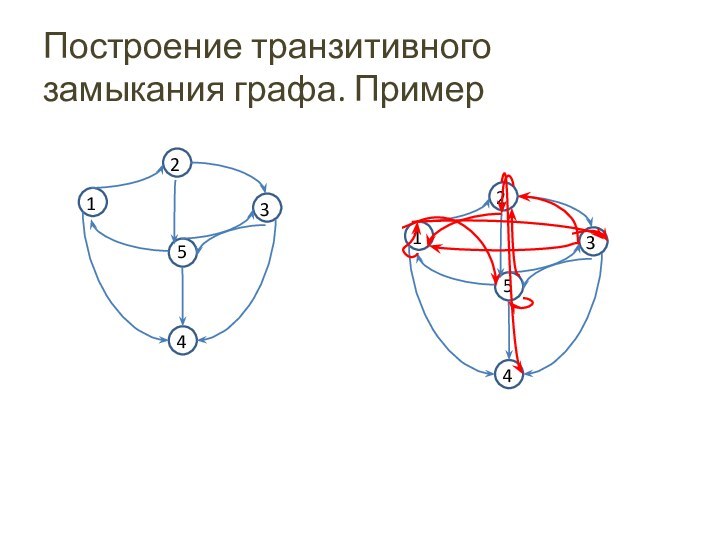
Транзитивное замыкание графа
Пусть G= (V, E) ориентированный граф.
Транзитивным замыканием графа G называется граф G’= (V, E’),
в котором из вершины v в вершину w идет ребро ⇔ существует путь (длины 0 или больше) из v в w в графе G.
E’:
(a, b)∈E & (b, c) ∈ E ⇒ (a, b)∈E’ & (b, c) ∈ E’ & (a, c) ∈ E’
Слайд 46
Построение транзитивного замыкания графа. Пример
1
3
2
5
4
1
3
2
5
4
Слайд 47
Обозначим через tij(k) наличие пути из вершины с
номером i в вершину с номером j с промежуточными
вершинами из множества {1, 2, …, k}. M – матрица смежностей графа G.
M[i, j] , если k = 0,
tij(k) =
tij(k-1) ∨ (tik(k-1) ∧ tkj(k-1) ), если k≥1
T(n) содержит искомое решение.
Слайд 48
Алгоритм построения транзитивного замыкания графа
Tranzitive_Closure(M, n)
{
T(0) ← M;
for
k ← 1 to n do
for i ←1
to n do
for j ← 1 to n do
tij(k) ← tij(k-1) ∨ (tik(k-1) ∧ tkj(k-1) );
return T(n);
}
Слайд 49
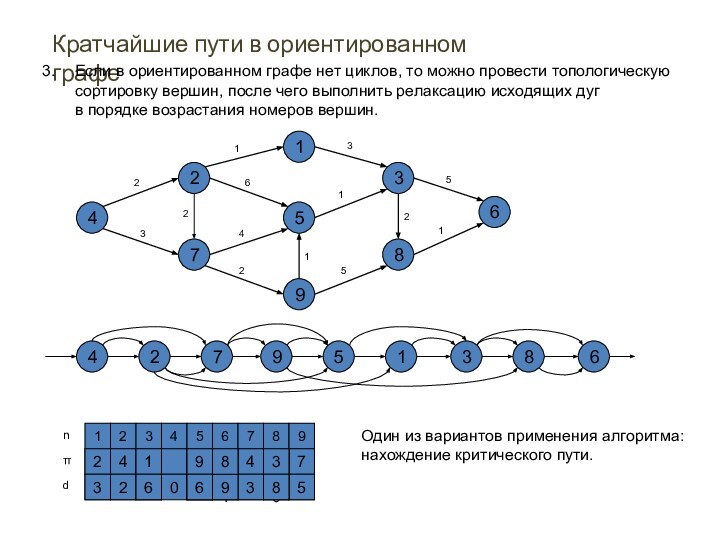
Кратчайшие пути в ориентированном графе
Если в ориентированном графе
нет циклов, то можно провести топологическую
сортировку вершин, после чего
выполнить релаксацию исходящих дуг
в порядке возрастания номеров вершин.
1
5
9
2
7
3
8
4
6
2
1
3
5
1
6
2
3
4
2
5
2
1
1
11
4
4
2
3
2
3
7
5
9
10
5
7
1
6
3
8
3
9
8
2
8
7
7
9
6
Один из вариантов применения алгоритма:
нахождение критического пути.










![Топологическая сортировка, пути в графе Техника релаксацииДля каждого ребра (u,v) храним d[v] – верхнюю оценкукратчайшего пути из](/img/tmb/15/1458769/bff0e6eac60afeb2d14c9da9a4185134-720x.jpg)
![Топологическая сортировка, пути в графе Релаксация ребра (u,v): значение d[v] уменьшается до d[v+w(u,v)] (если второе значение меньше](/img/tmb/15/1458769/233b8bb4bc8df3c453a1e5afee3c89e8-720x.jpg)


![Топологическая сортировка, пути в графе Реализация с дополнительным массивом - O(n2) Массив D[v] содержит стоимость текущего кратчайшего](/img/tmb/15/1458769/53c38555115d63f2adff16c45a4f0d2f-720x.jpg)
![Топологическая сортировка, пути в графе Dijkstra{ S ← {s}; D[s] ← 0; для всех v ∈V \ {v0} выполнить: D[v]](/img/tmb/15/1458769/5592708b29f2668ec35206fdfff320f1-720x.jpg)
![Топологическая сортировка, пути в графе Пример№ S u D[u] D[1] D[2] D[3] D[4]0 {0} - - 2 +∞ +∞ 10{0, 1} 1 2 2 5 +∞ 9{0, 1, 2} 2 5 2 5 9 9{0, 1, 2, 3} 3 9 2 5 9 94](/img/tmb/15/1458769/c26f74d6f40bd0b87a85a1047af80ddf-720x.jpg)





![Топологическая сортировка, пути в графе Bellman-Ford(G,w,s) { Initialize(G,s); for(i=1; id[u]+w(u,v) return 0; return 1;}](/img/tmb/15/1458769/15cadf0bf06573b13c2ebd63d54b58d6-720x.jpg)