Презентация на тему Учебно-исследовательские технологии обучения математике

увлекательного и интересного , найти подтверждение применения ленты Мёбиуса

в современном мире.

Задачи:

Расширить сферу математических знаний: познакомиться с лентой Мёбиуса;
Расширить кругозор посредством знакомства с образцами произведения искусства и разнообразным применением ленты Мёбиуса в реальной жизни.

результате проведенного исследования и экспериментальной работы с последующей статистической

обработкой было выяснено, что лента Мёбиуса встречается в различных сферах жизнедеятельности человека и является ценным открытием не только в России, и во всем мире.

Методы исследования:
анализ литературы по проблеме исследования;
сбора эмпирических данных, наблюдение, эксперименты, обработка данных.
Изучались свойства ленты на наглядных примерах

Математика постоянно живёт и развивается!

математик и астроном-теоретик. Родился в городе Шульпфорте, профессор Лейпцигского

университета с 1816 года. Установил существование односторонних поверхностей (1858г.) одна из которых – лента Мёбиуса. Лента Мёбиуса была открыта независимо немецкими математиками Августом Фердинандом Мёбиусом и Иоганном Бенедиктом Листингом(немецкий математик и физик).

В возрасте 68 лет Мёбиусу удалось сделать открытие поразительной красоты.

Что же такое Лента Мёбиуса? И в чем её особенность?

ленты Мёбиуса
Если разрезать  ленту Мёбиуса,  не посередине, а отступая

от края приблизительно на треть её ширины, то получатся две сцепленные  ленты, одна — более короткая лента Мёбиуса, и  другая — длинная лента  Мёбиуса  с двумя полуоборотами. Разрез ленты с дополнительными оборотами дал неожиданные фигуры, они  называются  парадромными кольцами.

с муравьями принадлежит
известному голландскому художнику
Морису Эшеру


Свойства ленты

Мёбиуса

Если покрасить Ленту Мёбиуса, не переворачивая, то она закрасится полностью.

Полный обход вокруг листа изменяет направление окружности на противоположное. Это говорит о том, что поверхность листа Мёбиуса не ориентируема ( поверхность допускающая ориентацию).

из объектов области математики под названием «топология» («геометрия положений»)
Топология

известна и под именем «резиновая геометрия», потому что топологу ничего не стоит поместить все свои фигуры на поверхности детского надувного шарика и без конца менять его форму, следя лишь за тем ,чтобы шарик не лопнул. А то, что при этом прямые линии, например стороны треугольника, превратятся в кривые, для тополога глубоко безразлично.

Что общего между листом бумаги, поверхностью стола, бубликом и кружкой? Конечно, можно, сидя за столом, съесть бублик, лежащий на бумажке, и запить молоком из кружки. Но между ними имеется и более тесная связь: с точки зрения геометрии их поверхности абсолютно одинаковы.

кристаллов
Жидкие кристаллы являются одним из самых важных элементов современной

жизни. С большим процентом вероятности, вы сейчас читаете эти строки благодаря именно жидким кристаллам, точнее их способности модулировать свет, которая используется для изготовления плоских экранов дисплеев компьютеров, планшетов, смартфонов, телевизоров и других электронных устройств.

Лента Мёбиуса с одним поворотом вызывает интересное искажение ориентации жидких кристаллов, однако ленты с тремя, четырьмя и пятью поворотами заставляют жидкие кристаллы завязаться в сложные узлы, в узел трилистника, узел Соломона и узел пятилистника соответственно.

в частности, отражение в зеркале – это своеобразный перенос

во времени. Несмотря на то, что Мёбиус сделал своё удивительное открытие давно, оно очень популярно и в наши дни: а у математиков идут дальнейшие исследования.

Есть гипотеза, что спираль ДНК сама по себе тоже является фрагментом ленты Мёбиуса. Более того, такая структура вполне логично объясняет причину наступления биологической смерти – спираль замыкается сама на себя и происходит самоуничтожение.

Еще один таинственный символ – знак бесконечности в виде “лежащей восьмерки” был найден в центре нашей галактики – Млечного пути. “Восьмерка” протяженностью в 600 световых лет состоит из плотного газа.

горки», ленточный конвейер …Китайские мастера добавили еще одно "измерение"

- использования , когда в сознании визуализируются и воображаются ряды специальных последовательных цифр ( особым дизайном исполнением) на фоне такой воображаемой ленте Мёбиуса. Эффект методики - саморегуляция, исцеление от болезней, развитие способностей человека, рост его духовности...
Такая практика существует и у сибирских шаманов уже много тысячелетий, т.к. Петля Мёбиус всегда над головой - северное сияние в атмосфере ночи... Осуществляют Великое путешествие шамана в Верхние и Нижние миры Мироздания...

Мёбиуса), ведь точно так же выглядит и аура человека

на вопрос: движется ли человек вверх?
Невозможный треугольник – трибар,

придуманный английским математиком Роджером Пенроузом в 1954 году. Что же невозможного в этой фигуре? С первого взгляда трибар кажется просто изображением равностороннего треугольника. Но стороны, сходящиеся вверху рисунка, кажутся перпендикулярными. В тоже время левая и правая грани внизу тоже кажутся перпендикулярными. Если смотреть на каждую деталь отдельно, то она кажется реальной, но, в общем, эта фигура существовать не может. Она не деформирована, но при черчении были неправильно соединены правильные элементы.

Водопад

Компьютерная модель вечного двигателя Эшера.

направлении. Лента Мёбиуса же, вопреки всем законам, направление срабатывания

не меняет, подобно механизмам с двумя устойчивыми положениями. Такая пружина могла бы стать бесценной в заводных игрушках – её нельзя перекрутить, как обычную – своего рода вечный двигатель. В 1971 году изобретатель с Урала Чесноков П.Н. применил фильтр в виде ленты Мёбиуса.

Лента Мёбиуса используется в кулинарии для того, чтобы создать интересный и аппетитный вид для булочек, сушек, хвороста. А также при изготовлении инструментов для приготовления и украшения различных блюд, силовых конструкций (мешалка).

удалось свернуть в форме ленты Мёбиуса одиннадцать расположенных параллельно

друг другу спиралей ДНК.

В 1967 году в Бразилии на международном математическом конгрессе выпустили памятную марку достоинством в пять сентаво.

Международный Символ переработки

Лента Мёбиуса – это воплощение многих важных духовных идей, известных в сакральной геометрии (учение о формах Пространства и закономерностях развития Вселенной в соответствии с этими формами).

Кинолента М атричный принтер

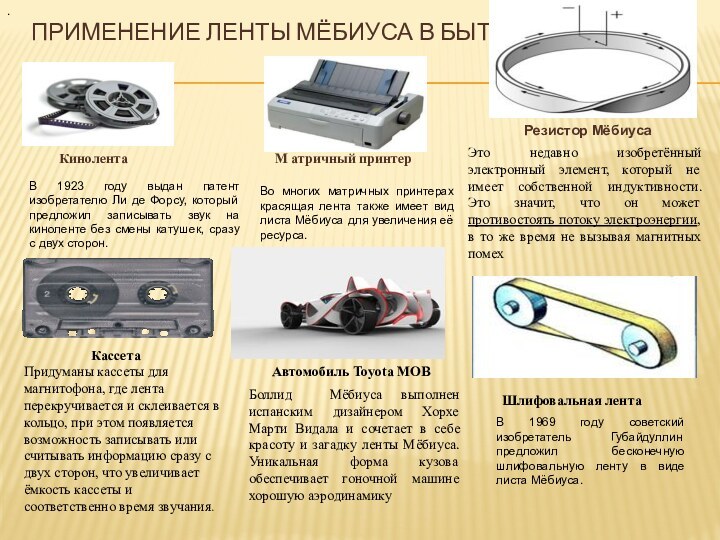
В 1923 году выдан патент изобретателю Ли де Форсу, который предложил записывать звук на киноленте без смены катушек, сразу с двух сторон. 

Во многих матричных принтерах красящая лента также имеет вид листа Мёбиуса для увеличения её ресурса. 

Резистор Мёбиуса

.

Это недавно изобретённый электронный элемент, который не имеет собственной индуктивности. Это значит, что он может противостоять потоку электроэнергии, в то же время не вызывая магнитных помех

Шлифовальная лента

В 1969 году советский изобретатель Губайдуллин предложил бесконечную шлифовальную ленту в виде листа Мёбиуса.
 

Автомобиль Toyota MOB

Кассета

Боллид Мёбиуса выполнен испанским дизайнером Хорхе Марти Видала и сочетает в себе красоту и загадку ленты Мёбиуса. Уникальная форма кузова обеспечивает гоночной машине хорошую аэродинамику

Придуманы кассеты для магнитофона, где лента перекручивается и склеивается в кольцо, при этом появляется возможность записывать или считывать информацию сразу с двух сторон, что увеличивает ёмкость кассеты и соответственно время звучания.

виде ленты Мёбиуса. Поговаривают, что придумал свою ленту Август

Фердинанд Мёбиус, когда наблюдал за горничной, которая надевала на шею шарф. Для изготовления такого шарфа достаточно соединить концы обычного шарфа в кольцо, предварительно перевернув один из них на изнаночную сторону. Шарф Мебиус – вещь внесезонная.

архитектуры
В мире немало памятников и построек ленте Мёбиуса
Проект

библиотеки в Казахстане

В Минске

Памятник в Москве