Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

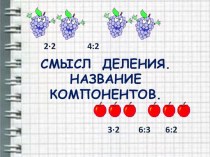
Презентация на тему Урок-общественный смотр значений по математике

Содержание

2. Цели урока: обобщить и
3. Правила работы в группеВыбрать капитана.Капитаны по ходу
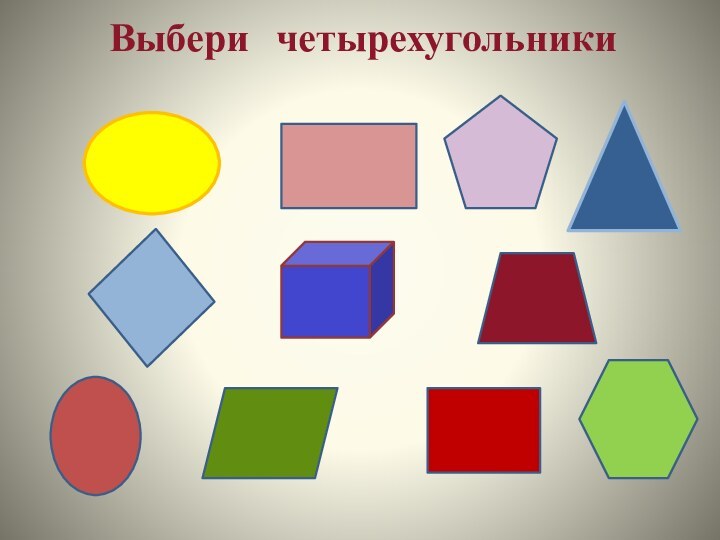
4. Выбери четырехугольники
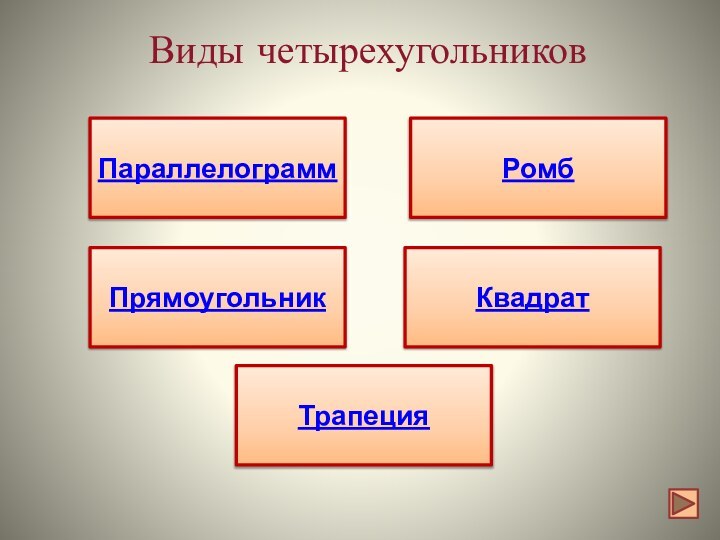
5. Виды четырехугольниковПараллелограммРомбПрямоугольникКвадратТрапеция
6. ПараллелограммСвойстваЧетырехугольник, у которогопротивоположные стороны попарно параллельныДиагонали точкой
7. Ромб
8. ПрямоугольникПараллелограмм, у которого все углы прямыеСвойстваДиагонали точкой
9. КвадратПараллелограмм, у которого все углы прямые и
10. ТрапецияЧетырехугольник, у которого две стороны параллельны, а
11. На рисунке ABCD параллелограмм, причем АВ ≠
12. ОфтальмотренажерУпражнения для глаз:вертикальные движения глаз вверх
13. Задача: oдна из сторон параллелограмма в 5
14. Задача: диагонали прямоугольника ABCD пересекаются в
15. Задача: один из углов ромба ABCD на
16. Задача: в квадрате проведены диагонали. 1) Докажите,
17. Задача: в равнобедренной трапеции DEFC на большее
18. В свободную минуткуГреческий крест разрежьте на несколько частей, из которых можно сложить квадрат
19. Комплекс упражнений «Танцуйте сидя»
20. Творческое заданиеИгра «Поле чудес»Знаешь ли ты?
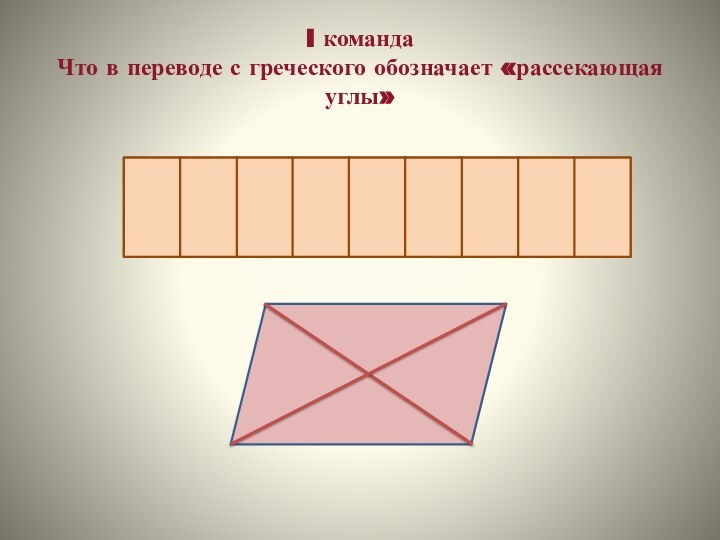
21. I команда Что в переводе с греческого обозначает «рассекающая углы»ДЬЛААИГОН
22. II команда Что в переводе с греческого обозначает «земледелие»ИРТЕГОМЕЯ
23. III команда Что в переводе с греческого обозначает «бубен»РОМБ
24. IV команда Что в переводе с греческого обозначает «столик»ЯИЦРТАПЕ
25. V команда Он фигура замечательная: как его не поверни, все четыре стороны у него равныТАРКВАД
26. Критерии итоговой отметки 7-6 балов –
27. Домашнее заданиеПодготовка к контрольной работе: вопросы к
28. Образование есть то, что остается, когда всевыученное уже забыто М.Лауэ
29. Рефлексия сегодня я узнал…
30. Проверка настроенияРавнодушноеОтличноеПлохое
31. Спасибо за урокСпасибо всем за работу !
32. Скачать презентацию
33. Похожие презентации

Цели урока: обобщить и систематизировать теоретические знания по теме "Четырехугольники";совершенствовать навыки решения задач по данной теме;развивать грамотную математическую речь.

Главная
Математика
Урок-общественный смотр значений по математике

Урок- общественный смотр знаний по теме: «Четырехугольники» 8 классп. Сафоново-1 Мурманская областьМБОУ СОШ №5Сивожелезова Т.С.

Цели урока: обобщить и систематизировать теоретические знания по теме

Правила работы в группеВыбрать капитана.Капитаны по ходу урока заполняют оценочные листы для

Виды четырехугольниковПараллелограммРомбПрямоугольникКвадратТрапеция

ПараллелограммСвойстваЧетырехугольник, у которогопротивоположные стороны попарно параллельныДиагонали точкой пересечения делятся пополамДиагонали равныВсе стороны

ПрямоугольникПараллелограмм, у которого все углы прямыеСвойстваДиагонали точкой пересечения делятся пополамДиагонали равныДиагонали перпендикулярны,

КвадратПараллелограмм, у которого все углы прямые и стороны равныСвойстваДиагонали точкой пересечения делятся

ТрапецияЧетырехугольник, у которого две стороны параллельны, а две другие стороны не параллельныСвойства

На рисунке ABCD параллелограмм, причем АВ ≠ ВС, KMNP- ромб. Укажите номера

ОфтальмотренажерУпражнения для глаз:вертикальные движения глаз вверх – вниз (4-6 раз); 2)

Задача: oдна из сторон параллелограмма в 5 раз больше другой. Найдите длину

Задача: диагонали прямоугольника ABCD пересекаются в точке О. Найдите периметр треугольника

Задача: один из углов ромба ABCD на 40 ̊ больше другого. Найдите

Задача: в квадрате проведены диагонали. 1) Докажите, что при этом он разбивается

Задача: в равнобедренной трапеции DEFC на большее основание DC проведены перпендикуляры ЕА

В свободную минуткуГреческий крест разрежьте на несколько частей, из которых можно сложить квадрат

Комплекс упражнений «Танцуйте сидя» Мы все вместе улыбнемся,

Творческое заданиеИгра «Поле чудес»Знаешь ли ты?

I команда Что в переводе с греческого обозначает «рассекающая углы»ДЬЛААИГОН

II команда Что в переводе с греческого обозначает «земледелие»ИРТЕГОМЕЯ

III команда Что в переводе с греческого обозначает «бубен»РОМБ

IV команда Что в переводе с греческого обозначает «столик»ЯИЦРТАПЕ

V команда Он фигура замечательная: как его не поверни, все четыре стороны у него равныТАРКВАД

Критерии итоговой отметки 7-6 балов – «5» 5- 4 бала

Домашнее заданиеПодготовка к контрольной работе: вопросы к главе II стр.160; карточки с

Образование есть то, что остается, когда всевыученное уже забыто М.Лауэ

Рефлексия сегодня я узнал… было интересно…

Проверка настроенияРавнодушноеОтличноеПлохое

Литература Геометрия 7-9 классы. Л.С. АтанасянКонтрольные работы по геометрии 8 класс

Слайды презентации

Слайд 2 Цели урока:
обобщить и систематизировать теоретические знания

по теме "Четырехугольники";
совершенствовать навыки решения задач по данной теме;
развивать

грамотную математическую речь.

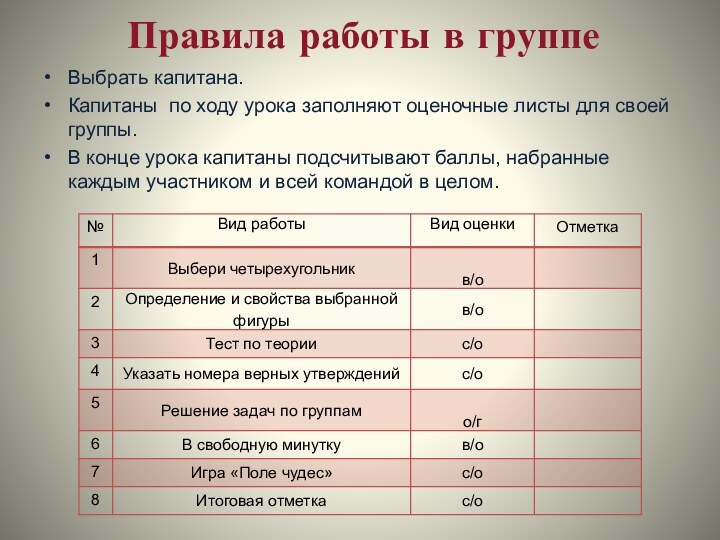
Слайд 3 Правила работы в группе
Выбрать капитана.
Капитаны по ходу урока

Правила работы в группеВыбрать капитана.Капитаны по ходу урока заполняют оценочные листы

заполняют оценочные листы для своей группы.
В конце урока капитаны

подсчитывают баллы, набранные каждым участником и всей командой в целом.

Слайд 4 Выбери четырехугольники

Слайд 5 Виды четырехугольников
Параллелограмм
Ромб
Прямоугольник
Квадрат
Трапеция

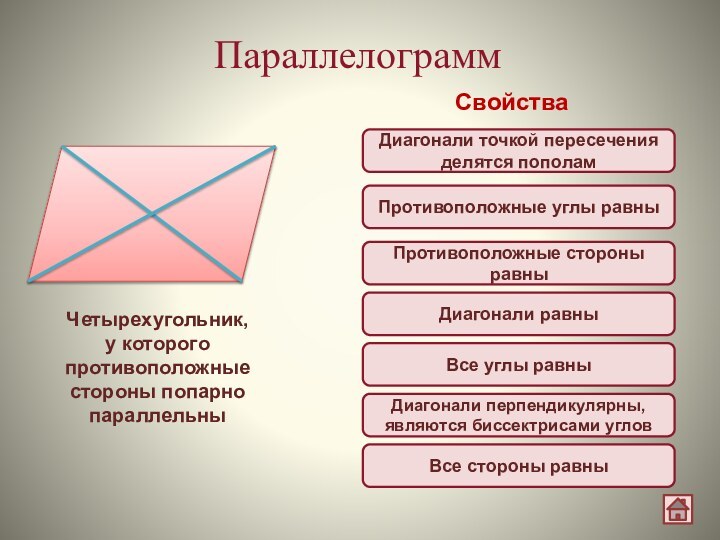
Слайд 6 Параллелограмм
Свойства

Четырехугольник,
у которого
противоположные стороны попарно параллельны

Диагонали точкой пересечения

делятся пополам

Диагонали равны

Все стороны равны

Диагонали перпендикулярны, являются биссектрисами углов

Все

углы равны

Противоположные стороны равны

Противоположные углы равны

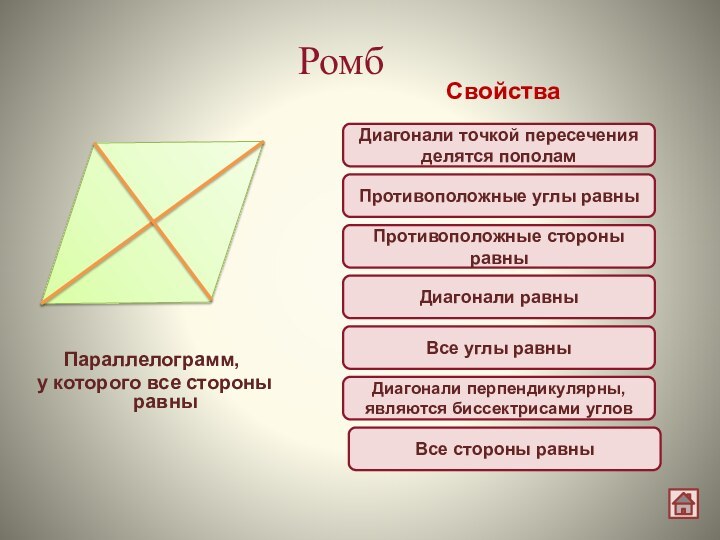
Слайд 7 Ромб

Параллелограмм,
у которого все стороны равны

Свойства

Диагонали точкой пересечения делятся пополам

Диагонали равны

Все стороны равны

Диагонали перпендикулярны, являются биссектрисами углов

Все углы равны

Противоположные стороны равны

Противоположные углы равны

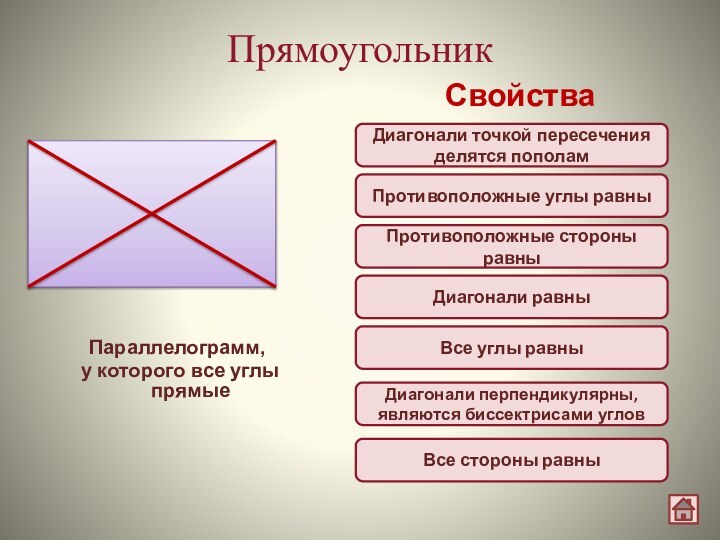
Слайд 8 Прямоугольник

Параллелограмм,
у которого все углы прямые
Свойства

Диагонали точкой пересечения

делятся пополам

Диагонали равны

Диагонали перпендикулярны, являются биссектрисами углов

Все углы равны

Противоположные

стороны равны

Все стороны равны

Противоположные углы равны

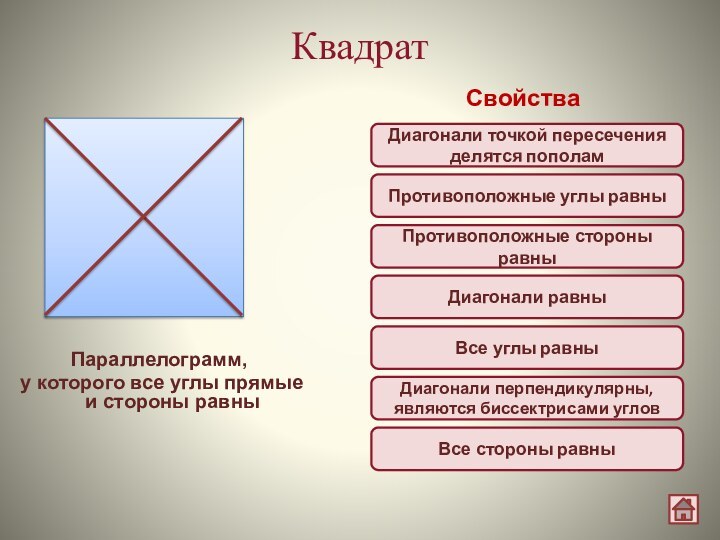
Слайд 9 Квадрат

Параллелограмм,
у которого все углы прямые и стороны

КвадратПараллелограмм, у которого все углы прямые и стороны равныСвойстваДиагонали точкой пересечения

равны

Свойства

Диагонали точкой пересечения делятся пополам

Диагонали равны

Все стороны равны

Диагонали перпендикулярны,

являются биссектрисами углов

Все углы равны

Противоположные стороны равны

Противоположные углы равны

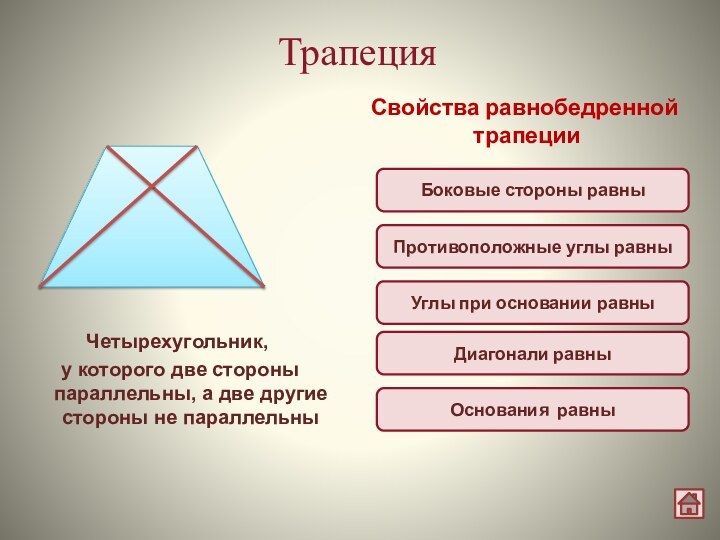
Слайд 10 Трапеция
Четырехугольник,
у которого две стороны параллельны, а две

ТрапецияЧетырехугольник, у которого две стороны параллельны, а две другие стороны не

другие стороны не параллельны
Свойства равнобедренной
трапеции

Противоположные углы равны

Боковые стороны

равны

Углы при основании равны

Диагонали равны

Основания равны

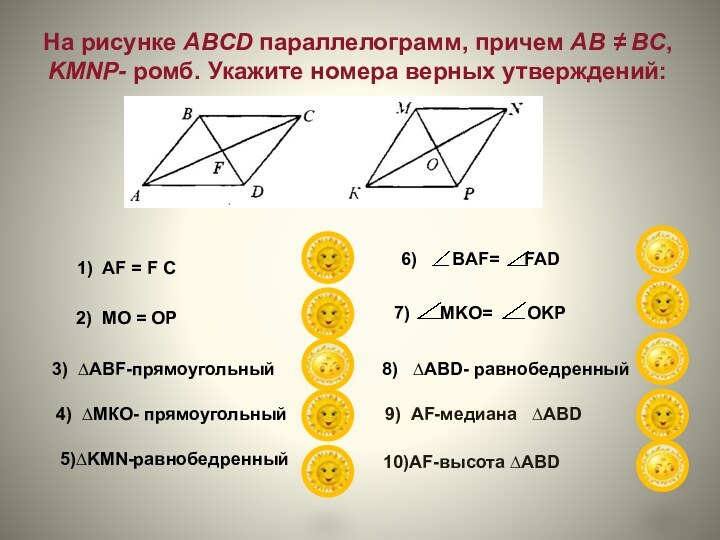
Слайд 11 На рисунке ABCD параллелограмм, причем АВ ≠ ВС,

На рисунке ABCD параллелограмм, причем АВ ≠ ВС, KMNP- ромб. Укажите

KMNP- ромб. Укажите номера верных утверждений:
1) AF = F

2) MO = OP

3) ∆ABF-прямоугольный

4) ∆МКО- прямоугольный

5)∆KMN-равнобедренный

6) BAF= FAD

7) MKO= OKP

8) ∆ABD- равнобедренный

9) AF-медиана ∆ABD

10)AF-высота ∆ABD

Слайд 12 Офтальмотренажер
Упражнения для глаз:

вертикальные движения глаз
вверх –

вниз (4-6 раз);

2) горизонтальное
вправо –

влево (4-6 раз);

3) вращение глазами по часовой стрелке и против часовой стрелки;

4) закрыть глаза и представить по очереди цвета радуги как можно отчетливее;

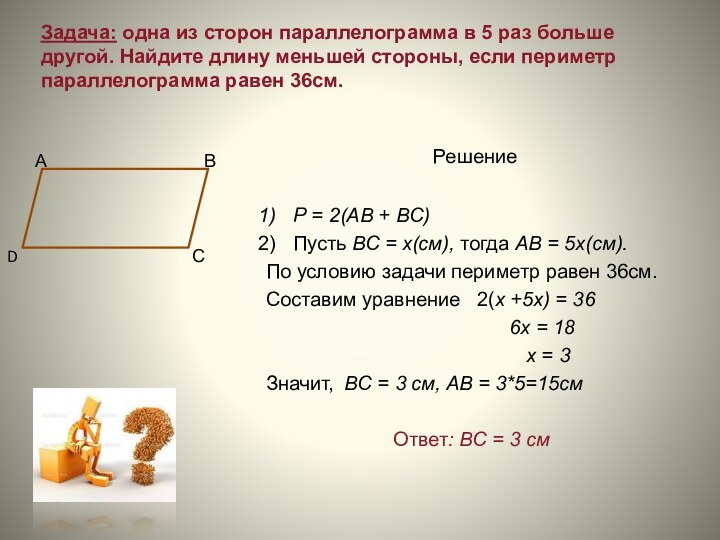
Слайд 13 Задача: oдна из сторон параллелограмма в 5 раз

Задача: oдна из сторон параллелограмма в 5 раз больше другой. Найдите

больше другой. Найдите длину меньшей стороны, если периметр параллелограмма

равен 36см.

Решение

Р = 2(АВ + ВС)
Пусть ВС = х(см), тогда АВ = 5х(см).
По условию задачи периметр равен 36см.
Составим уравнение 2(х +5х) = 36
6х = 18
х = 3
Значит, ВС = 3 см, АВ = 3*5=15см

Ответ: ВС = 3 см

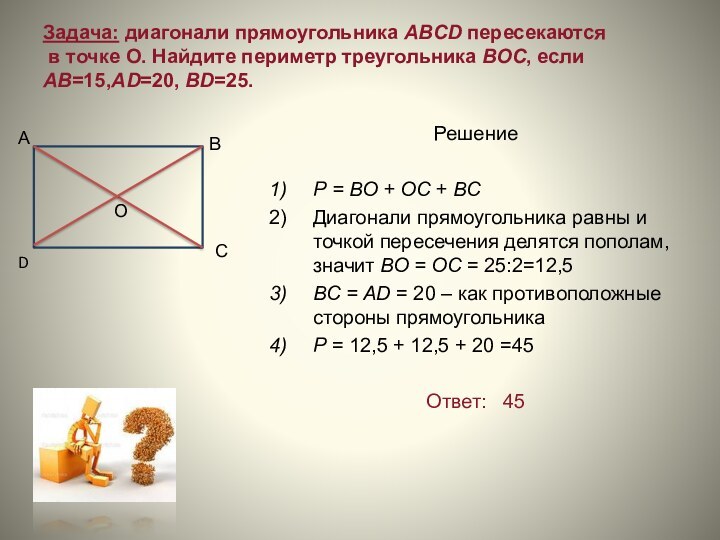
Слайд 14 Задача: диагонали прямоугольника ABCD пересекаются в точке О.

Найдите периметр треугольника ВОС, если АВ=15,AD=20, BD=25.
Решение

Р =

ВО + ОС + ВС
Диагонали прямоугольника равны и точкой пересечения делятся пополам, значит ВО = ОС = 25:2=12,5
ВС = АD = 20 – как противоположные стороны прямоугольника
Р = 12,5 + 12,5 + 20 =45

Ответ: 45

Слайд 15 Задача: один из углов ромба ABCD на 40

Задача: один из углов ромба ABCD на 40 ̊ больше другого.

̊ больше другого. Найдите углы треугольника ВОС, если О

- точка пересечения диагоналей.

Решение
В + С = 180۫º – как углы, прилежащие к одной стороне ромба
Составим уравнение х + х+ 40 = 180
2х = 140
х = 70
Значит, С = 70º
В = 70º+ 40º = 110º
3) Диагонали ромба перпендикулярны и являются биссектрисами его углов, поэтому в треугольнике ВОС
СОВ = 90º, СВО = 110º:2=55º,
ВСО = 70º:2=35º
Ответ: 90º; 55º; 35º

Слайд 16 Задача: в квадрате проведены диагонали. 1) Докажите, что при

Задача: в квадрате проведены диагонали. 1) Докажите, что при этом он

этом он разбивается на четыре равных равнобедренных треугольника. 2) Найдите

углы этих треугольников

Решение

Диагонали квадрата равны и точкой пересечения делятся пополам, поэтому BO=CO=DO=AO, а значит треугольники ВОС, АОВ, СОD, AOD – равнобедренные
Стороны квадрата равны, значит, Δ АОВ=
Δ ВОС= Δ COD= Δ АОD
3) Диагонали квадрата перпендикулярны и являются биссектрисами его углов, поэтому углы этих треугольников равны 90º; 45º; 45º

Ответ: 90º;45º; 45º

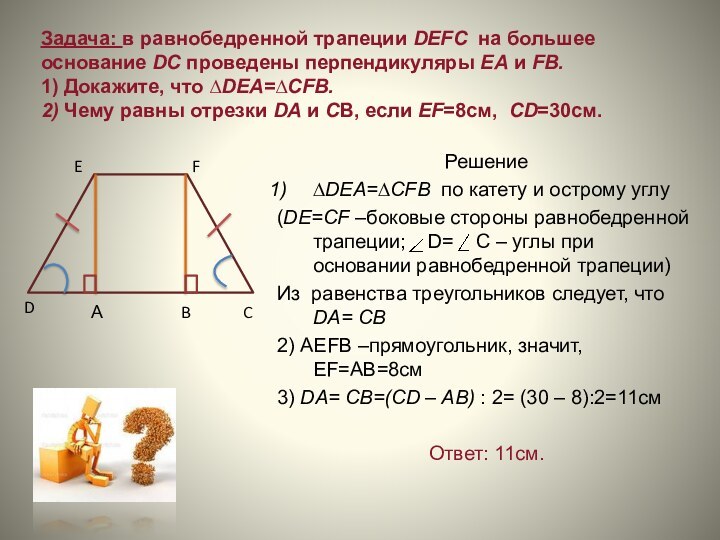
Слайд 17 Задача: в равнобедренной трапеции DEFC на большее основание

Задача: в равнобедренной трапеции DEFC на большее основание DC проведены перпендикуляры

DC проведены перпендикуляры ЕА и FB. 1) Докажите, что ∆DEA=∆CFB. 2)

Чему равны отрезки DA и CB, если EF=8cм, CD=30см.

Решение
∆DEA=∆CFB по катету и острому углу
(DE=CF –боковые стороны равнобедренной трапеции; D= C – углы при основании равнобедренной трапеции)
Из равенства треугольников следует, что DA= CB
2) АЕFB –прямоугольник, значит, ЕF=АВ=8см
3) DA= CB=(CD – AB) : 2= (30 – 8):2=11см

Ответ: 11см.

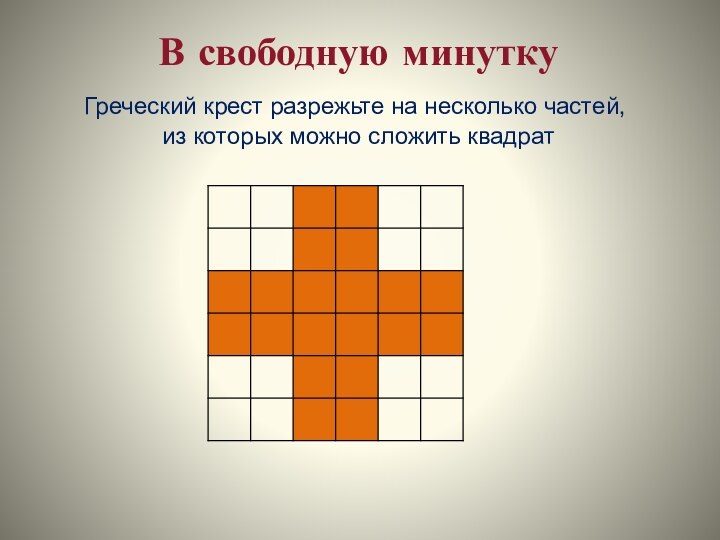
Слайд 18 В свободную минутку
Греческий крест разрежьте на несколько частей,

из которых можно сложить квадрат

Слайд 19 Комплекс упражнений «Танцуйте сидя»

Мы все вместе улыбнемся,

Комплекс упражнений «Танцуйте сидя» Мы все вместе улыбнемся, Подмигнем

Подмигнем слегка друг другу,
Вправо, влево повернемся
(повороты влево

- вправо)
И кивнем затем по кругу.
(наклоны влево - вправо)
Все идеи победили,
Вверх взметнулись наши руки.
(поднимают руки вверх – вниз)
Груз забот с себя стряхнули
И продолжим путь науки.
(встряхнули кистями рук)