- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Урок одной задачи
Содержание




Слайд 2
Задача С2
КИМ 5 июня 2013г.
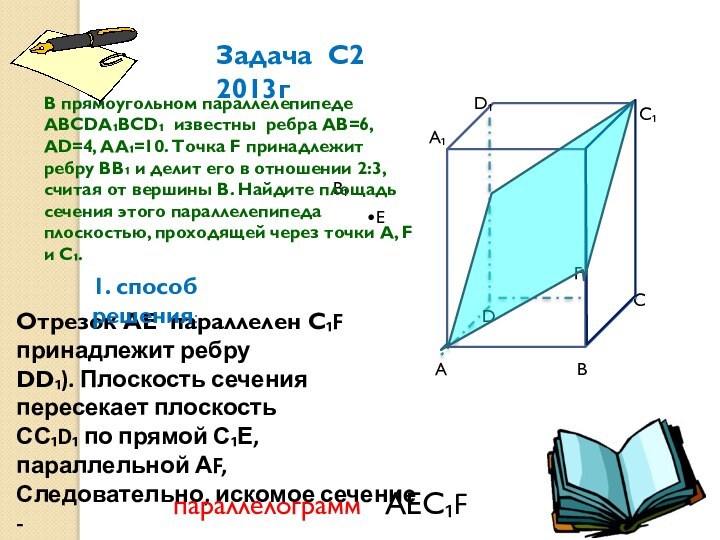
известны ребра АВ=6, АD=4, АА₁=10. Точка F принадлежит ребру ВВ₁ и делит его в отношении 2:3, считая от вершины В. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки А, F и С₁.
Слайд 3
В
Стандартная ошибка учащихся
F
F
А
В
С
С₁
D
В прямоугольном параллелепипеде АВСDА₁ВСD₁ известны
ребра АВ=6, АВ=4, АА₁=10. Точка F принадлежит ребру ВВ₁
и делит его в отношении 2:3, считая от вершины В. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки А, F и С₁.А₁
В₁
Слайд 4
А
А₁
В
С
С₁
D₁
D
В₁
F• •
•Е
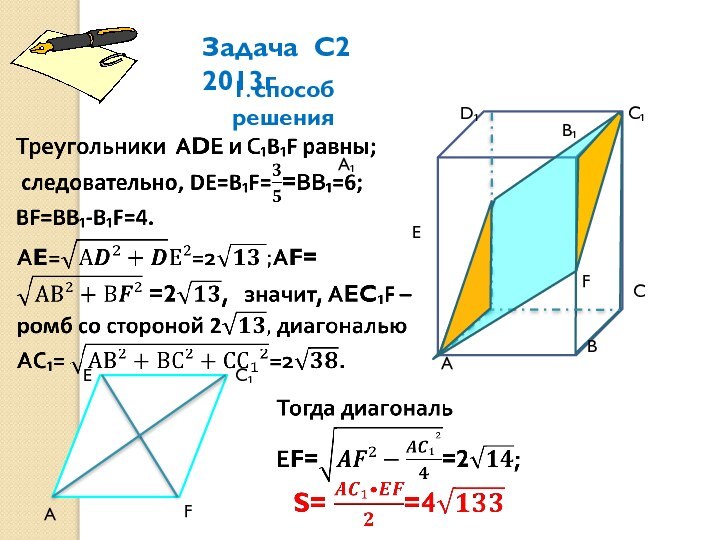
В прямоугольном параллелепипеде АВСDА₁ВСD₁ известны ребра АВ=6, АD=4, АА₁=10. Точка F принадлежит ребру ВВ₁ и делит его в отношении 2:3, считая от вершины В. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки А, F и С₁.
Отрезок АЕ параллелен С₁F принадлежит ребру
DD₁). Плоскость сечения пересекает плоскость
СС₁D₁ по прямой С₁Е, параллельной АF,
Следовательно, искомое сечение -
параллелограмм АЕС₁F
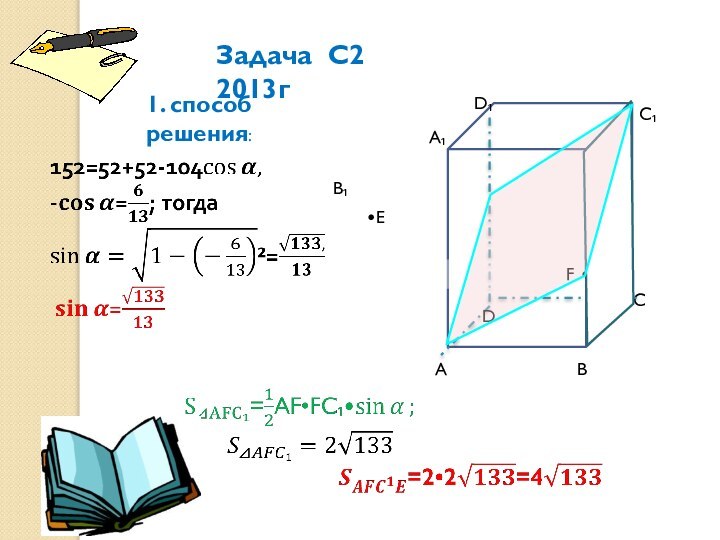
Задача С2 2013г
1. способ решения:
Слайд 6
А
А₁
В
С
С₁
D₁
D
В₁
F• •F
•Е
Задача С2 2013г
1. cпособ решения
Найду площадь сечения другим
способом:
Слайд 8
А
А₁
В
С
С₁
D₁
D
В₁
F•F
•Е
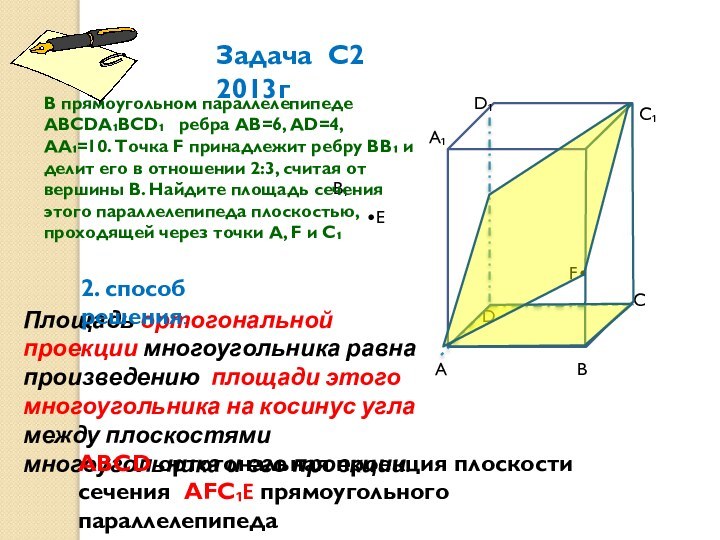
В прямоугольном параллелепипеде АВСDА₁ВСD₁ ребра АВ=6, АD=4, АА₁=10. Точка F принадлежит ребру ВВ₁ и делит его в отношении 2:3, считая от вершины В. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки А, F и С₁
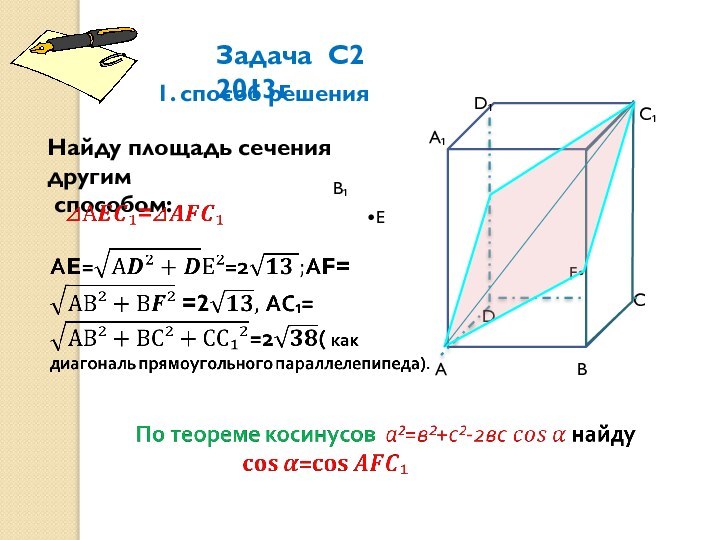
Площадь ортогональной проекции многоугольника равна произведению площади этого многоугольника на косинус угла между плоскостями многоугольника и его проекции.
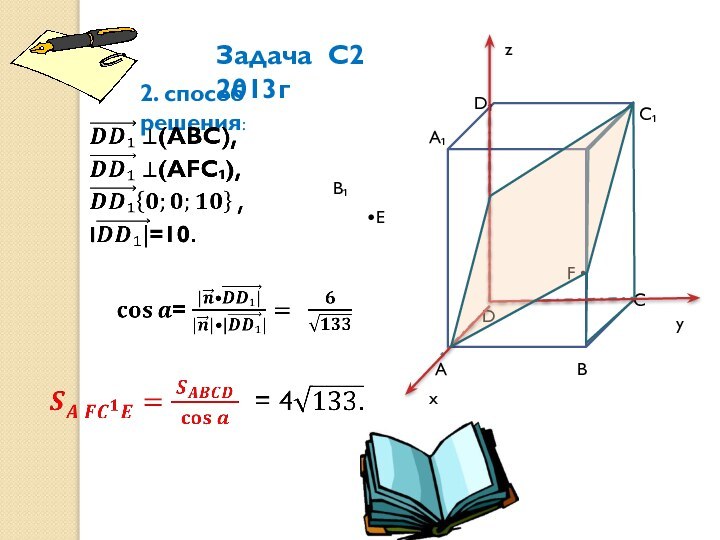
Задача С2 2013г
2. способ решения:
АВСD ортогональная проекция плоскости
cечения АFC₁E прямоугольного параллелепипеда
Слайд 9
А
А₁
В
С
С₁
D₁
D
В₁
F•F
•Е
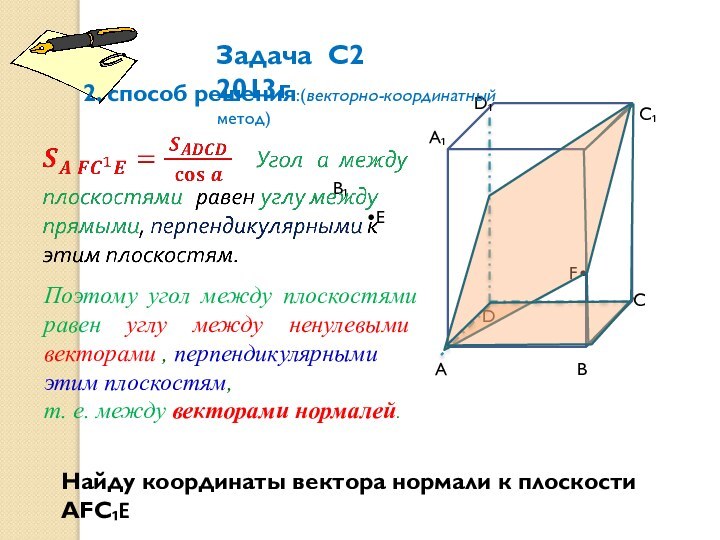
Задача С2 2013г
2. cпособ решения:(векторно-координатный
метод)
Поэтому угол между плоскостями равен углу между ненулевыми векторами , перпендикулярными
этим плоскостям,
т. е. между векторами нормалей.
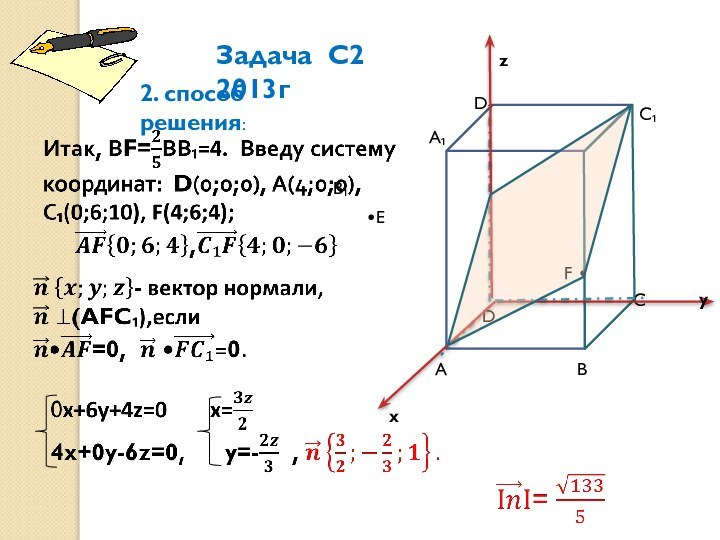
Найду координаты вектора нормали к плоскости АFC₁E