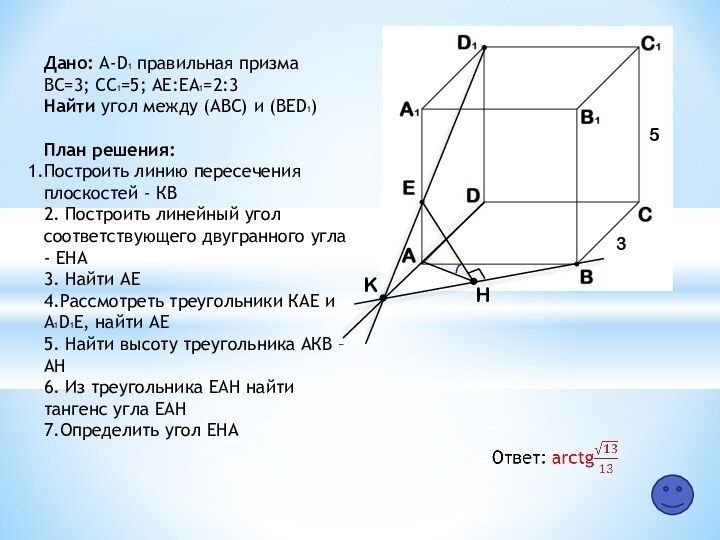
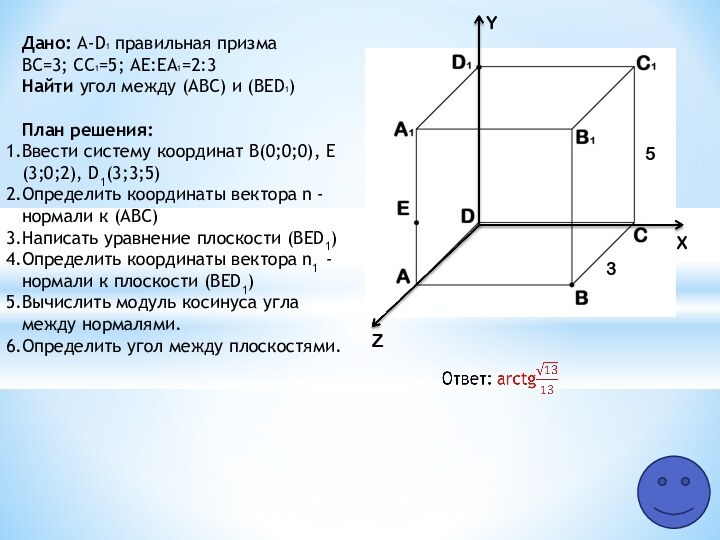
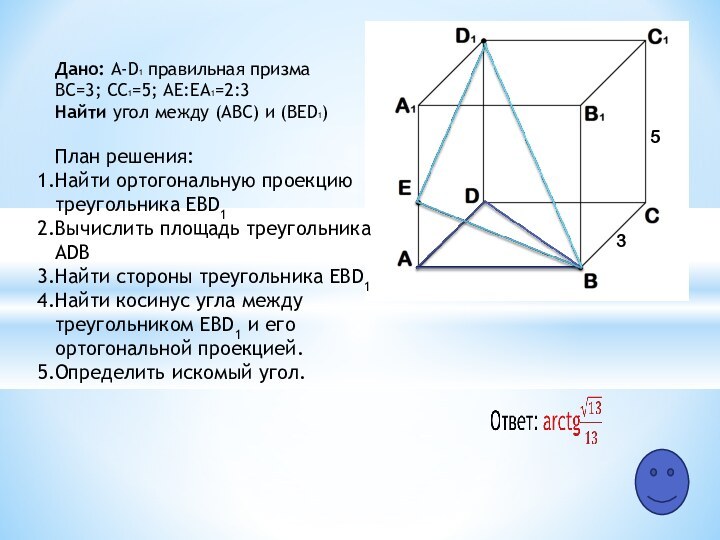
общий для всех способов решения справочный материал.
Данный прием наиболее
эффективен на уроках обобщения и систематизации знаний, т.к. позволят не только закрепить новый материал, но и ещё раз вспомнить пройденный.Урок решения одной задачи не следует проводить слишком часто, проведение таких уроков наиболее оправдано раз в четверть, или в полугодие, а так же во время итогового повторения, т.к. именно тогда можно подобрать комбинированную задачу, при решении которой применялся бы большой объем знаний.
Условия эффективности урока одной задачи