Презентация на тему Исследовательская работа по математике в 6 классе

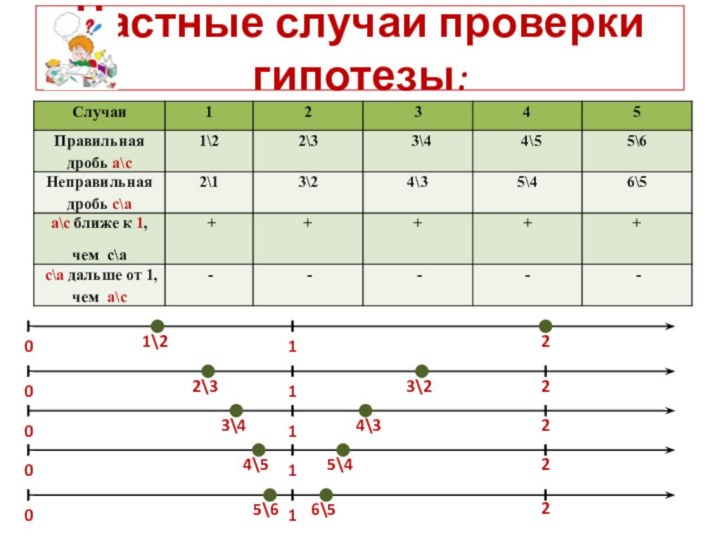
исследовательская работа № 1 - вывод
исследовательская

работа № 2 – вывод
Новая гипотеза
проверка новой гипотезы
доказательство гипотезы
Применение результатов полученного исследования при решении задач
Окончательные выводы

«Если к числителю

и знаменателю обыкновенных дробей прибавить одно и то же натуральное   число, то значение дроби не изменится».

дроби увеличивается и стремится к единице , но дробь

остается правильной.
 

дроби уменьшается и стремится к единице , но дробь

остается неправильной.
 

обратная к ней неправильная. Какая из этих дробей ближе

к единице?

2) Существуют ли дроби правильная и обратная к ней неправильная находящиеся на одинаковом расстоянии от 1?

гипотез
Докажем, что правильная дробь ближе к 1, чем

неправильная. Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца. Пусть А(1), В( а\с), С(с\а )
1– а\с = с\с – а\с = (с – а)\с;
с\а – 1 = с\а – а\а = (с-а)\а ;
с-а\с < с-а\а, так как из двух дробей с одинаковыми числителями меньше та, у которой знаменатель больше (с > а).

0

1

а\с

с\а

А

В

С

Доказательство выдвинутых гипотез

Докажем, что не существует такой

правильной дроби и обратной к ней, которые находятся на одинаковом расстоянии от 1.

(с– а)\с ≠ (с – а)\а,
так как с ≠ а

1
Не приводя к общему знаменателю, сравни

дроби:
52\53 и 53\54
Задача № 2
Два одинаковых сосуда наполнены жидкостью. Из первого сосуда взяли 7\16 имеющейся там жидкости, а из второго сосуда 8\17 имеющейся там жидкости. В каком сосуде осталось больше жидкости?
Задача № 3
Найдите дробь, меньше 5\4 .
Задача № 4
Найдите дробь, больше 4\5 .