Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по математике на тему Касательная к окружности

Содержание

Взаимное расположение прямой и окружности.ОАВСDRОR – радиусСD – диаметрAB - хорда
19.03.14 Классная работа Касательная к окружности. П69,№634,636 Взаимное расположение прямой и окружности.ОАВСDRОR – радиусСD – диаметрAB - хорда Дано:Окружность с центром в точке О радиуса rПрямая, которая не проходит через Возможны три случая:1) d Возможны три случая:2) d=rЕсли расстояние от центра окружности до прямой равно радиусу Возможны три случая:3) d>rЕсли расстояние от центра окружности до прямой больше радиуса Касательная к окружностиОпределение: Прямая, имеющая с окружностью только одну общую точку, называется Сколько общих точек могут иметь прямая и окружность? d < rd = Выясните взаимное расположение прямой и окружности, если:r = 15 см, d = Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, Свойство касательных, проходящих через одну точку:▼ По свойству касательной ∆АВО, ∆АСО–прямоугольные∆АВО=∆АСО–по
Слайды презентации

Слайд 2

Слайд 3

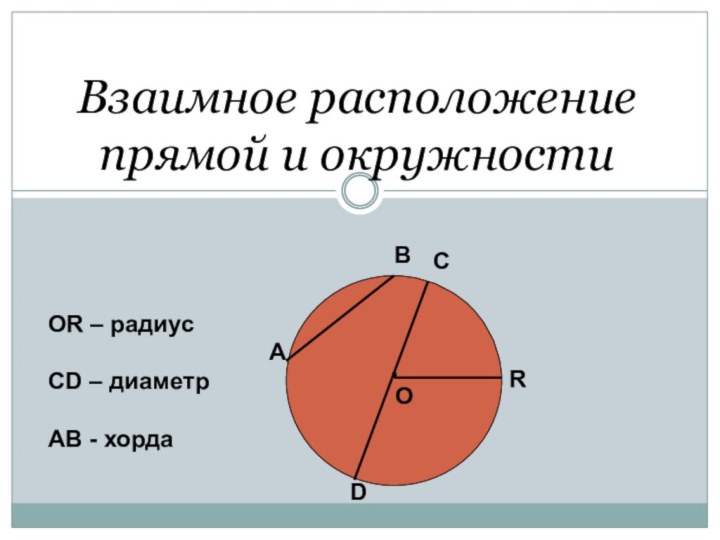
Слайд 4 Взаимное расположение прямой и окружности

.
О
А
В
С
D
R
ОR – радиус

СD –

Взаимное расположение прямой и окружности.ОАВСDRОR – радиусСD – диаметрAB - хорда

диаметр

AB - хорда

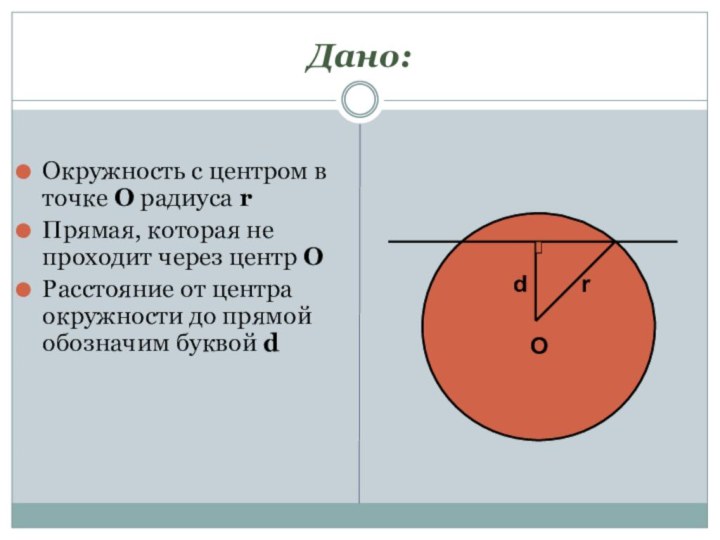
Слайд 5 Дано:

Окружность с центром в точке О радиуса r
Прямая,

Дано:Окружность с центром в точке О радиуса rПрямая, которая не проходит

которая не проходит через центр О
Расстояние от центра окружности

до прямой обозначим буквой d


O

r

d


Слайд 6 Возможны три случая:
1) d

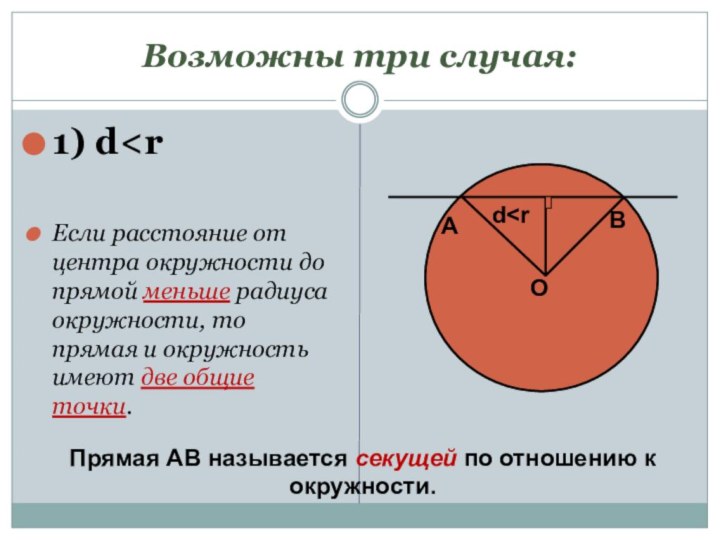
Возможны три случая:1) d

до прямой меньше радиуса окружности, то прямая и окружность

имеют две общие точки.


O

d


А

В

Прямая АВ называется секущей по отношению к окружности.

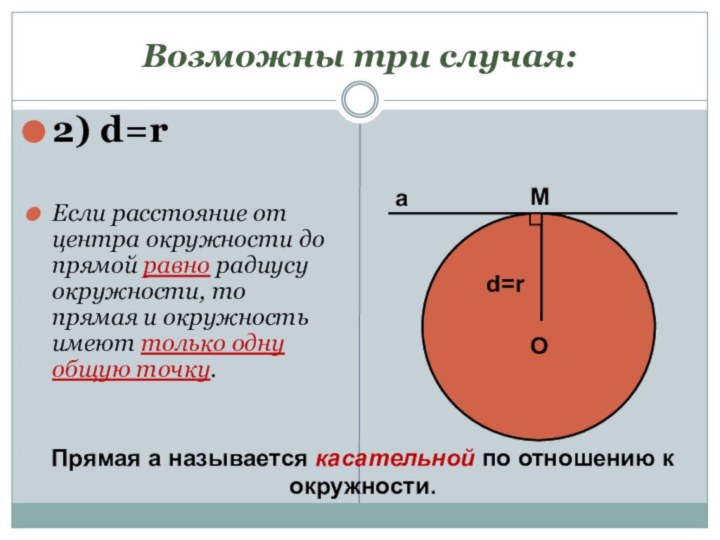
Слайд 7 Возможны три случая:
2) d=r

Если расстояние от центра окружности

Возможны три случая:2) d=rЕсли расстояние от центра окружности до прямой равно

до прямой равно радиусу окружности, то прямая и окружность

имеют только одну общую точку.


O

d=r


M

а

Прямая а называется касательной по отношению к окружности.

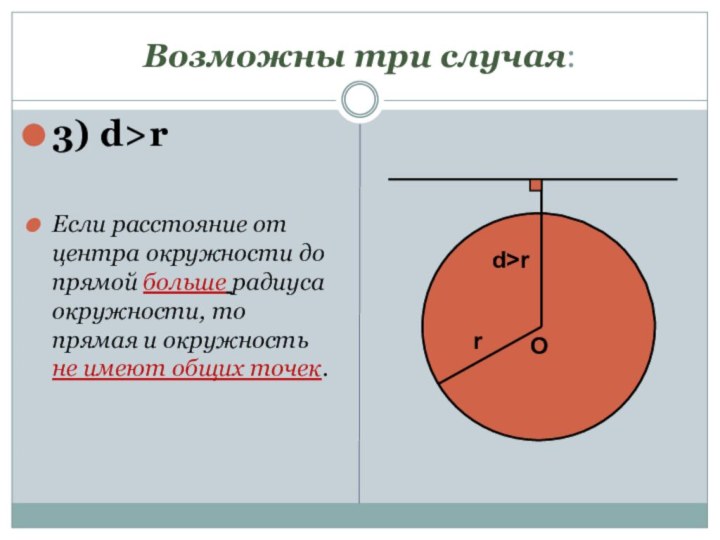
Слайд 8 Возможны три случая:
3) d>r

Если расстояние от центра окружности

Возможны три случая:3) d>rЕсли расстояние от центра окружности до прямой больше

до прямой больше радиуса окружности, то прямая и окружность

не имеют общих точек.


O

d>r


r

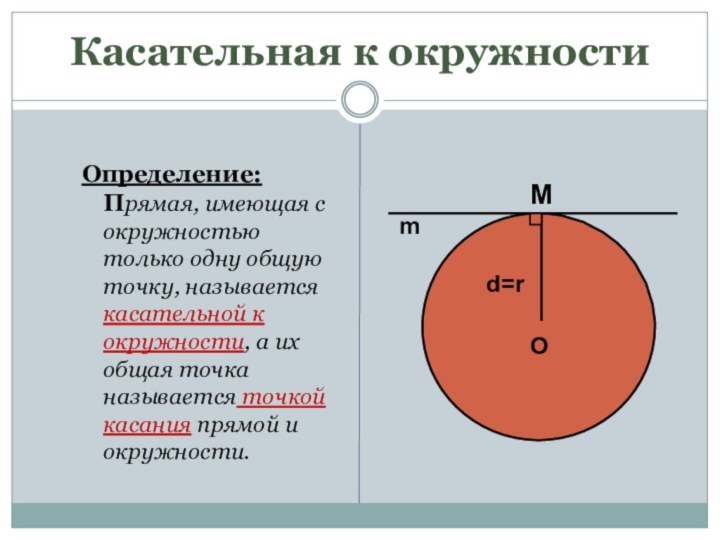
Слайд 9 Касательная к окружности
Определение: Прямая, имеющая с окружностью только

Касательная к окружностиОпределение: Прямая, имеющая с окружностью только одну общую точку,

одну общую точку, называется касательной к окружности, а их

общая точка называется точкой касания прямой и окружности.


O

d=r


M

m

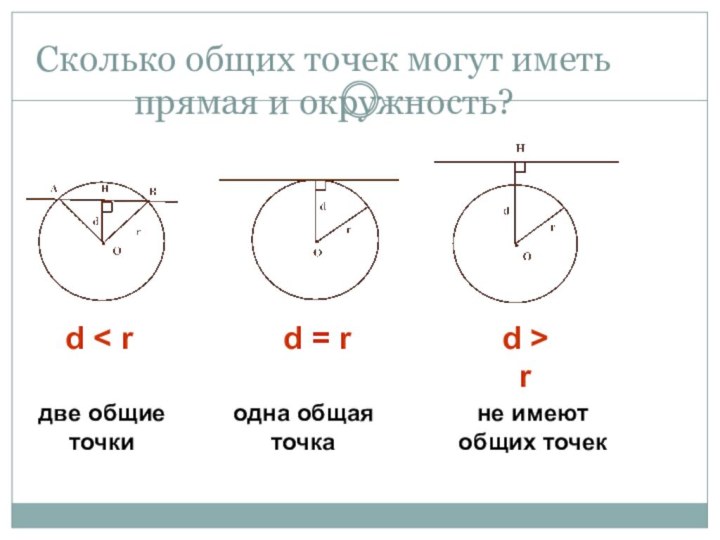
Слайд 10 Сколько общих точек могут иметь прямая и окружность?

Сколько общих точек могут иметь прямая и окружность? d < rd


d < r
d = r

d > r
две общие точки
одна

общая точка

не имеют общих точек

Слайд 11 Выясните взаимное расположение прямой и окружности, если:
r =

Выясните взаимное расположение прямой и окружности, если:r = 15 см, d

15 см, d = 11см
r = 6 см, d

= 5,2 см
r = 3,2 м, d = 4,7 м
r = 7 см, d = 0,5 дм
r = 4 см, d = 40 мм

прямая – секущая
прямая – секущая
общих точек нет
прямая – секущая
прямая - касательная

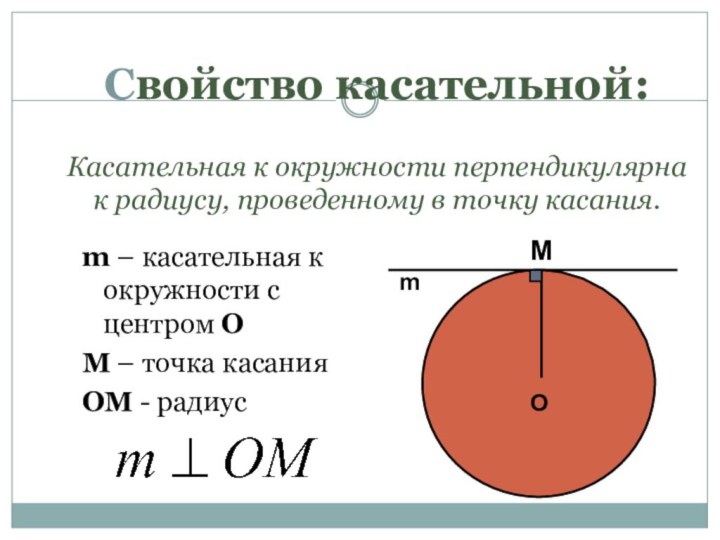
Слайд 12 Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному

Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку

в точку касания.
m – касательная к окружности с центром

О
М – точка касания
OM - радиус




O


M

m

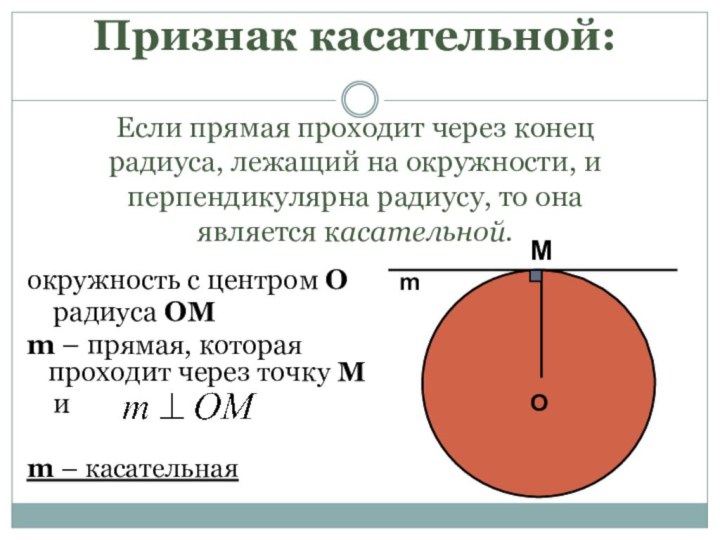
Слайд 13 Признак касательной: Если прямая проходит через конец радиуса, лежащий

Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности,

на окружности, и перпендикулярна радиусу, то она является касательной.
окружность

с центром О
радиуса OM
m – прямая, которая проходит через точку М
и

m – касательная





O


M

m

Слайд 14


Слайд 15 Свойство касательных, проходящих через одну точку:
▼ По свойству

Свойство касательных, проходящих через одну точку:▼ По свойству касательной ∆АВО, ∆АСО–прямоугольные∆АВО=∆АСО–по

касательной

∆АВО, ∆АСО–прямоугольные
∆АВО=∆АСО–по гипотенузе и катету:
ОА – общая,
ОВ=ОС

– радиусы

АВ=АС и
▲


О

В

С

А

1

2

3

4


Отрезки касательных к
окружности, проведенные
из одной точки, равны и
составляют равные углы
с прямой, проходящей через
эту точку и центр окружности.

Prezented.Ru

Слайд 16


Слайд 17


  • Имя файла: prezentatsiya-po-matematike-na-temu-kasatelnaya-k-okruzhnosti.pptx
  • Количество просмотров: 131
  • Количество скачиваний: 0
- Предыдущая Презентация к уроку Кислоты по химии
Следующая - Презентация. Семья в современном обществе.

Похожие презентации

Моделирование ценовой политики Моделирование ценовой политики 97
Числовые выражения. Задачи на проценты. 7 класс Числовые выражения. Задачи на проценты. 7 класс 130
Аттестационная работа. Составление терминологического словаря с греческими и латинскими корнями по математике и физике Аттестационная работа. Составление терминологического словаря с греческими и латинскими корнями по математике и физике 93
Презентация внеурочного занятия Математика и здоровье (5 класс) Презентация внеурочного занятия Математика и здоровье (5 класс) 166
Презентация Путь к домику Незнайки презентация к уроку по математике (средняя группа) Презентация Путь к домику Незнайки презентация к уроку по математике (средняя группа) 102
Конспект интегрированного занятия с использованием интерактивной доски план-конспект занятия по математике (старшая группа) Конспект интегрированного занятия с использованием интерактивной доски план-конспект занятия по математике (старшая группа) 103
Геометрический конструктор Геометрический конструктор 126
Принцип Принцип 97
Математические методы в психологии Математические методы в психологии 118
Презентация: Умножение числа на произведение презентация к уроку по математике (4 класс) Презентация: Умножение числа на произведение презентация к уроку по математике (4 класс) 48
Презентация к уроку математики на тему Вероятность события Презентация к уроку математики на тему Вероятность события 123
Презентации по математике учащихся Презентации по математике учащихся 98
Презентация к уроку по теме Деление многозначных чисел Презентация к уроку по теме Деление многозначных чисел 81
Урок математики во 2 классе по теме Прямоугольник план-конспект урока по математике (2 класс) Урок математики во 2 классе по теме Прямоугольник план-конспект урока по математике (2 класс) 122
Задания по теме Деление Задания по теме Деление 109
Вычитание Вычитание 128
Презентация к уроку математики Презентация к уроку математики 143
Презентация Узоры и орнаменты на посуде. презентация к уроку по математике (старшая группа) Презентация Узоры и орнаменты на посуде. презентация к уроку по математике (старшая группа) 129
Начала Евклида Начала Евклида 123
Бенефис дробей Бенефис дробей 111
Единицы времени 4 класс Единицы времени 4 класс 110
Интерактивная игра по математике Интерактивная игра по математике 163
122
Из истории мер длины Из истории мер длины 47
Геометрические преобразования графиков функций Геометрические преобразования графиков функций 94
ustnyy schyot 4 klass ustnyy schyot 4 klass 131
Числа 1-6 Числа 1-6 125
Порядок действий в вычислениях Порядок действий в вычислениях 145
Презентация Треугольники презентация к уроку по математике (3 класс) Презентация Треугольники презентация к уроку по математике (3 класс) 153
Презентация по математике Геометрические фигуры презентация по математике Презентация по математике Геометрические фигуры презентация по математике 109