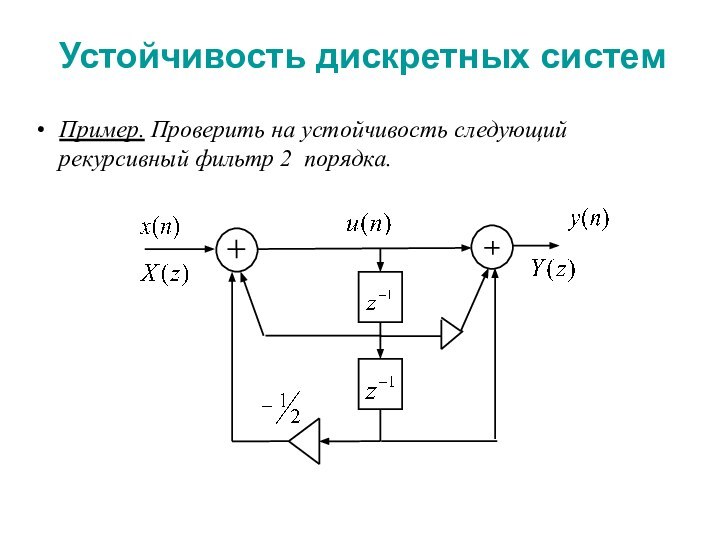
(13.1) не выполняется, то есть
.Рассмотрим ограниченную последовательность, заданную значениями:
Так как выходные отсчеты сигнала равны свертке входных отсчетов и значений импульсной характеристики дискретной системы, то есть
то при отклик системы равен: