ПОНЯТИЕ СИСТЕМЫ
5.2. ТЕХНОЛОГИЯ ПОСТРОЕНИЯ РАСЧЁТНОЙ СХЕМЫ СИСТЕМЫ (ВАГОНА)
5.3. СТРУКТУРНЫЕ
ФУНКЦИИ СИСТЕМ5.4. СИСТЕМЫ С ПРИВОДИМОЙ И НЕПРИВОДИМОЙ СТРУКТУРОЙ
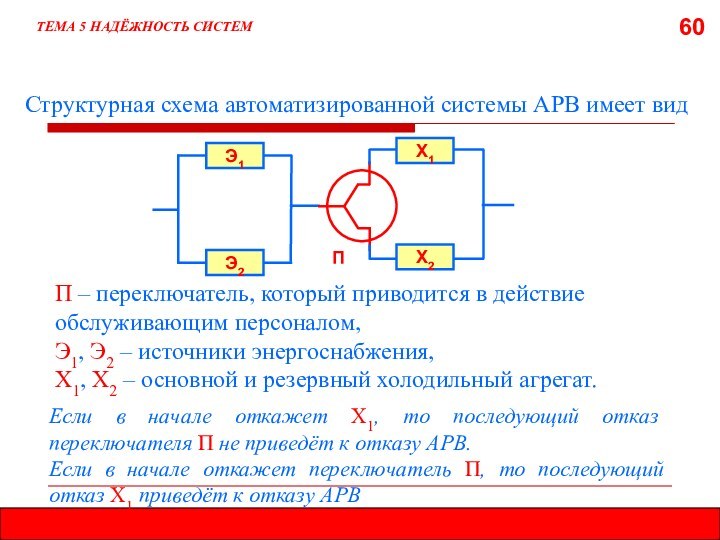
5.5. МЕТОД СТРУКТУРНЫХ СХЕМ
5.6. МЕТОД ПЕРЕБОРА СОСТОЯНИЙ
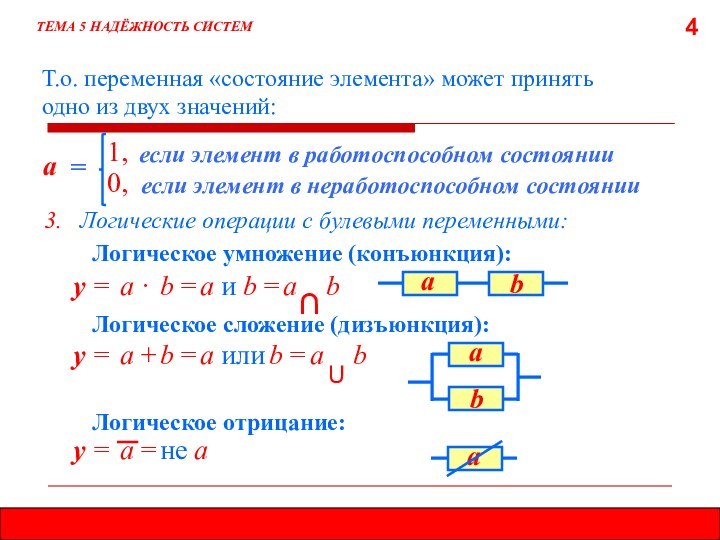
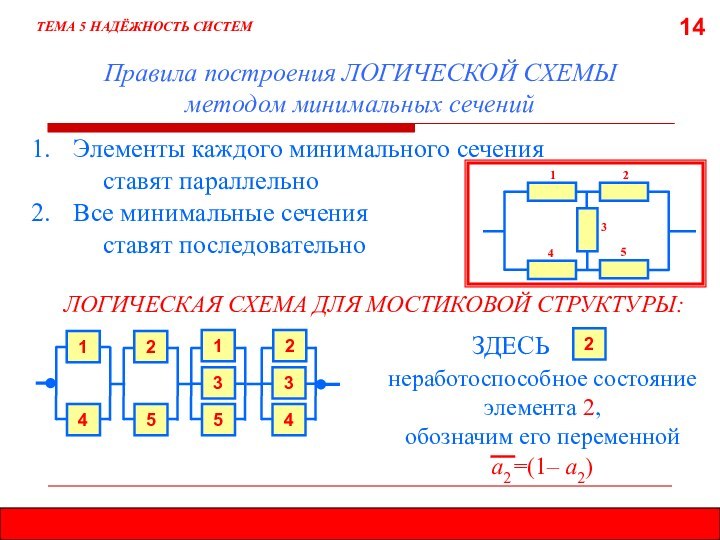
5.7. МЕТОД ЛОГИЧЕСКИХ СХЕМ
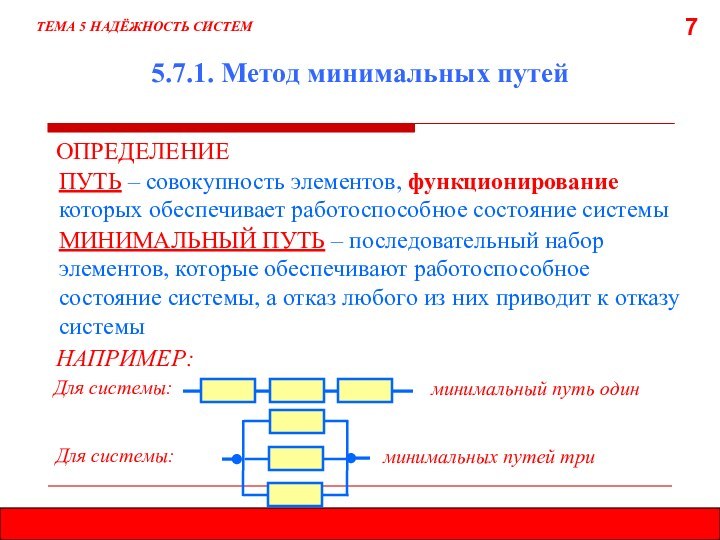
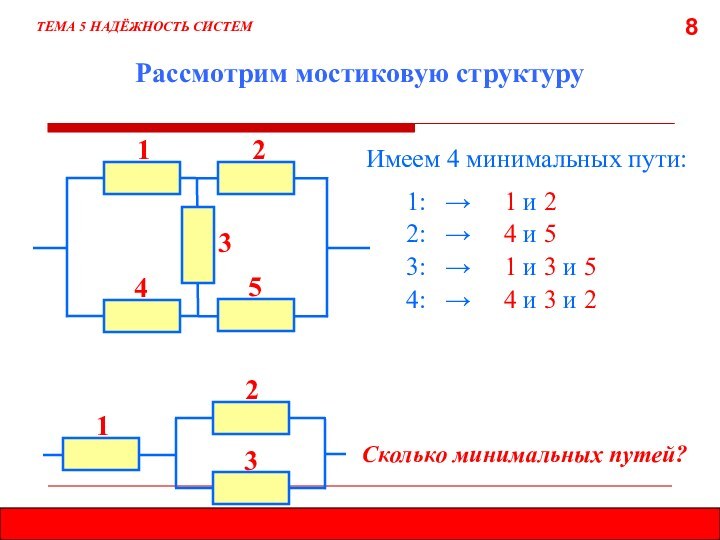
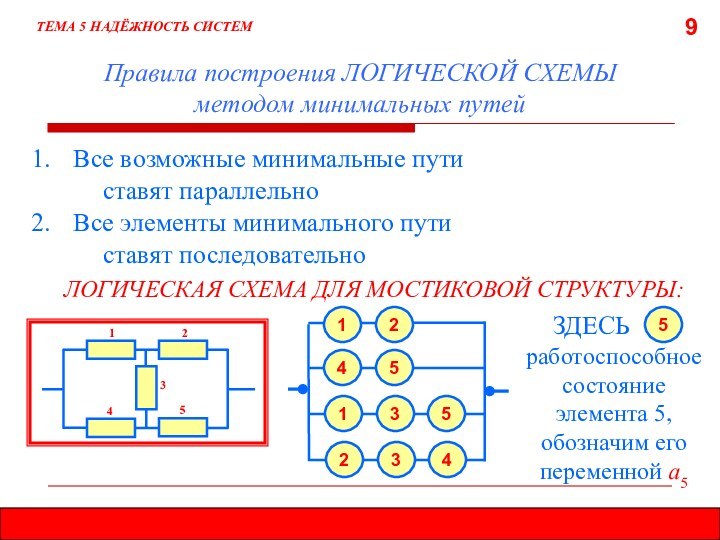
5.7.1. МЕТОД МИНИМАЛЬНЫХ ПУТЕЙ
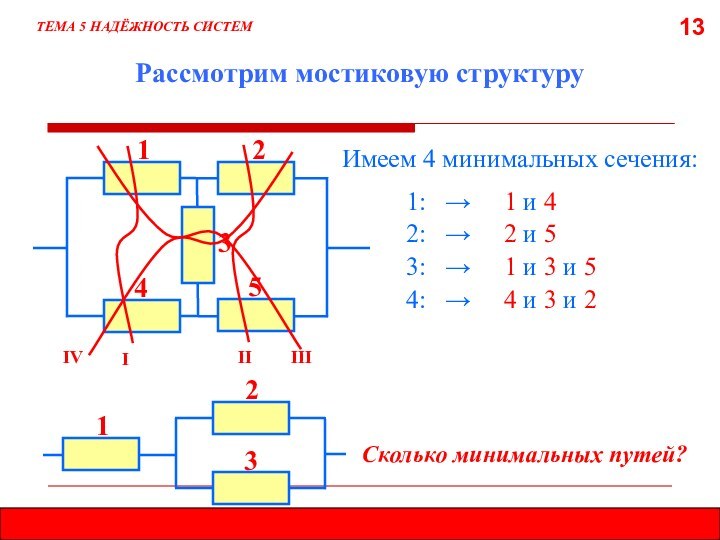
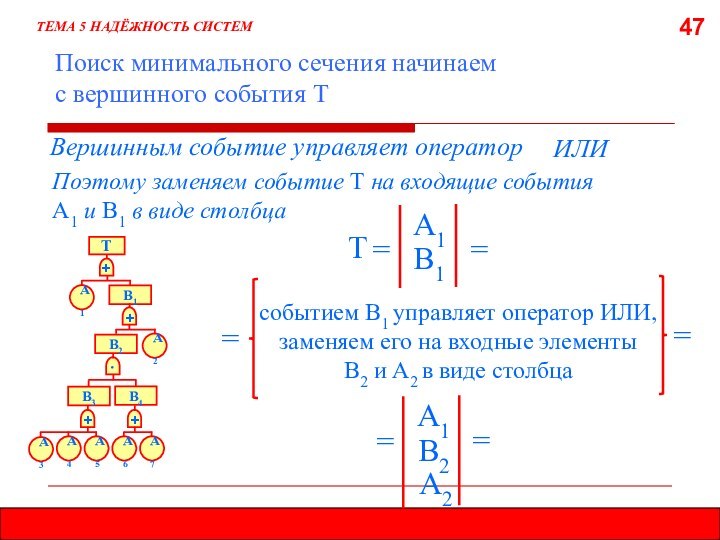
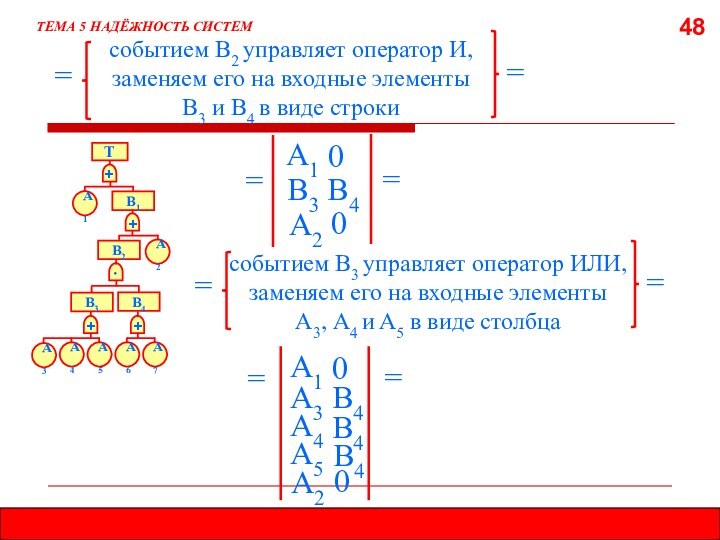
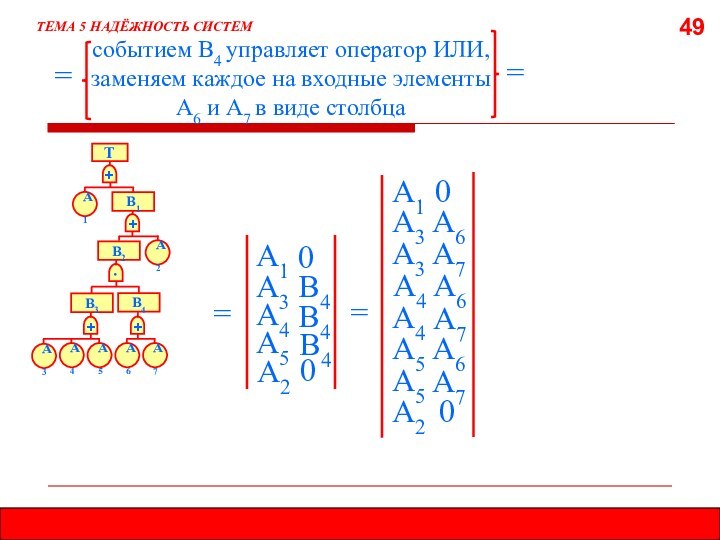
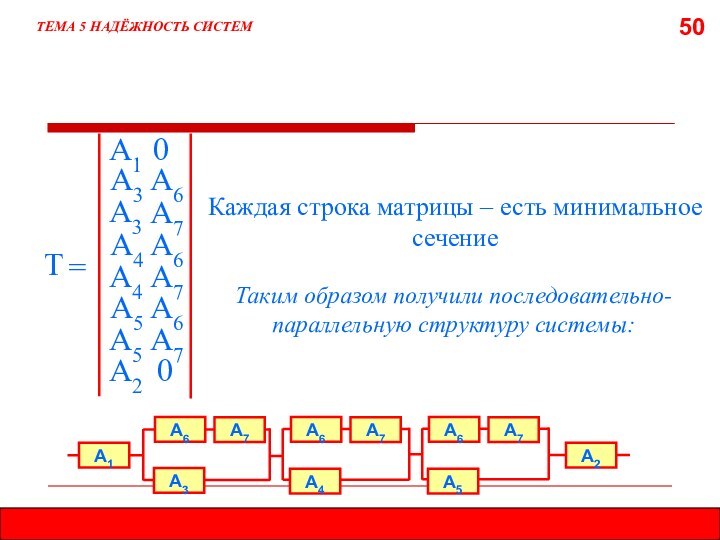
5.7.2. МЕТОД МИНИМАЛЬНЫХ СЕЧЕНИЙ
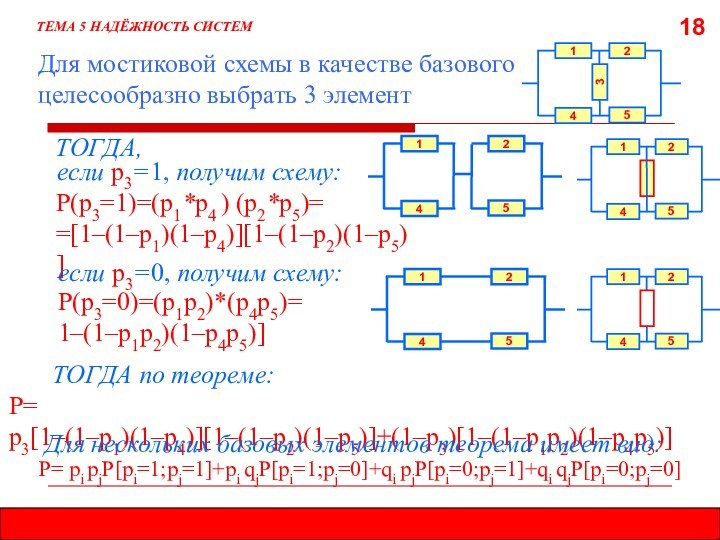
5.7.3. МЕТОД РАЗЛОЖЕНИЯ ПО БАЗОВОМУ ЭЛЕМЕНТУ
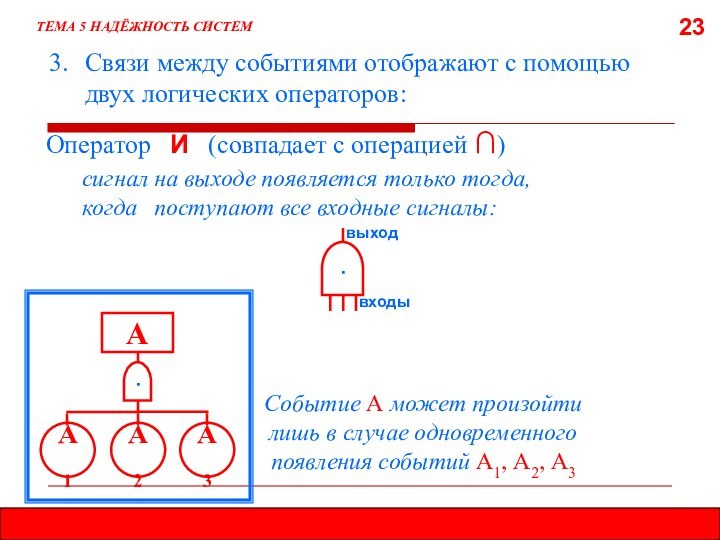
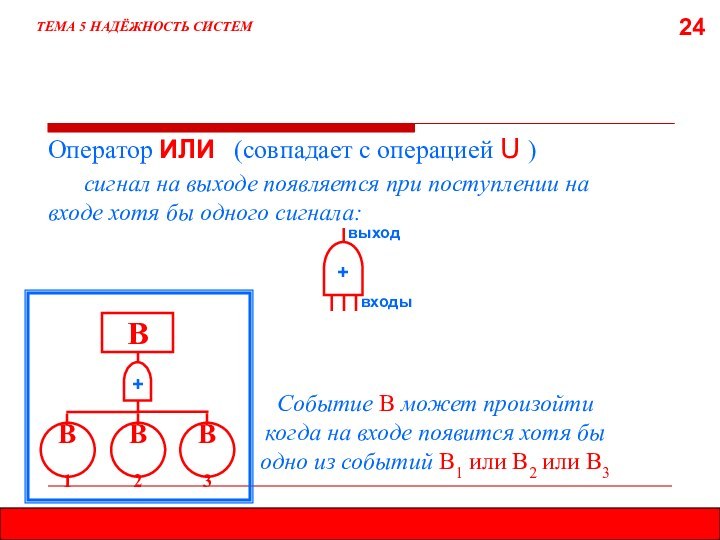
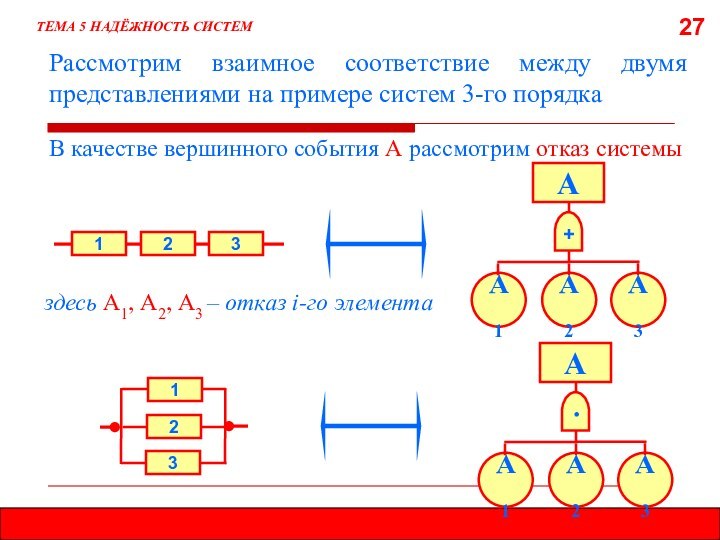
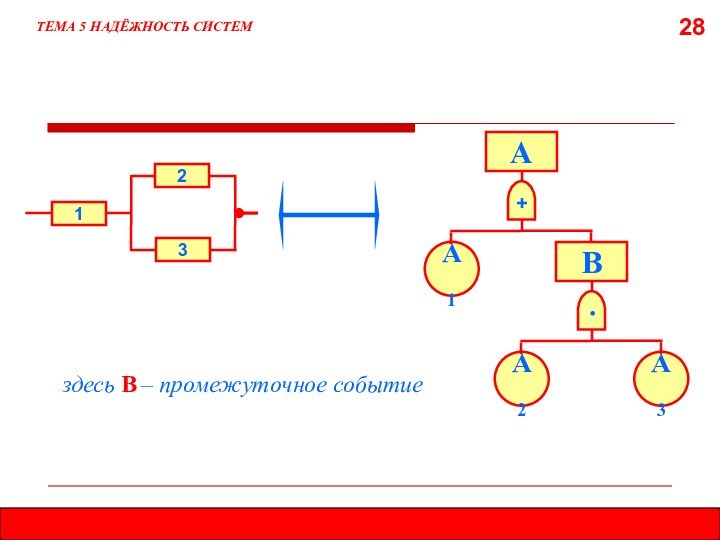
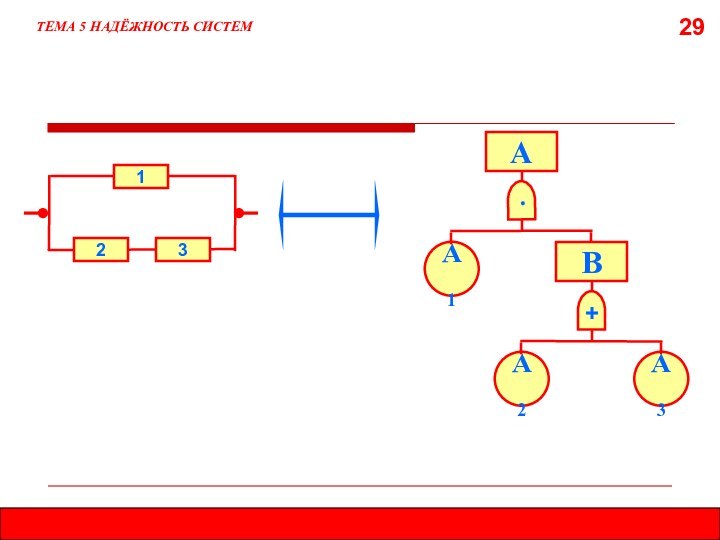
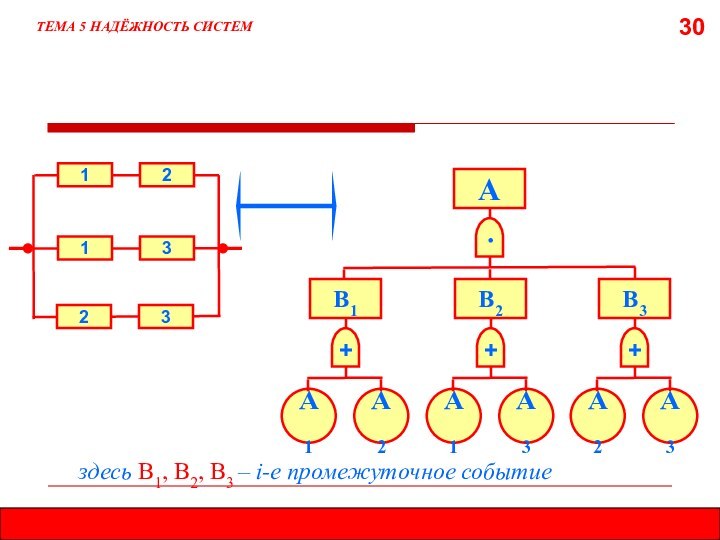
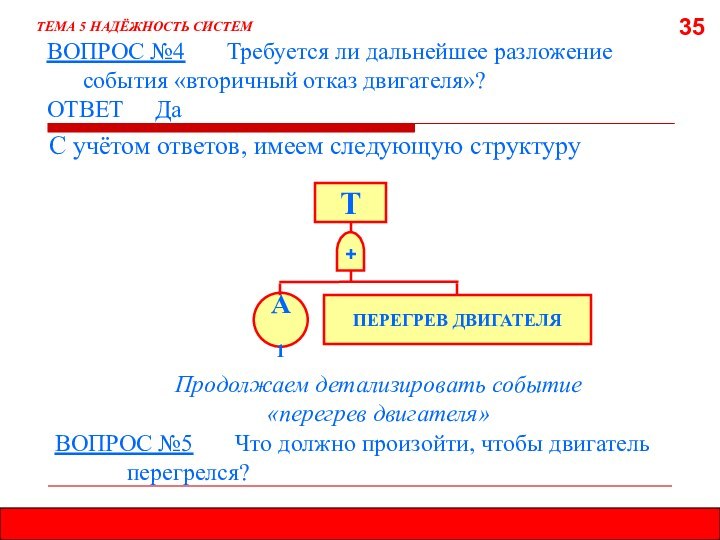
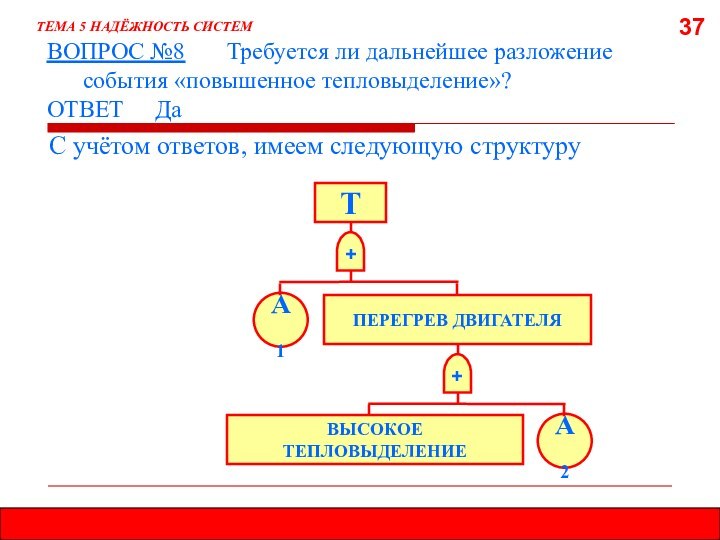
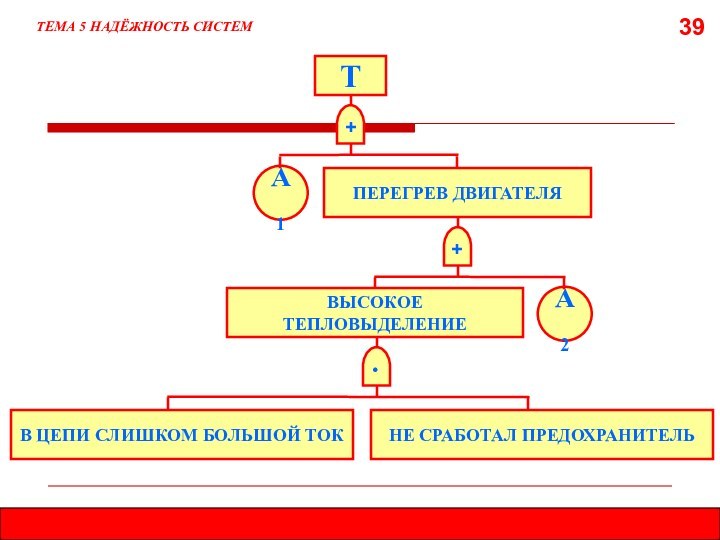
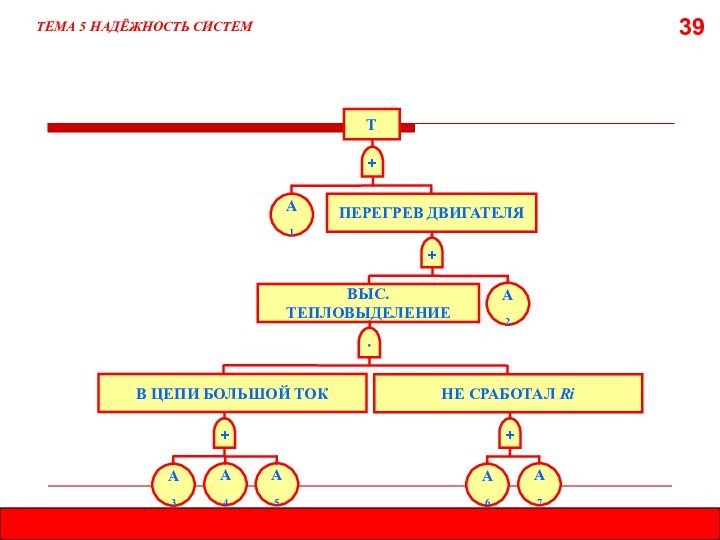
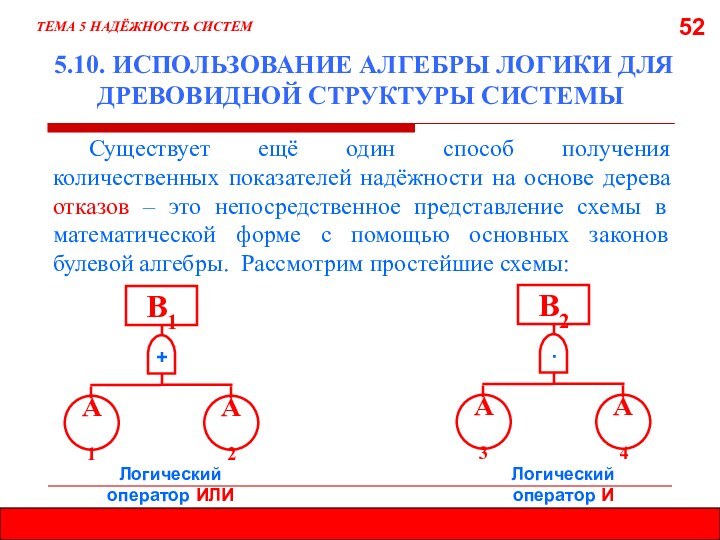
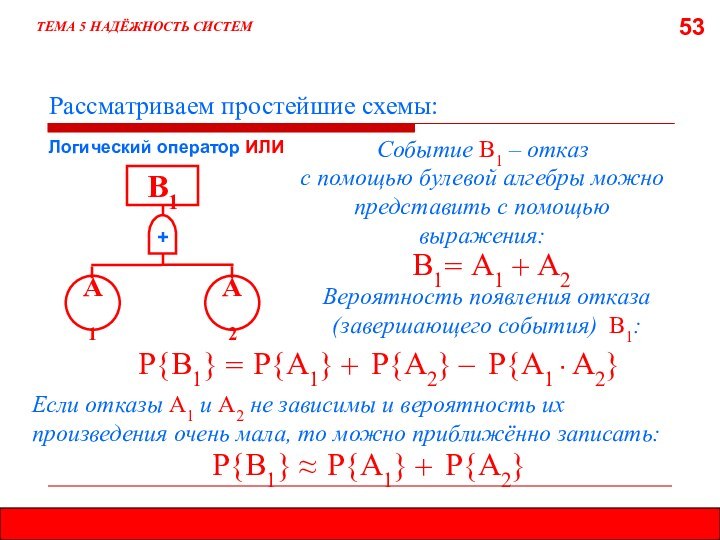
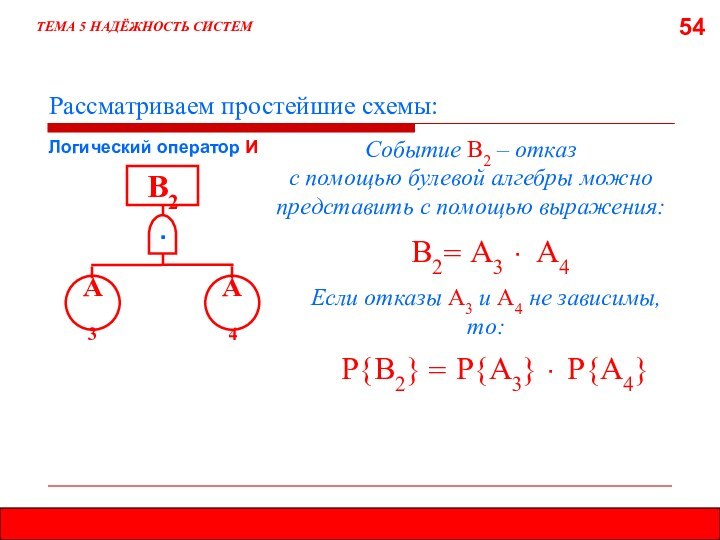
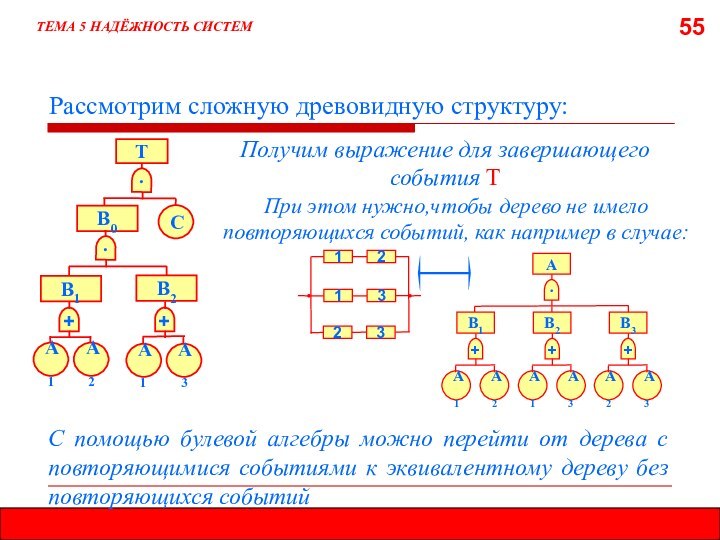
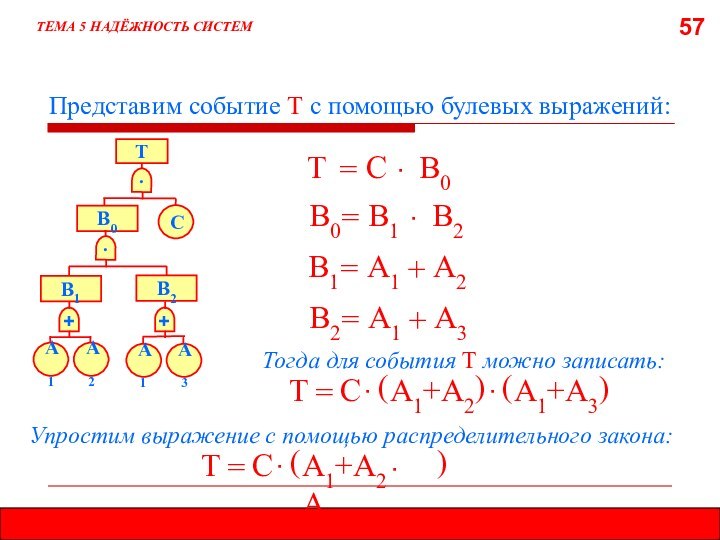
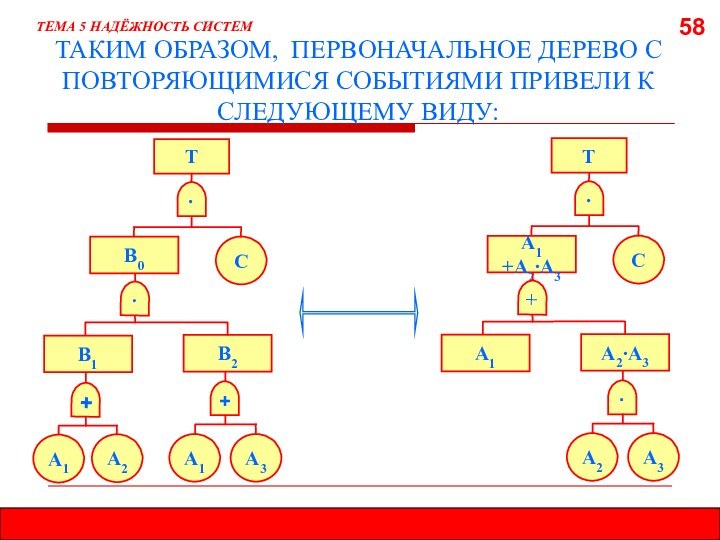
5.8. МЕТОД ДЕРЕВА ОТКАЗОВ (ДЕРЕВА СОБЫТИЙ)
5.9. НАДЁЖНОСТЬ РЕМОНТИРУЕМЫХ СИСТЕМ
5.10. НАДЁЖНОСТЬ СИСТЕМЫ СО МНОГИМИ СОСТОЯНИЯМИ