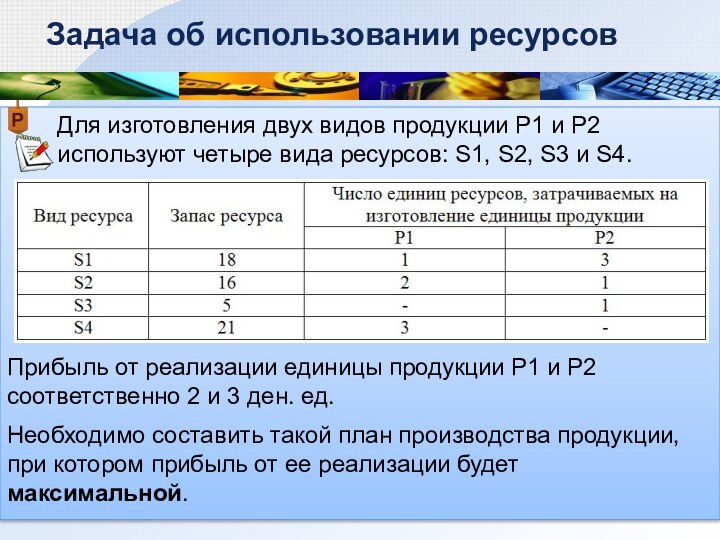
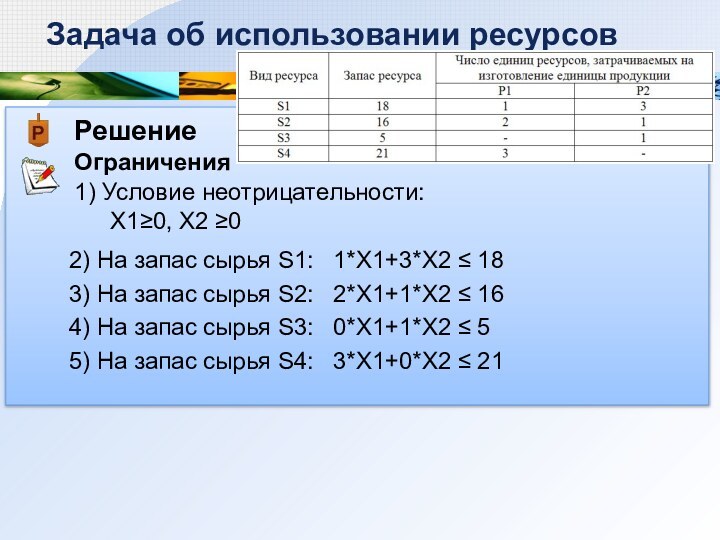
используют четыре вида ресурсов: S1, S2, S3 и S4.
Задача
об использовании ресурсовПрибыль от реализации единицы продукции Р1 и Р2 соответственно 2 и 3 ден. ед.
Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.