- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Вариационные ряды распределения
Содержание
- 2. Статистические ряды распределения. Определение. Виды. Примеры.Атрибутивный ряд распределения.Вариационный ряд распределения.Графическое изображение рядов распределения.Полигон.Гистограмма.КумулятаОгиваСтатистические таблицы.Содержание
- 3. Статистический ряд распределения – это упорядоченное распределение
- 4. Атрибутивными — называют ряды распределения, построенные по
- 5. Вариационными рядами называют ряды распределения, построенные по
- 6. В зависимости от характера вариации признака различают
- 7. Пример дискретного вариационного ряда: Таблица 2 -
- 8. При расчете средней арифметической в интервальном ряду
- 9. Наглядно ряды распределения представляются при помощи графических изображений.Ряды распределения изображаются в виде:ПолигонаГистограммыКумулятыОгивыГрафическое изображение рядов распределения
- 10. При построении полигона на горизонтальной оси (ось
- 11. Условие: Приводятся данные о распределении 25 работников
- 13. Если значения признака выражены в виде интервалов,
- 14. На рис. 6.2. изображена гистограмма распределения населения России в 1997 г. по возрастным группам.
- 15. Условие: Приводится распределение 30 работников фирмы по
- 17. Распределение признака в вариационном ряду по накопленным
- 18. Рассчитаем накопленные частоты:Наколенная частота первого интервала рассчитывается
- 19. При построении кумуляты накопленная частота (частость) соответствующего интервала присваивается его верхней границе:
- 20. Огива строится аналогично кумуляте с той лишь
- 22. Статистическая таблица – это особый способ краткой
- 23. Условие: Приведены данные о размерах вкладов 20
- 24. Скачать презентацию
- 25. Похожие презентации
Статистические ряды распределения. Определение. Виды. Примеры.Атрибутивный ряд распределения.Вариационный ряд распределения.Графическое изображение рядов распределения.Полигон.Гистограмма.КумулятаОгиваСтатистические таблицы.Содержание
















Слайд 2
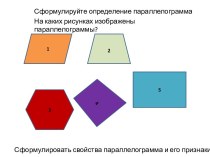
Статистические ряды распределения. Определение. Виды. Примеры.
Атрибутивный ряд распределения.
Вариационный
ряд распределения.
Слайд 3 Статистический ряд распределения – это упорядоченное распределение единиц
совокупности на группы по определённому варьирующему признаку.
В зависимости
от признака, положенного в основу образования ряда распределения, различают атрибутивные и вариационные ряды распределения.Ряд распределения — представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку.
Слайд 4 Атрибутивными — называют ряды распределения, построенные по качественными
признакам. Ряд распределения принято оформлять в виде таблиц.
Таблица 1
- Распределение видов юридической помощи, оказанной адвокатами гражданам одного из регионов РФ.Слайд 5 Вариационными рядами называют ряды распределения, построенные по количественному
признаку. Любой вариационный ряд состоит из двух элементов: вариантов
и частот.Вариантами считаются отдельные значения признака, которые он принимает в вариационном ряду.
Частоты – это численности отдельных вариантов или каждой группы вариационного ряда, т.е. это числа, показывающие, как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот определяет численность всей совокупности, её объём. Обозначаются ( )
Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100 %.
Обозначаются ( )
Слайд 6 В зависимости от характера вариации признака различают дискретные
и интервальные вариационные ряды.
Вариационный ряд называется дискретным, если
любые его варианты отличаются на постоянную величину, и интервальным, если варианты могут отличаться один от другого на сколь угодно малую величину. Интервалы в ряду могут быть как равными, так и неравными. Это зависит от характера статистических данных и задач исследования.Виды вариационный рядов
Слайд 7
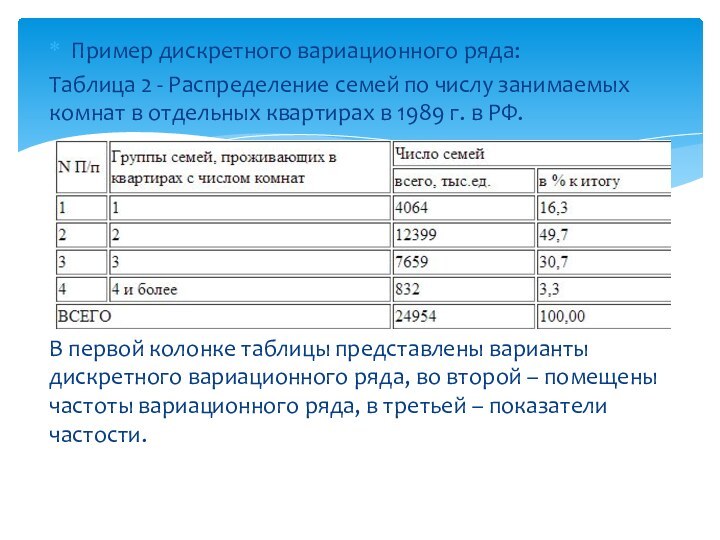
Пример дискретного вариационного ряда:
Таблица 2 - Распределение
семей по числу занимаемых комнат в отдельных квартирах в
1989 г. в РФ.В первой колонке таблицы представлены варианты дискретного вариационного ряда, во второй – помещены частоты вариационного ряда, в третьей – показатели частости.
Слайд 8 При расчете средней арифметической в интервальном ряду за
значение варианты принимается середина интервала. Середина интервала вычисляется как
среднее арифметическое его границ.Медиана (Ме) Срединное значение варьирующего признака в упорядоченном (ранжированном) ряду. Применяется в случаях, когда совокупность статистических данных неоднородна (асимметрична), поскольку Ме менее чувствительна к средним значениям ряда, чем средняя арифметическая.
Мода (Мо) Наиболее часто встречающаяся в ряду варианта. В интервальном вариационном ряду определяется модальный интервал. Мо используется для характеристики среднего уровня в неоднородных совокупностях, как и медиана.
Размах вариации (R) - разность максимального и минимального значений периода в вариационном ряду.
R=xmax-xmin
Зависит от случайных колебаний выборки, т.е. для вычисления R используются лишь крайние значения варианты.
Дисперсия - представляет собой среднюю арифметическую квадратов отклонений всех вариант от их средней арифметической.
Слайд 9
Наглядно ряды распределения представляются при помощи графических изображений.
Ряды
распределения изображаются в виде:
Полигона
Гистограммы
Кумуляты
Огивы
Графическое изображение рядов распределения
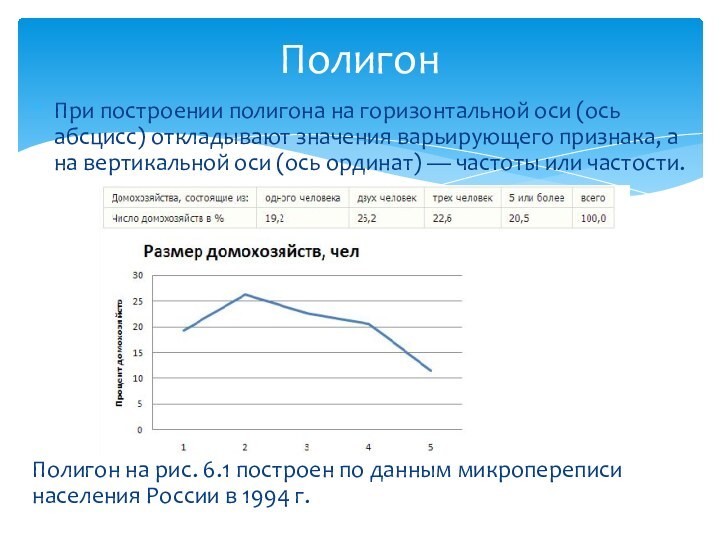
Слайд 10 При построении полигона на горизонтальной оси (ось абсцисс)
откладывают значения варьирующего признака, а на вертикальной оси (ось
ординат) — частоты или частости.Полигон на рис. 6.1 построен по данным микропереписи населения России в 1994 г.
Полигон
Слайд 11 Условие: Приводятся данные о распределении 25 работников одного
из предприятий по тарифным разрядам: 4; 2; 4; 6;
5; 6; 4; 1; 3; 1; 2; 5; 2; 6; 3; 1; 2; 3; 4; 5; 4; 6; 2; 3; 4Задача: Построить дискретный вариационный ряд и изобразить его графически в виде полигона распределения.
Решение:В данном примере вариантами является тарифный разряд работника. Для определения частот необходимо рассчитать число работников, имеющих соответствующий тарифный разряд.
Для построения полигона распределения (рис 1) по оси абсцисс (X) откладываем количественные значения варьирующего признака — варианты, а по оси ординат — частоты или частости.
Слайд 13 Если значения признака выражены в виде интервалов, то
такой ряд называется интервальным.
Интервальные ряды распределения изображают графически в
виде гистограммы.Гистограмма – график, на котором ряд изображен в виде смежных друг с другом столбиков. Для построения гистограммы по оси абсцисс указывают значения границ интервалов и на их основании строят прямоугольники, высота которых пропорциональна частотам (или частостям).
Гистограмма
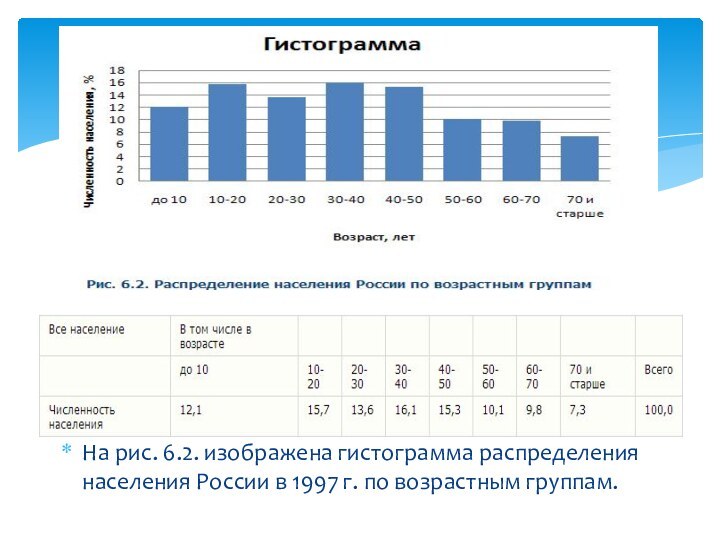
Слайд 14 На рис. 6.2. изображена гистограмма распределения населения России
в 1997 г. по возрастным группам.
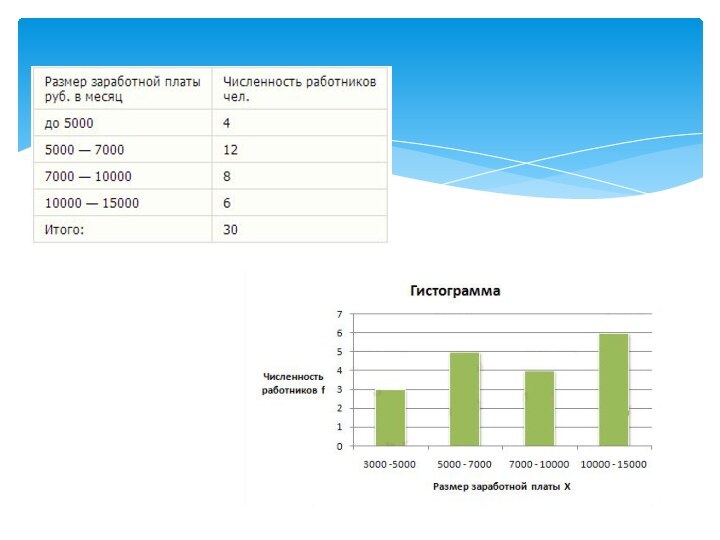
Слайд 15 Условие: Приводится распределение 30 работников фирмы по размеру
месячной заработной платы
Задача: Изобразить интервальный вариационный ряд графически в
виде гистограммы и кумуляты.Решение:
Неизвестная граница открытого (первого) интервала определяется по величине второго интервала: 7000 — 5000 = 2000 руб. С той же величиной находим нижнюю границу первого интервала: 5000 — 2000 = 3000 руб.
Для построения гистограммы в прямоугольной системе координат по оси абсцисс откладываем отрезки, величины которых соответствуют интервалам варицонного ряда.
Эти отрезки служат нижним основанием, а соответствующая частота (частость) — высотой образуемых прямоугольников.
3. Построим гистограмму:
Слайд 17 Распределение признака в вариационном ряду по накопленным частотам
(частостям) изображается с помощью кумуляты.
Кумулята или кумулятивная кривая в
отличие от полигона строится по накопленным частотам или частостям. При этом на оси абсцисс помещают значения признака, а на оси ординат — накопленные частоты или частости .Для построения кумуляты необходимо рассчитать накопленные частоты (частости). Они определяются путем последовательного суммирования частот (частостей) предшествующих интервалов и обозначаются S. Накопленные частоты показывают, сколько единиц совокупности имеют значение признака не больше, чем рассматриваемое.
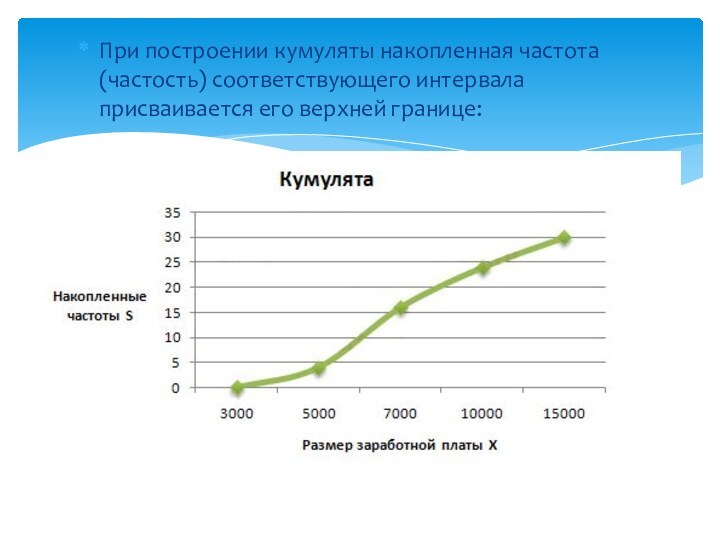
Кумулята
Слайд 18
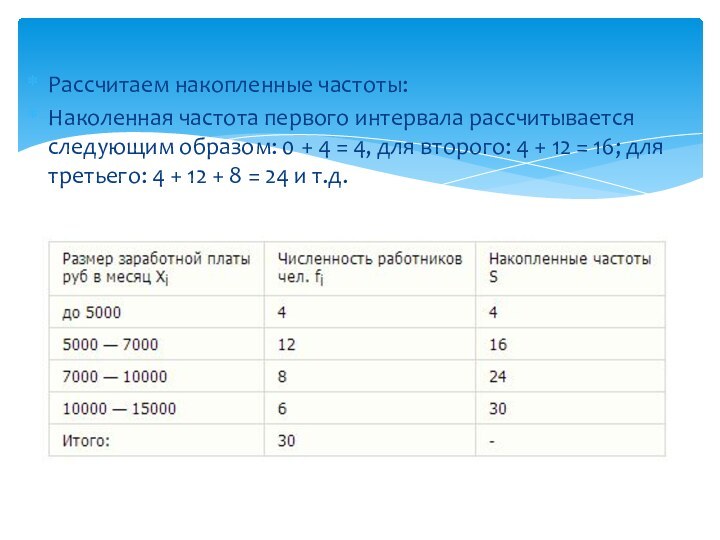
Рассчитаем накопленные частоты:
Наколенная частота первого интервала рассчитывается следующим
образом: 0 + 4 = 4, для второго: 4
+ 12 = 16; для третьего: 4 + 12 + 8 = 24 и т.д.Слайд 19 При построении кумуляты накопленная частота (частость) соответствующего интервала
присваивается его верхней границе:
Слайд 20 Огива строится аналогично кумуляте с той лишь разницей,
что накопленные частоты помещают на оси абсцисс, а значения
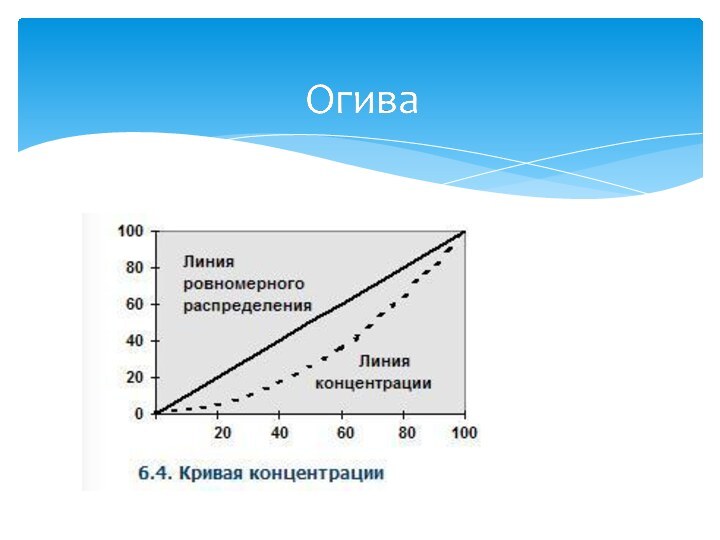
признака — на оси ординат.Разновидностью кумуляты является кривая концентрации или график Лоренца. Для построения кривой концентрации на обе оси прямоугольной системы координат наносится масштабная шкала в процентах от 0 до 100. При этом на оси абсцисс указывают накопленные частости, а на оси ординат — накопленные значения доли (в процентах) по объему признака.
Равномерному распределению признака соответствует на графике диагональ квадрата (рис. 6.4). При неравномерном распределении график представляет собой вогнутую кривую в зависимости от уровня концентрации признака.
Огива
Слайд 22 Статистическая таблица – это особый способ краткой и
наглядной записи сведений об изучаемых общественных явлениях. Статистическая таблица
позволяет охватить материалы статистической сводки в целом, она также является системой мыслей об исследуемом объекте, излагаемых цифрами на основе определенного порядка в расположении систематизированной информации.Статистические таблицы
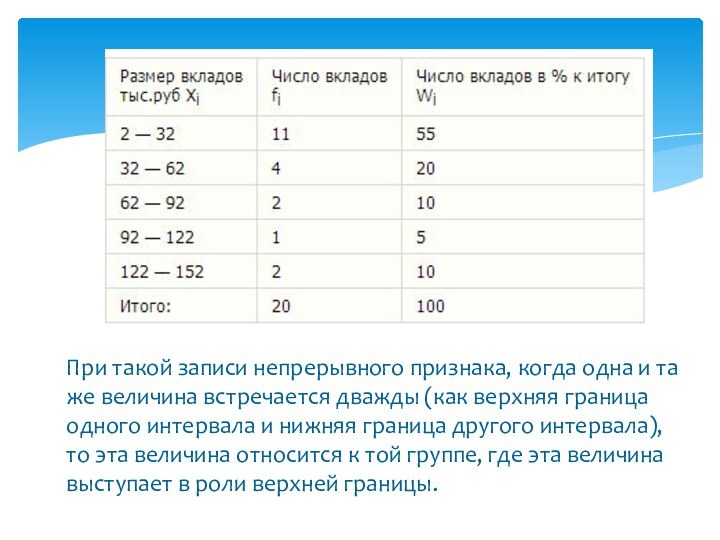
Слайд 23 Условие: Приведены данные о размерах вкладов 20 физических
лиц в одном банке (тыс.руб) 60; 25; 12; 10;
68; 35; 2; 17; 51; 9; 3; 130; 24; 85; 100; 152; 6; 18; 7; 42.Задача: Построить интервальный вариационный ряд с равными интервалами.
Решение:
Исходная совокупность состоит из 20 единиц (N = 20).
По формуле Стерджесса определим необходимое количество используемых групп: n=1+3,322*lg20=5
Вычислим величину равного интервала: i=(152 — 2) /5 = 30 тыс.руб
Расчленим исходную совокупность на 5 групп с величиной интервала в 30 тыс.руб.
Результаты группировки представим в таблице: