- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Погрешности измерений
Содержание
- 2. Погрешности измеренийИнструментальные погрешности:Инструментальные погрешности, являющиеся следствием износа,
- 3. Погрешности измеренийСпособы исключения и учета систематических погрешностей.
- 4. Погрешности измеренийУстранение источников погрешностей до начала измерений.
- 5. Погрешности измеренийУстранение систематических погрешностей Одним из наиболее
- 6. Погрешности измеренийСпособ компенсации погрешности по знаку. Измерение
- 7. Погрешности измеренийСлучайные погрешности Математические модели случайной погрешности.Прислучайных
- 8. Погрешности измеренийСреднее арифметическое ряда измерений: Это наиболее вероятный результат измерения
- 9. Погрешности измеренийГауссовский закон распределения(в практике радиоизмерений наиболее распространён)p(ΔX) - плотность вероятности случайной погрешности
- 10. Погрешности измеренийФункция Гаусса Графически изображается колоколообразной кривой,
- 11. Погрешности измеренийВероятность появления погрешности в пределах между
- 12. Погрешности измеренийИз таблиц, приведенных в математических справочниках,
- 13. Погрешности измеренийПредставленные ф-лы выведены из расчета, что
- 14. Погрешности измеренийСредее квадратическое отклонение среднего арифметического
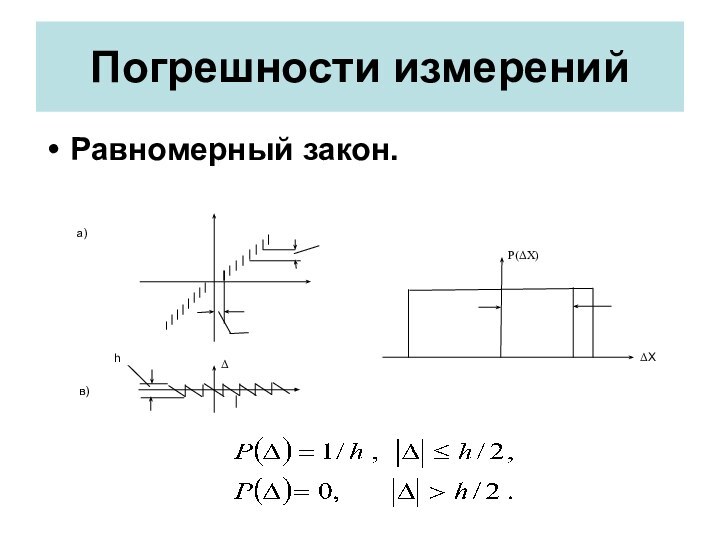
- 15. Погрешности измеренийРавномерный закон.
- 16. Погрешности измеренийДисперсия случайной погрешности при равномерном законеСреднее квадратическое отклонение
- 17. Погрешности измеренийТреугольный закон распределения погрешностей. Треугольный закон является композицией двух равномерных законов с одинаковой дисперсией.
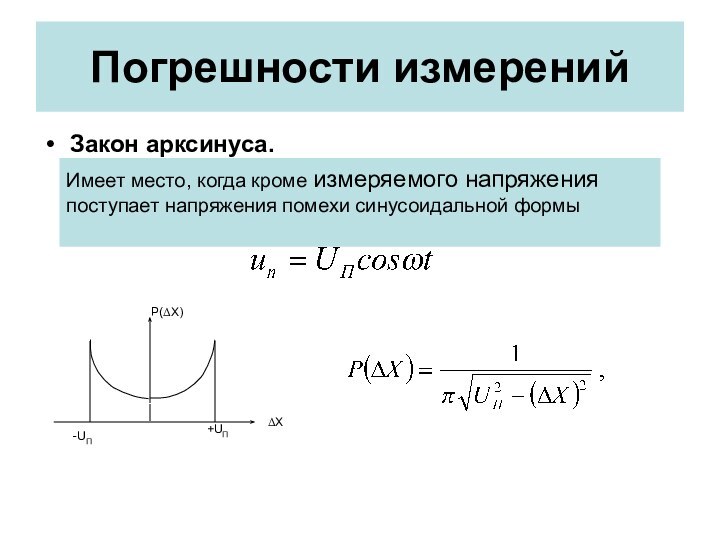
- 18. Погрешности измеренийЗакон арксинуса.Имеет место, когда кроме измеряемого напряжения поступает напряжения помехи синусоидальной формы
- 19. Скачать презентацию
- 20. Похожие презентации
Погрешности измеренийИнструментальные погрешности:Инструментальные погрешности, являющиеся следствием износа, старения или неисправности СИ.Погрешности, возникающие вследствие неправильной установки СИ, их неправильным взаимным расположением, влиянием внешних воздействий.















Слайд 2
Погрешности измерений
Инструментальные погрешности:
Инструментальные погрешности, являющиеся следствием износа, старения
или неисправности СИ.
неправильным взаимным расположением, влиянием внешних воздействий.
Слайд 3
Погрешности измерений
Способы исключения и учета систематических погрешностей.
Четыре
основные группы:
устранение источников погрешностей до начала измерений;
исключение погрешностей в
процессе измерения способами замещения, компенсации погрешности по знаку, противопоставления, симметричных наблюдений;внесение поправок в результат измерения;
оценка границ не исключенных систематических погрешностей.
Слайд 4
Погрешности измерений
Устранение источников погрешностей до начала измерений.
Под
устранением источника погрешностей понимается как его непосредственное удаление (например,
удаление источника тепла), так и защиту СИ и измеряемого объекта от влияния этих источников. Источники инструментальной погрешности, присущие конкретному экземпляру СИ, могут быть устранены путем его калибровки или ремонта. Источники погрешностей, связанные с неудачным взаимным расположением СИ могут быть устранены перед началом измерений.
Слайд 5
Погрешности измерений
Устранение систематических погрешностей
Одним из наиболее распространенных
способов исключения систематических погрешностей является способ замещения.
Он заключается
в том, что измеряемый объект заменяется известной мерой, находящейся в тех же условиях, в какой находился он сам.
Слайд 6
Погрешности измерений
Способ компенсации погрешности по знаку.
Измерение проводят
дважды так, чтобы известная по природе, но неизвестная по
размеру погрешность входила в результаты измерений с противоположными знаками. Погрешность исключается при вычислении среднего значения. В алгебраической форме это можно выразить следующим образом.
Слайд 7
Погрешности измерений
Случайные погрешности
Математические модели случайной погрешности.
Прислучайных погрешностях
результат каждого измерения Аi будет отличаться от истинного значения
Х измеряемой величины:Эту разность называют случайной погрешностью отдельного наблюдения.
Истинное значение Х нам неизвестно. Однако проведя большое количество наблюдений можно определить среднее значение
Слайд 8
Погрешности измерений
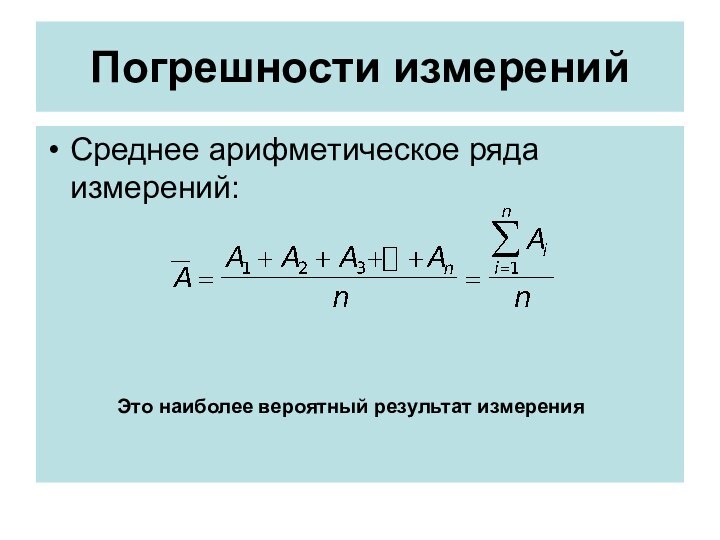
Среднее арифметическое ряда измерений:
Это наиболее вероятный
результат измерения
Слайд 9
Погрешности измерений
Гауссовский закон распределения
(в практике радиоизмерений наиболее распространён)
p(ΔX)
- плотность вероятности случайной погрешности
Слайд 10
Погрешности измерений
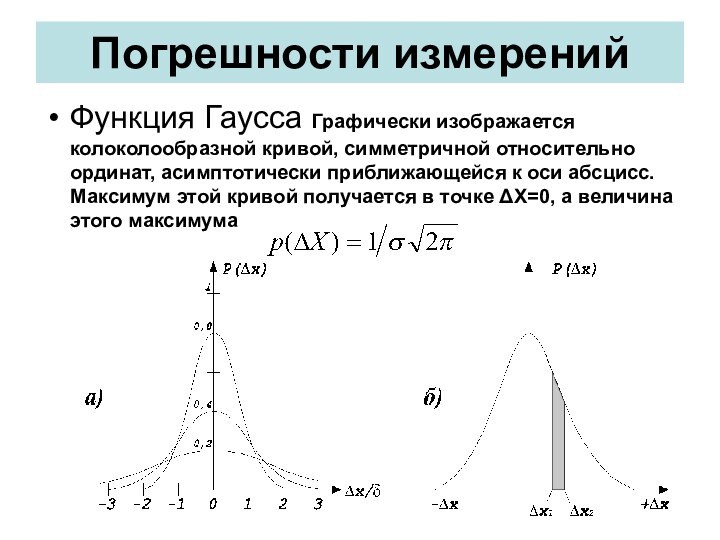
Функция Гаусса Графически изображается колоколообразной кривой, симметричной
относительно ординат, асимптотически приближающейся к оси абсцисс. Максимум этой
кривой получается в точке ΔХ=0, а величина этого максимума
Слайд 11
Погрешности измерений
Вероятность появления погрешности в пределах между ΔХ1
и ΔХ2 определяется площадью заштрихованного участка на предыдущем рис.
т.е. определённым интегралом от функции p(ΔХ):
Слайд 12
Погрешности измерений
Из таблиц, приведенных в математических справочниках, следует
что значение интеграла
Таким образом с вероятностью 0,683 случайные погрешности
измерения не выходят за пределы ±σ. С вероятностью 0,997 случайная погрешность находится в пределах ± 3σ, т.е. только 3 измерения из 1000 могут дать погрешность превышающую ± 3σ. Это соотношение называется законом трёх сигм.
Слайд 13
Погрешности измерений
Представленные ф-лы выведены из расчета, что n → ∞
На практике число измерений конечно. Однако, при увеличении числа
измеренийи Х сближаются и формула принимает вид;