Слайд 2
Задачи:
- определить область
применения формул комбинаторики;
- провести экспериментальный перебор вариантов построения
-
комбинаций заданного типа;
проанализировать результаты экспериментального перебора и
подсчета возможных комбинаций по формулам комбинаторики;
- дать советы, которые помогут при выигрыше в лотерею.
Слайд 3
Лотерея появилась на свете давно и, похоже, надолго.
Жребий бросали ещё библейские персонажи. Но первая лотерея в
её классическом понимании была проведена только в 16-ом веке в итальянском городе Флоренция. Называлась прародительница лотерей – Lotto de Firenze.
История возникновения понятия
Слайд 4
Примеры событий.
Рассмотрим несколько примеров событий.
1. Опыт – бросание
монеты; событие A – появление герба.
2. Опыт –
бросание трех монет; событие B – появление трех гербов.
3. Опыт передача группы из n сигналов; событие C – искажение хотя бы одного из них.
4. Опыт – выстрел по мишени; событие D – промах.
5. Опыт – вынимание наугад одной карты из колоды; событие Е – появление карты пиковой масти.
6. Тот же опыт, что в примере 5; событие F – появление короля.
7. Опыт – выбор билета на экзамене, событие G – появление четного номера билета.
8. Опыт – бросок мяча в кольцо баскетболистом, событие H – мяч оказывается в корзине.
Слайд 5
Примеры событий.
Опыт: 32 буквы разрезной азбуки смешали между
собой; наугад вынимается одна карточка, стоящая на ней буква
записывается, карточка возвращается обратно и смешивается с другими. Такой опыт производится 25 раз. Событие A состоит в том, что после 25 вынимания мы из этих букв получаем 1 строчку из песни посвящённой ВОВ "Идёт война священная". Событие A не является физически невозможным, но вероятность его настолько мала, что событие с такой вероятностью можно смело считать практически невозможным.
Слайд 6
Примеры событий.
Пример. Опыт: В фильме «Они сражались за
Родину», в бою выстрел в врага. Событие А –
попадание в врага. Противоположное событие А – непопадание в врага.
Слайд 7
Тиражные лотереи, или "лото"
Самая популярная форма лотереи -
это лото. Эта игра учреждается государством, как правило. Существенная
часть доходов от такой лотереи идет на нужды образования, спорта и т.п. Вы все хорошо знакомы с такими лотереями. Правила игры просты: Вам надо выбрать 6 любых чисел от 1 до 49, купить билет и обозначить в нем эти числа.
Слайд 8
Расчёт вероятности выигрыша.
Самый простой (и, наверное, единственный) способ
повысить свои шансы на выигрыш - покупать больше билетов
на тираж. Если Вы ставите на 2 комбинации чисел вместо одной - Ваши шансы увеличиваются вдвое! И так далее.
Слайд 9
Увидев в журнале «Домашний компьютер» конкурс, где надо
было угадать 2 числа из 100 для получения приза,
я задумалась: « А возможно ли выиграть в данной игре?»
И я решила провести эксперимент: попросила каждого ученика из нашего класса выбрать и зачеркнуть 2 числа из 100 из данной карточки. Перед заданием, я загадала два числа.
Слайд 10
Вывод: В результате получилось, что из 26 человек
никто не угадал 2 числа.
Мне стало интересно, а
существует ли лотерея с угадыванием чисел, в которой вероятность выигрыша больше.
Слайд 11
Я узнала, что раньше существовала лотерея ЛОТТО –
МИЛЛИОН. Чтобы получить большой выигрыш, надо было угадать 6
чисел из 49. Выигрывали карточки и с совпадением 5 и даже 4 номеров.
А сколько карточек Лото – Миллион нужно было купить и заполнить, чтобы на них оказались все комбинации по 6 номеров из 49 возможных, т. е. чтобы выиграть наверняка? 6
Слайд 12
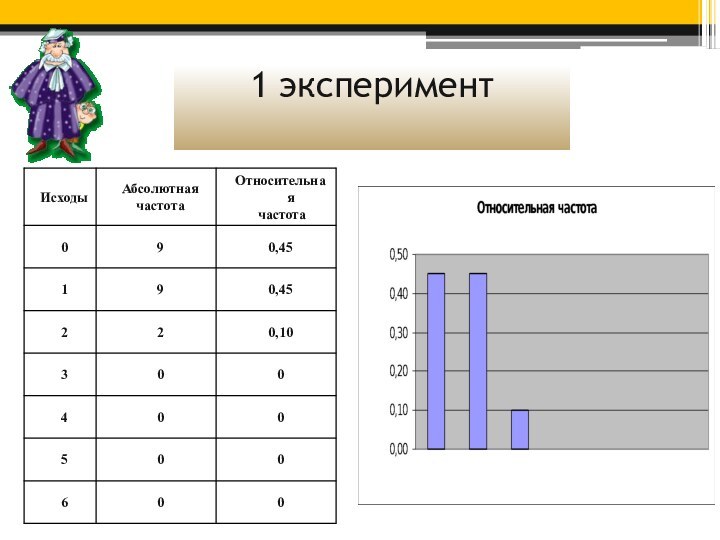
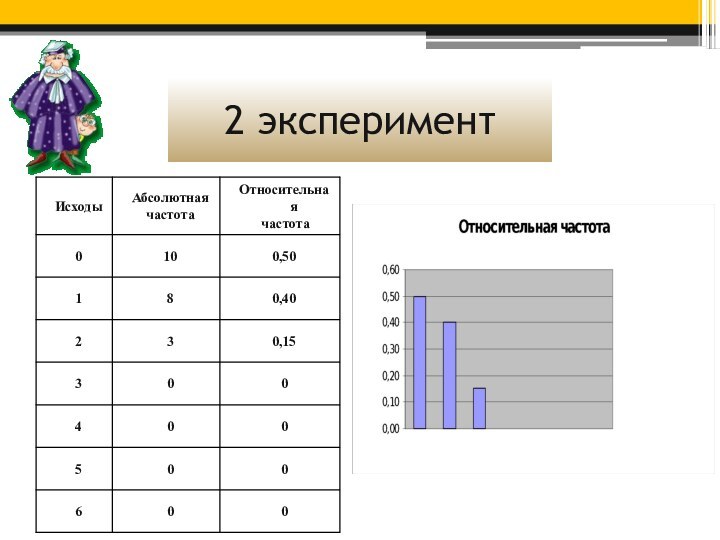
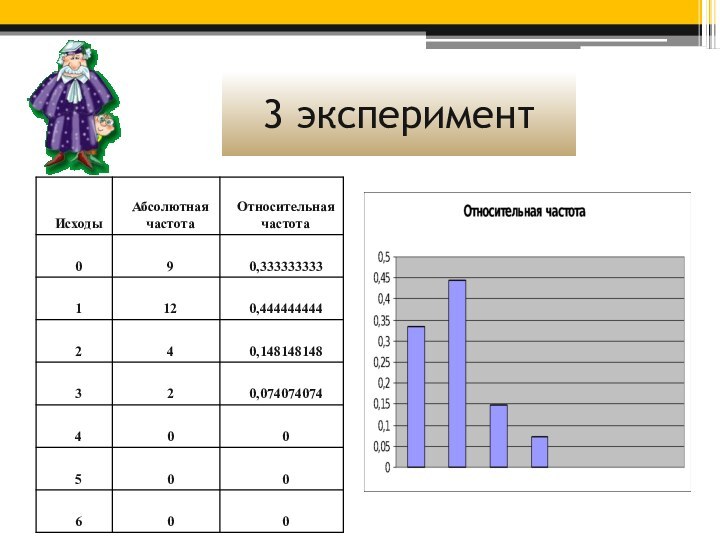
Но ведь кто-то же выигрывал! Я провела несколько
экспериментов в своем классе. Я попросила зачеркнуть в карточке
6 номеров из 49.
По результатам экспериментов я составила таблицы и гистограммы (столбчатую диаграмму). Абсолютная частота показывает, сколько раз в серии экспериментов наблюдалось данное событие.
Относительная частота (которую иногда называют просто частотой) показывает, какая доля экспериментов завершилась наступлением данного события.
Слайд 16
Вывод:
Отсюда следует, что вероятность проигрыша равна
Р3 +
Р2 + Р1 + Р0 ≈ 0,999012 Вероятность самого
крупного выигрыша равна -7
Р6 ≈ 0,0000000715 = 0, 7115 · 10
Вероятность самого маленького выигрыша Р4 =0,000969
Слайд 17
Выигрывайте в лото с нашими советами.
Подсказка 1:
используйте четные и нечетные числа
Подсказка 2: используйте нижние и
верхние числа
Подсказка 3: сбалансированная сумма
Подсказка 4: используйте неполные системы
Подсказка 5: играйте в пулах!
Знайте номера, которых стоит избегать - экономьте свои деньги!
Избегайте выбирать 5 последовательных чисел.
Избегайте выбирать все числа из одного десятка.
Избегайте геометрических фигур.
Избегайте повторяющихся цифр на конце.
Слайд 18
Заключение.
В своей работе я привела как примеры, так
и рекомендации, которые можно использовать в лотереях. С поставленными
задачами своей работы я справилась.
Думаю, что и цель в данной работе достигнута, так как после написания работы расширила и углубила свои знания по теме «Вероятность выигрыша в лотерею», познакомившись с формулами комбинаторики; исследовав различные способы решения комбинаторных задач.
Слайд 19
В перспективе на будущее
я планирую
эту работу
продолжить,
так как вероятность,
какого либо события
для меня очень интересна.