Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Визуализация многомерных пространств

Содержание

Где мы встречаем многомерные пространства? Одна из самых распространенных областей - анализ данных:
Визуализация многомерных пространствАвтор: Сугоняев Андрей, гр. 331 Где мы встречаем многомерные пространства? Одна из самых распространенных областей - анализ данных: Цель визуализации Цель – получить отображение данных в 2 или 3 МетодыРассмотрим методы, сопоставляющие точке в n-мерном пространстве точку в пространстве меньшей размерности: Метод главных компонент (PCA)Основной линейный метод понижения размерности – PCA – производит Максимизировать вариацию по векторуМинимизировать сумму расстояний от точки до ее проекции на данный вектор Записать x1 … xn как вектор-строкиРазместить вектор-строки в одной матрице X размером Шаг 2: Оцентрировать данныеНайти среднее по каждой колонкеВычесть вектор средних из каждой строки матрицы объектов-признаков Х Шаг 3: Вычислить матрицу ковариацииНайти матрицу ковариации С размера n × n Шаг 4: Найти собственные вектора и собственные числа матрицы СВычислить матрицу V Шаг 5: Проекция и реконструкцияВ матрицу Vreduced записать k вектор-колонок, соответствующих k 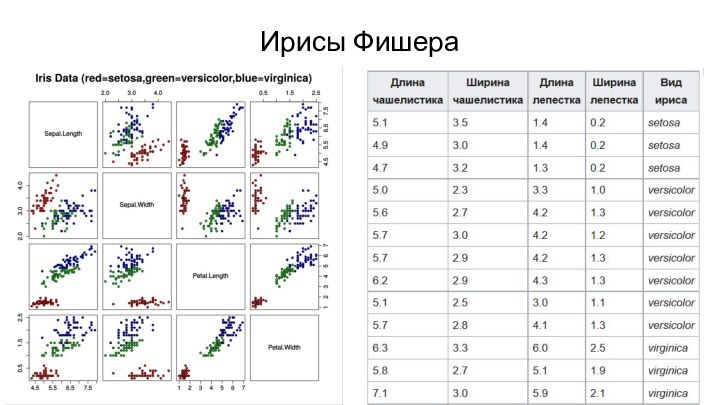Ирисы Фишера 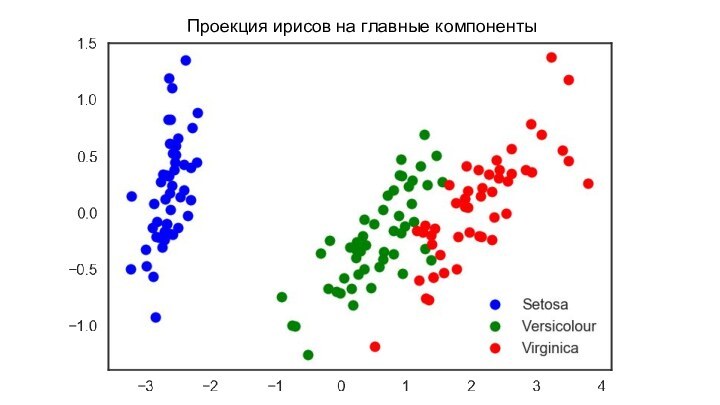Проекция ирисов на главные компоненты 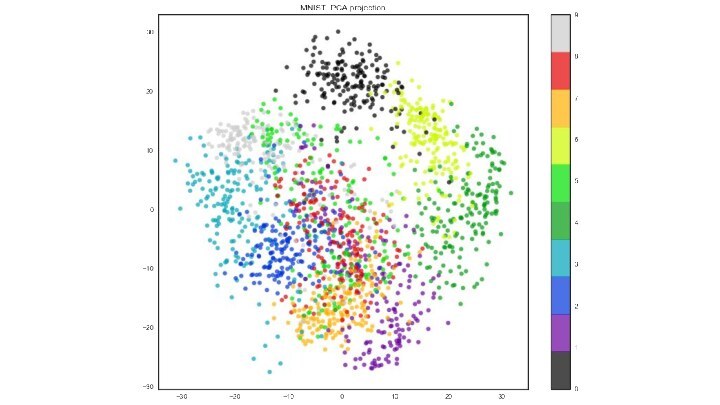MNIST (сокр. от Mixed National Institute of Standards and Technology) Почему такой плохой результат?Линейная комбинация объектов датасета не является рукописной цифрой.Значит объекты Нелинейные методыРассмотрим более простую модель и поставим задачу нелинейного понижения размерности:Задача — Гипотеза: малоразмерное представление сохраняет попарные расстояния между объектами. - расстояние Функционал качества: Ищем представления, апроксимирующие dij:Алгоритм: SMACOF (Scaling by MAjorizing a COmplicated Function) - стресс-функцияRepeatuntil Stochastic Neighbour Embedding (SNE)Гипотеза: В точности воспроизвести расстояния – слишком сложно. 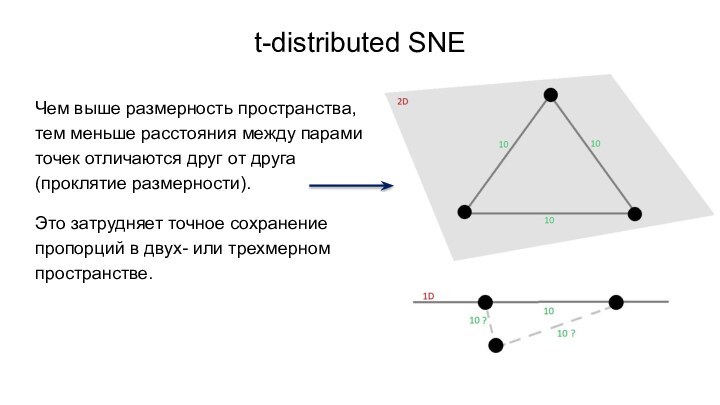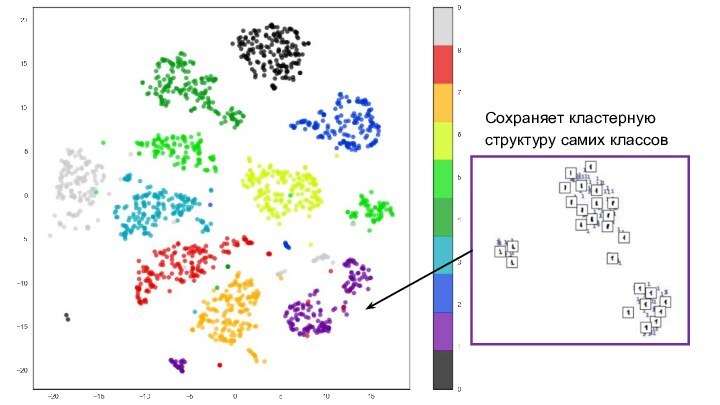Достаточно Функционал качества: Минимизируем разницу между распределениями расстояний с помощью дивергенции Кульбака-Лейблера:Алгоритм: (Стохастический) градиентный t-distributed SNEЧем выше размерность пространства, тем меньше расстояния между парами точек отличаются Значит нужно меньше штрафовать за увеличение пропорций в маломерном пространстве.Изменим распределение: Сохраняет кластерную структуру самих классов Сравнение методов Выводы Существует множество методов визуализации многомерных данных Выбор метода сильно зависит от Спасибо за внимание
Слайды презентации

Слайд 2 Где мы встречаем многомерные пространства?
Одна из самых

Где мы встречаем многомерные пространства? Одна из самых распространенных областей - анализ данных:

распространенных областей - анализ данных:

Слайд 3 Цель визуализации
Цель – получить отображение данных

Цель визуализации Цель – получить отображение данных в 2 или

в 2 или 3 мерном пространстве для дальнейшего изучения

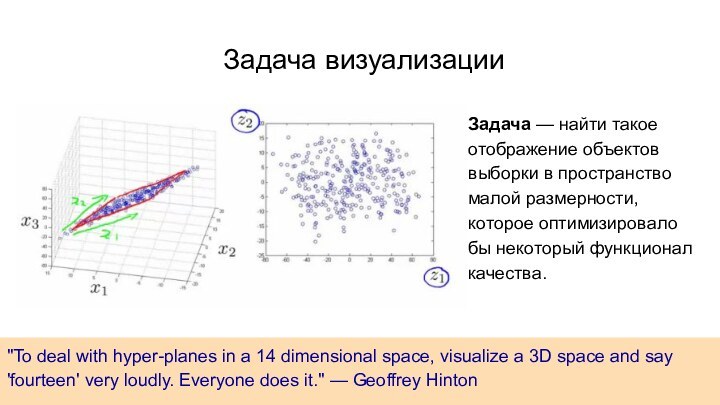
структурных особенностей и закономерностей этих данных.

Слайд 4 "To deal with hyper-planes in a 14 dimensional

space, visualize a 3D space and say 'fourteen' very

loudly. Everyone does it." — Geoffrey Hinton

Задача — найти такое отображение объектов выборки в пространство малой размерности, которое оптимизировало бы некоторый функционал качества.

Задача визуализации

Слайд 5 Методы
Рассмотрим методы, сопоставляющие точке в n-мерном пространстве точку

МетодыРассмотрим методы, сопоставляющие точке в n-мерном пространстве точку в пространстве меньшей размерности:

в пространстве меньшей размерности:


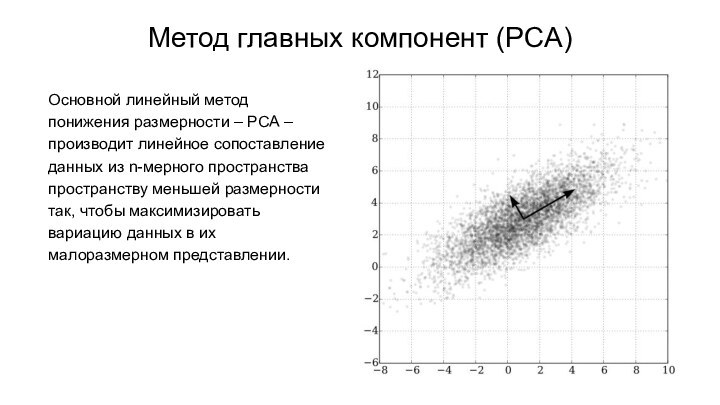
Слайд 6 Метод главных компонент (PCA)
Основной линейный метод понижения размерности

Метод главных компонент (PCA)Основной линейный метод понижения размерности – PCA –

– PCA – производит линейное сопоставление данных из n-мерного

пространства пространству меньшей размерности так, чтобы максимизировать вариацию данных в их малоразмерном представлении.

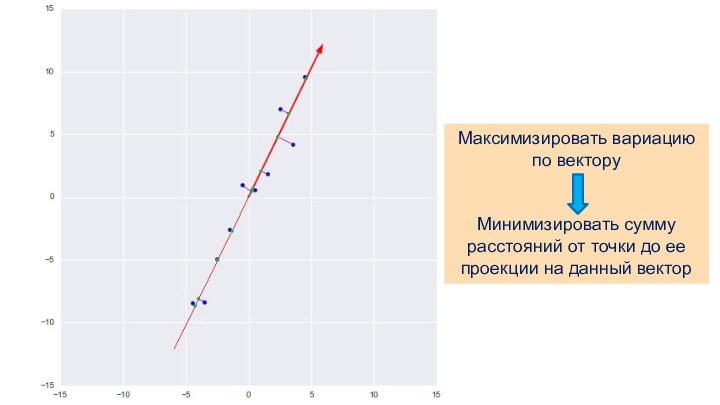
Слайд 7 Максимизировать вариацию по вектору


Минимизировать сумму расстояний от точки

Максимизировать вариацию по векторуМинимизировать сумму расстояний от точки до ее проекции на данный вектор

до ее проекции на данный вектор

Слайд 8
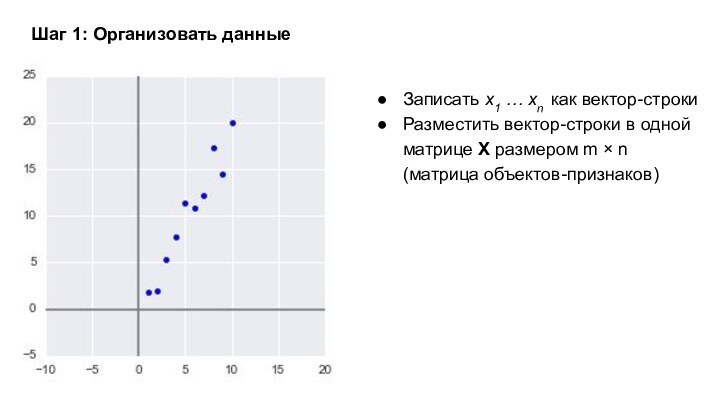
Записать x1 … xn как вектор-строки
Разместить вектор-строки в

Записать x1 … xn как вектор-строкиРазместить вектор-строки в одной матрице X

одной матрице X размером m × n (матрица объектов-признаков)

Шаг

1: Организовать данные

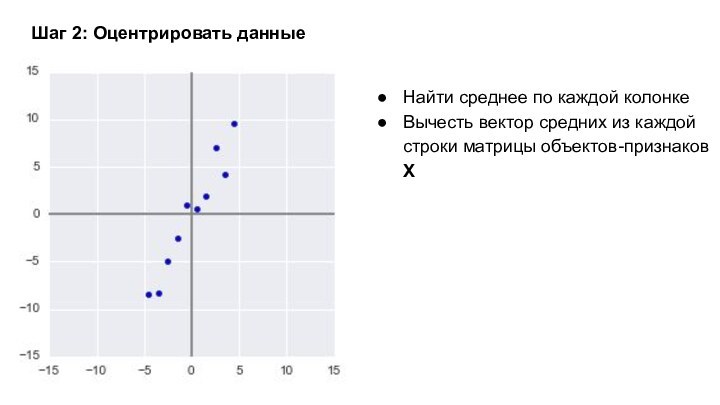
Слайд 9 Шаг 2: Оцентрировать данные
Найти среднее по каждой колонке
Вычесть

Шаг 2: Оцентрировать данныеНайти среднее по каждой колонкеВычесть вектор средних из каждой строки матрицы объектов-признаков Х

вектор средних из каждой строки матрицы объектов-признаков Х

Слайд 10 Шаг 3: Вычислить матрицу ковариации
Найти матрицу ковариации С

Шаг 3: Вычислить матрицу ковариацииНайти матрицу ковариации С размера n ×

размера n × n как:
C = 1⁄(n − 1)

XT X

Использование N − 1 вместо N обусловлено поправкой Бесселя

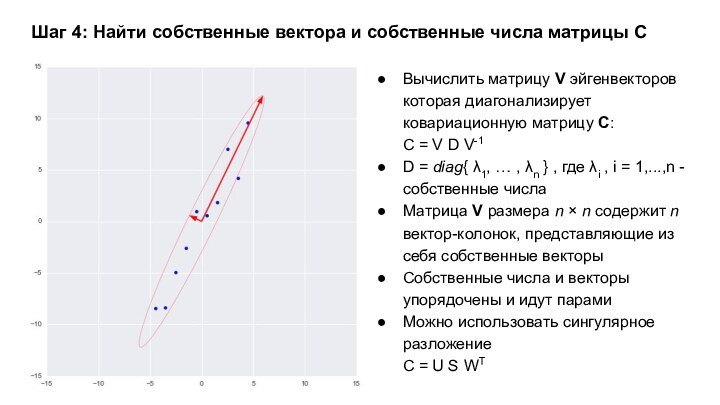
Слайд 11 Шаг 4: Найти собственные вектора и собственные числа

Шаг 4: Найти собственные вектора и собственные числа матрицы СВычислить матрицу

матрицы С
Вычислить матрицу V эйгенвекторов которая диагонализирует ковариационную матрицу

C:
C = V D V-1
D = diag{ λ1, … , λn } , где λi , i = 1,...,n - собственные числа
Матрица V размера n × n содержит n вектор-колонок, представляющие из себя собственные векторы
Собственные числа и векторы упорядочены и идут парами
Можно использовать сингулярное разложение
C = U S WT

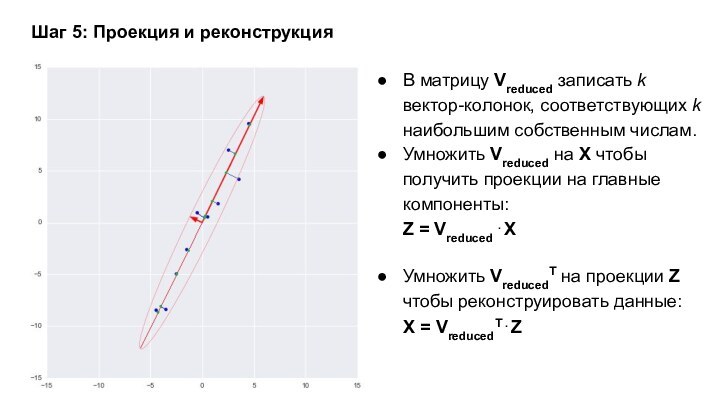
Слайд 12 Шаг 5: Проекция и реконструкция
В матрицу Vreduced записать

Шаг 5: Проекция и реконструкцияВ матрицу Vreduced записать k вектор-колонок, соответствующих

k вектор-колонок, соответствующих k наибольшим собственным числам.
Умножить Vreduced на

X чтобы получить проекции на главные компоненты:
Z = Vreduced . X

Умножить VreducedT на проекции Z чтобы реконструировать данные:
X = VreducedT . Z



Слайд 13 Ирисы Фишера

Ирисы Фишера

Слайд 14 Проекция ирисов на главные компоненты

Проекция ирисов на главные компоненты

Слайд 15 MNIST (сокр. от Mixed National Institute of Standards

MNIST (сокр. от Mixed National Institute of Standards and Technology)

and Technology)

Слайд 16

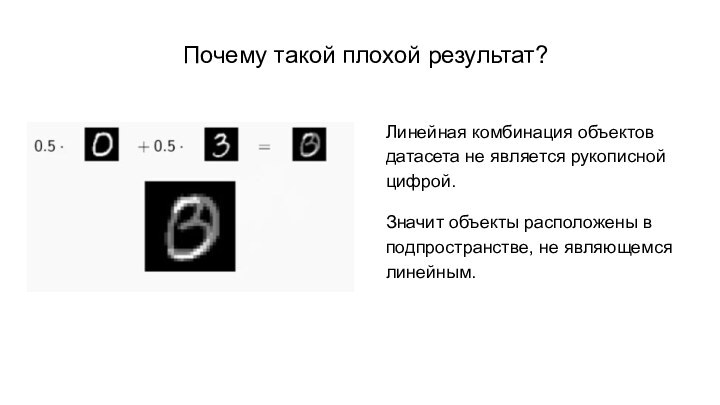
Слайд 17 Почему такой плохой результат?
Линейная комбинация объектов датасета не

Почему такой плохой результат?Линейная комбинация объектов датасета не является рукописной цифрой.Значит

является рукописной цифрой.
Значит объекты расположены в подпространстве, не являющемся

линейным.

Слайд 18 Нелинейные методы
Рассмотрим более простую модель и поставим задачу

Нелинейные методыРассмотрим более простую модель и поставим задачу нелинейного понижения размерности:Задача

нелинейного понижения размерности:

Задача — найти отображение объектов выборки в

пространство малой размерности, которое оптимизировало бы функционал качества.
При этом мы не ограничены линейными отображениями.

Слайд 19 Гипотеза: малоразмерное представление сохраняет попарные расстояния между объектами.

Гипотеза: малоразмерное представление сохраняет попарные расстояния между объектами. - расстояние

- расстояние между xi и xj

- евклидово расстояние между малоразмерными представлениями


Многомерное шкалирование

Слайд 20
Функционал качества:
Ищем представления, апроксимирующие dij:




Алгоритм: SMACOF (Scaling by

Функционал качества: Ищем представления, апроксимирующие dij:Алгоритм: SMACOF (Scaling by MAjorizing a COmplicated Function) - стресс-функцияRepeatuntil

MAjorizing a COmplicated Function)

- стресс-функция
Repeat



until

Слайд 21 Stochastic Neighbour Embedding (SNE)
Гипотеза: В точности воспроизвести расстояния

Stochastic Neighbour Embedding (SNE)Гипотеза: В точности воспроизвести расстояния – слишком сложно.

– слишком сложно. Достаточно сохранения пропорций.



Опишем объекты нормированными расстояниями

до остальных объектов:


Слайд 22
Функционал качества:
Минимизируем разницу между распределениями расстояний с помощью

Функционал качества: Минимизируем разницу между распределениями расстояний с помощью дивергенции Кульбака-Лейблера:Алгоритм: (Стохастический)

дивергенции Кульбака-Лейблера:



Алгоритм: (Стохастический) градиентный спуск
Repeat


until convergence

Слайд 23 t-distributed SNE
Чем выше размерность пространства, тем меньше расстояния

t-distributed SNEЧем выше размерность пространства, тем меньше расстояния между парами точек

между парами точек отличаются друг от друга (проклятие размерности).
Это

затрудняет точное сохранение пропорций в двух- или трехмерном пространстве.

Слайд 24 Значит нужно меньше штрафовать за увеличение пропорций в

Значит нужно меньше штрафовать за увеличение пропорций в маломерном пространстве.Изменим распределение:

маломерном пространстве.
Изменим распределение:

Слайд 25 Сохраняет кластерную структуру самих классов

Сохраняет кластерную структуру самих классов

Слайд 26 Сравнение методов

Сравнение методов

Слайд 27 Выводы
Существует множество методов визуализации многомерных данных
Выбор

Выводы Существует множество методов визуализации многомерных данных Выбор метода сильно зависит

метода сильно зависит от конкретной задачи
Ключевым фактором при

выборе метода является балансирование между большей потерей информации и лучшей визуализацией структуры данных
  • Имя файла: vizualizatsiya-mnogomernyh-prostranstv.pptx
  • Количество просмотров: 160
  • Количество скачиваний: 0
- Предыдущая Франция в 1815-1847 гг
Следующая - Налоговая система России. Законодательство о налогах и сборах

Похожие презентации

Проект Использование дидактических игр в процессе формирования элементарных математических представлений у дошкольников проект по математике (подготовительная группа) Проект Использование дидактических игр в процессе формирования элементарных математических представлений у дошкольников проект по математике (подготовительная группа) 116
Презентация по математике Серединный перпендикуляр (5 класс) Презентация по математике Серединный перпендикуляр (5 класс) 140
Упрощение выражений Упрощение выражений 109
Математика 1 класс счёт Математика 1 класс счёт 96
Упрощение выражений Упрощение выражений 118
Декартовы произведения Декартовы произведения 105
Как читать графики Как читать графики 163
Прямоугольный треугольник Прямоугольный треугольник 123
Проект Проект 101
Арифметические действия с числами (3 класс) Арифметические действия с числами (3 класс) 103
Решение текстовых задач 5 класс Решение текстовых задач 5 класс 102
Методическая разработка по игре Геометрическая карусель презентация к уроку по математике (младшая группа) Методическая разработка по игре Геометрическая карусель презентация к уроку по математике (младшая группа) 120
Презентация к урокуСложение и вычитание в пределах 20 презентация к уроку по математике (1 класс) по теме Презентация к урокуСложение и вычитание в пределах 20 презентация к уроку по математике (1 класс) по теме 49
Кенгуру-1 олимпиадные задания по математике Кенгуру-1 олимпиадные задания по математике 145
Презентация к уроку Свойства вычитания 1 класс. УМК Начальная школа 21 века Презентация к уроку Свойства вычитания 1 класс. УМК Начальная школа 21 века 201
Презентация по математике Столько же. Больше. Меньше Презентация по математике Столько же. Больше. Меньше 101
Программа для работы с тригонометрическими функциями Программа для работы с тригонометрическими функциями 96
Презентация по математика 5 класс Презентация по математика 5 класс 106
Элементы статистики Элементы статистики 110
Урок математики в 4 классе презентация к уроку по математике (4 класс) по теме Урок математики в 4 классе презентация к уроку по математике (4 класс) по теме 102
Построение графиков функций, содержащих знак модуля Построение графиков функций, содержащих знак модуля 88
Конспект + презентация урока математики по теме: Таблица сложения однозначных чисел 1 класс, ПНШ. план-конспект урока по математике (1 класс) Конспект + презентация урока математики по теме: Таблица сложения однозначных чисел 1 класс, ПНШ. план-конспект урока по математике (1 класс) 110
Веселая математика презентация к уроку по математике (старшая группа) Веселая математика презентация к уроку по математике (старшая группа) 100
Презентации по математике на тему Тригонометрия Презентации по математике на тему Тригонометрия 118
Методы решения квадратных уравнений Методы решения квадратных уравнений 101
Числа в различных системах счисления Числа в различных системах счисления 116
Конспект урока Окружность и круг 2 класс план-конспект урока по математике (2 класс) Конспект урока Окружность и круг 2 класс план-конспект урока по математике (2 класс) 124
Дидактическая игра по ФЭМП для детей во второй младшей группе презентация по математике Дидактическая игра по ФЭМП для детей во второй младшей группе презентация по математике 180
Компоненты действия деления презентация к уроку по математике (2 класс) по теме Компоненты действия деления презентация к уроку по математике (2 класс) по теме 104
Площади многоугольников Площади многоугольников 129