- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку по математике по теме Многогранники (призма, параллелепипед, пирамида) их свойства
Содержание
- 2. Железнодорожный вокзалЗдание «Детского дома творчества»
- 4. «МНОГОГРАННИКИ В ПРОФЕССИИ ПРОДАВЦА»
- 5. "В стране многогранников"
- 6. 1-й тур «Вопрос – Ответ» 2-й тур «Оцени себя» 3-й тур «Домашнее задание»"В стране многогранников"
- 7. ОЦЕНОЧНЫЙ ЛИСТ
- 8. 13-15 баллов – «5» (отлично)11-12 баллов –
- 9. 1 тур "Вопрос-ответ" Командам предлагается выбрать номер
- 10. ВОПРОСЫ И ОТВЕТЫ К 1-МУ ТУРУ «ВОПРОС
- 11. "Вопрос-ответ"
- 12. ЧТО ТАКОЕ ПРИЗМА (ОСНОВАНИЯ ПРИЗМЫ, БОКОВЫЕ ГРАНИ,
- 13. ЧТО ТАКОЕ ВЫСОТА ПРИЗМЫ? ДИАГОНАЛЬ? Высотой призмы
- 14. ЧТО ПРЕДСТАВЛЯЕТ БОКОВАЯ ПОВЕРХНОСТЬ ПРИЗМЫ? Боковой поверхностью призмы называется сумма площадей боковых граней.
- 15. КАКАЯ ПРИЗМА НАЗЫВАЕТСЯ ПРЯМОЙ? Призма называется
- 16. ЧЕМУ РАВНА ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПРИЗМЫ?
- 17. ЧЕМУ РАВЕН ОБЪЕМ ПРИЗМЫ? Объем призмы
- 18. СВОЙСТВА ПРИЗМЫ? Основания призмы равны.
- 19. ЧТО ТАКОЕ ПАРАЛЛЕЛЕПИПЕД? ОБЪЯСНИТЕ ПО МОДЕЛИ (РИСУНКУ)
- 20. В ЧЕМ ЗАКЛЮЧАЕТСЯ СВОЙСТВО ПРОТИВОЛЕЖАЩИХ ГРАНЕЙ У ПАРАЛЛЕЛЕПИПЕДА? У параллелепипеда противолежащие грани параллельны и равны
- 21. СВОЙСТВО ДИАГОНАЛЕЙ ПАРАЛЛЕЛЕПИПЕДА Диагонали параллелепипеда пересекаются в
- 22. ЧЕМУ РАВЕН КВАДРАТ ЛЮБОЙ ДИАГОНАЛИ В ПРЯМОУГОЛЬНОМ
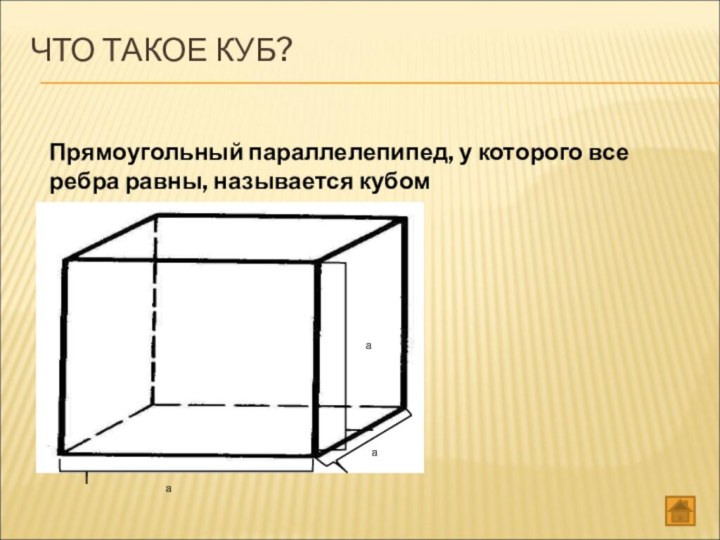
- 23. ЧТО ТАКОЕ КУБ? Прямоугольный параллелепипед, у которого все ребра равны, называется кубом
- 24. ЧЕМУ РАВЕН ОБЪЕМ ПАРАЛЛЕЛЕПИПЕДА? Объем прямоугольного параллелепипеда равен произведению трех его измерений:
- 25. ЧЕМУ РАВЕН ОБЪЕМ КУБА? Объем куба равен:
- 26. ЧТО ТАКОЕ ПИРАМИДА (ОСНОВАНИЕ ПИРАМИДЫ, БОКОВЫЕ ГРАНИ,
- 27. КАКАЯ ПИРАМИДА НАЗЫВАЕТСЯ ПРАВИЛЬНОЙ? Пирамида называется
- 28. ЧТО НАЗЫВАЕТСЯ АПОФЕМОЙ ПРАВИЛЬНОЙ ПИРАМИДЫ? Высота боковой
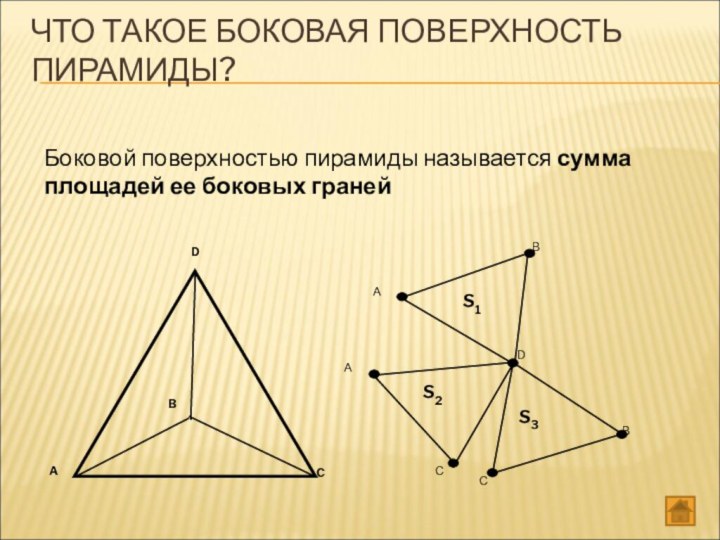
- 29. ЧТО ТАКОЕ БОКОВАЯ ПОВЕРХНОСТЬ ПИРАМИДЫ? Боковой поверхностью пирамиды называется сумма площадей ее боковых граней
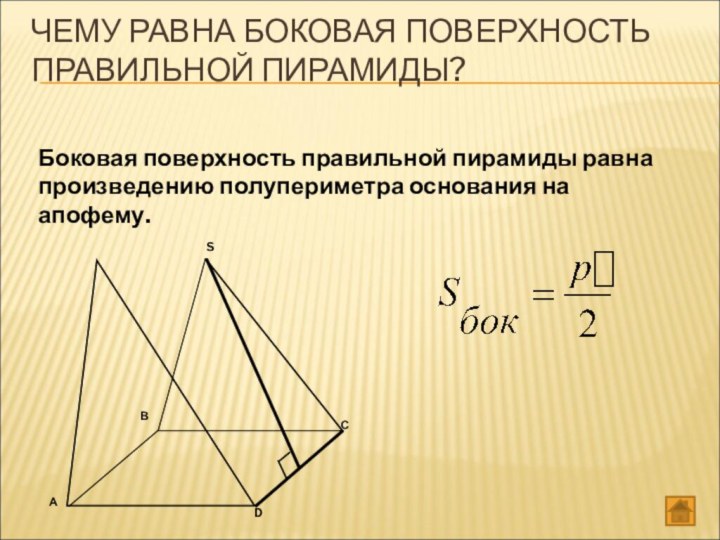
- 30. ЧЕМУ РАВНА БОКОВАЯ ПОВЕРХНОСТЬ ПРАВИЛЬНОЙ ПИРАМИДЫ? Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.
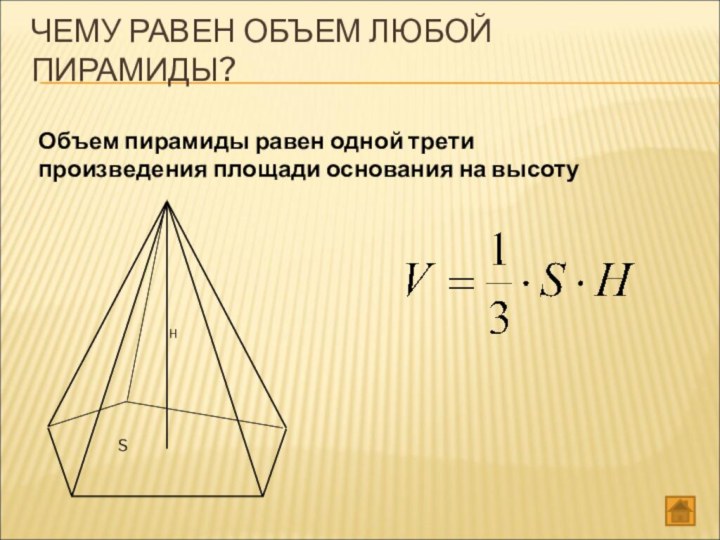
- 31. ЧЕМУ РАВЕН ОБЪЕМ ЛЮБОЙ ПИРАМИДЫ? Объем пирамиды равен одной трети произведения площади основания на высоту
- 32. ЧТО ТАКОЕ УСЕЧЕННАЯ ПИРАМИДА? (ОБЪЯСНИТЕ) Плоскость, параллельная
- 33. Физкульт минутка
- 34. 2 тур "Оцени себя" Участникам команды предлагается
- 35. 2-Й ТУР «ОЦЕНИ СЕБЯ»Задачи на «5»:1.В правильной
- 36. 06:00543107
- 37. *Мир правильных многогранников*Платоновы тела*Правильные многогранники в различных науках3 тур «Домашнее задание"
- 38. ДОМАШНЕЕ ЗАДАНИЕ:Обзор информационного материала к теме: «Тела вращения» http://www.pm298.ru/stereom2.phphttp://www.ref.by/refs/49/33147/1.htmlhttp://algolist.manual.ru/maths/geom/equation/sphere.phphttp://www.bymath.net/studyguide/geo/sec/geo18.htm
- 39. Скачать презентацию
- 40. Похожие презентации
Железнодорожный вокзалЗдание «Детского дома творчества»






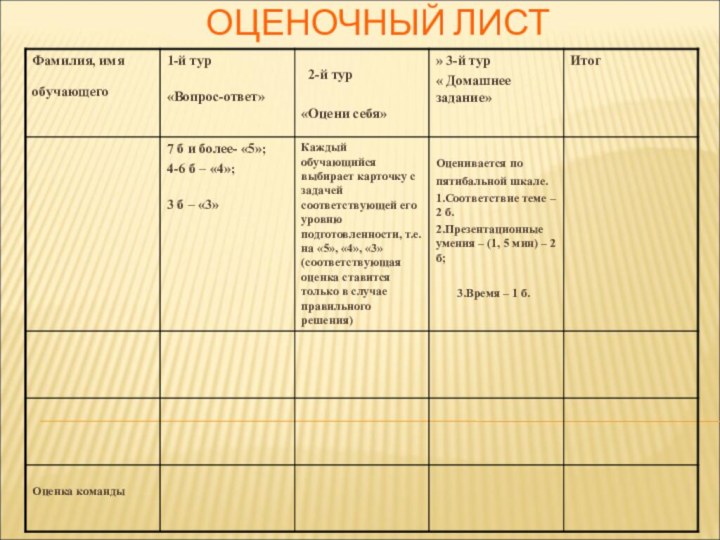


















Слайд 8
13-15 баллов – «5» (отлично)
11-12 баллов – «4»
(хорошо)
8-10 баллов – «3» (удовлетворительно)
Критерии оценок
Слайд 9
1 тур "Вопрос-ответ"
Командам предлагается выбрать номер вопроса.
Правильный ответ приносит команде 1 балл. Неверный ответ –
0 баллов и право ответа переходит к другой команде. Соблюдается правило поднятой руки.Критерии оценок:
- 7 баллов и более - «5»,
- 4 – 6 баллов – «4»,
- 3 балла и меньше - «3»
Слайд 10 ВОПРОСЫ И ОТВЕТЫ К 1-МУ ТУРУ «ВОПРОС –
ОТВЕТ»
Вопросы по теме «Призма»
Что такое призма (основания призмы, боковые
грани, ребра)? Объясните по модели (рисунку).
2. Что такое высота призмы? Диагональ?
3. Что представляет боковая поверхность призмы?
4. Какая призма называется прямой?
5. Чему равна площадь боковой поверхности призмы?
6. Чему равен объем призмы?
7. Свойства призмы?Вопросы по теме «Параллелепипед» 8. Что такое параллелепипед? Объясните по модели (рисунку). 9. В чем заключается свойство противолежащих граней у параллелепипеда? 10. Свойство диагоналей параллелепипеда. 11. Чему равен квадрат любой диагонали в прямоугольном параллелепипеде? 12. Что такое куб? 13. Чему равен объем параллелепипеда? 14. Чему равен объем куба?
Вопросы по теме «Пирамида» 15. Что такое пирамида (основание пирамиды, боковые грани, ребра, высота)? Объясните по модели (рисунку). 16. Какая пирамида называется правильной? 17. Что называется апофемой правильной пирамиды? 18. Что такое боковая поверхность пирамиды? 19. Чему равна боковая поверхность правильной пирамиды? 20. Чему равен объем любой пирамиды? 21. Что такое усеченная пирамида? (объясните).
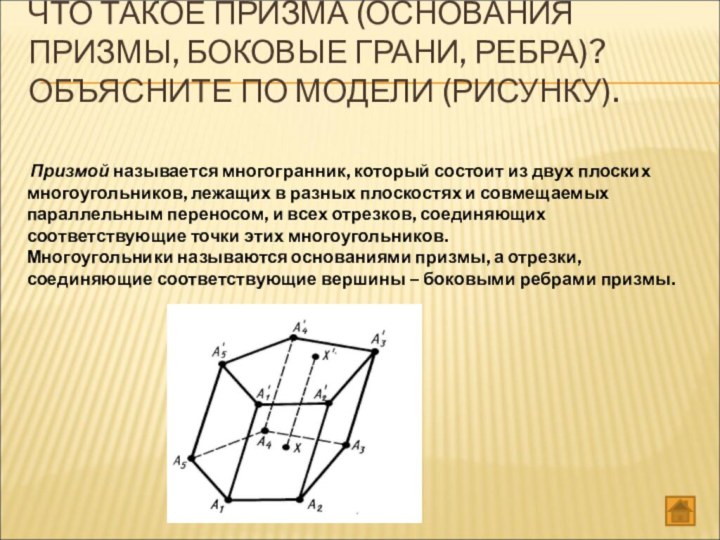
Слайд 12 ЧТО ТАКОЕ ПРИЗМА (ОСНОВАНИЯ ПРИЗМЫ, БОКОВЫЕ ГРАНИ, РЕБРА)?
ОБЪЯСНИТЕ ПО МОДЕЛИ (РИСУНКУ).
Призмой называется многогранник, который
состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников.Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие вершины – боковыми ребрами призмы.
Слайд 13
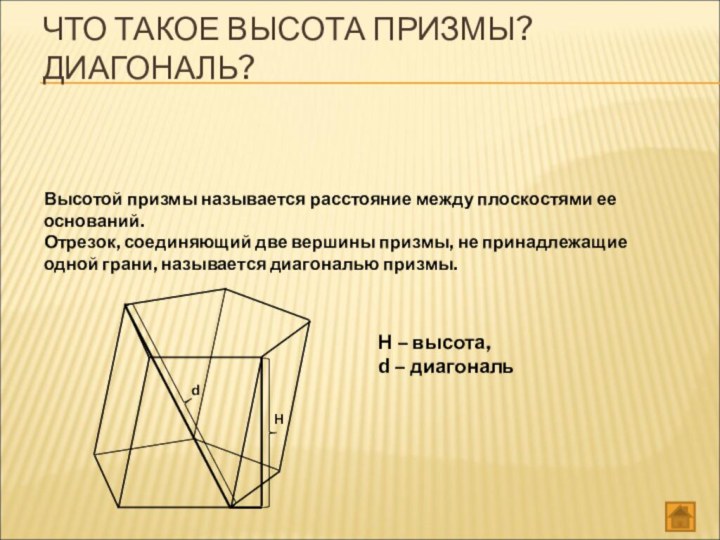
ЧТО ТАКОЕ ВЫСОТА ПРИЗМЫ? ДИАГОНАЛЬ?
Высотой призмы называется расстояние
между плоскостями ее оснований.
Отрезок, соединяющий две вершины призмы, не
принадлежащие одной грани, называется диагональю призмы.Н – высота,
d – диагональ
Слайд 14
ЧТО ПРЕДСТАВЛЯЕТ БОКОВАЯ ПОВЕРХНОСТЬ ПРИЗМЫ?
Боковой поверхностью
призмы называется сумма площадей боковых граней.
Слайд 15
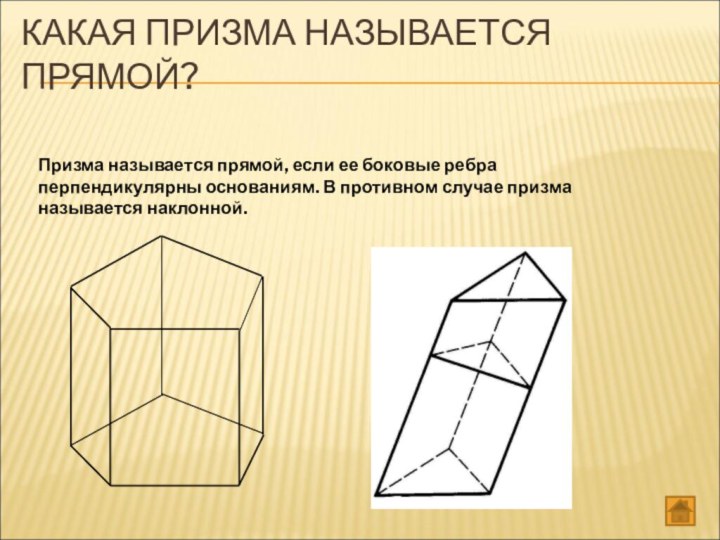
КАКАЯ ПРИЗМА НАЗЫВАЕТСЯ ПРЯМОЙ?
Призма называется прямой, если
ее боковые ребра перпендикулярны основаниям. В противном случае призма
называется наклонной.
Слайд 16
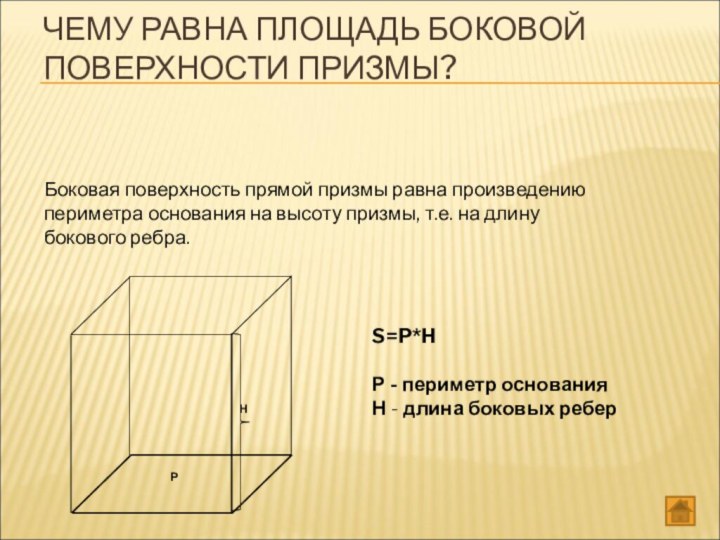
ЧЕМУ РАВНА ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПРИЗМЫ?
Боковая поверхность
прямой призмы равна произведению периметра основания на высоту призмы,
т.е. на длину бокового ребра.S=P*H
Р - периметр основания
Н - длина боковых ребер
Слайд 17
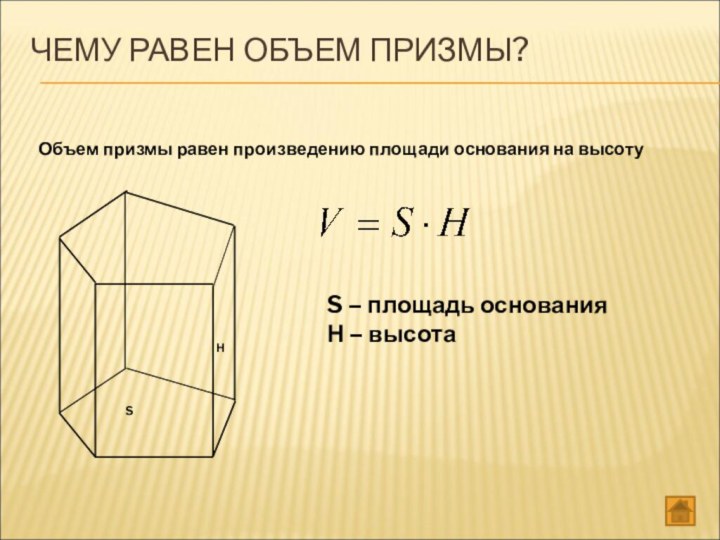
ЧЕМУ РАВЕН ОБЪЕМ ПРИЗМЫ?
Объем призмы равен произведению
площади основания на высоту
S – площадь основания
Н –
высота
Слайд 18
СВОЙСТВА ПРИЗМЫ?
Основания призмы равны.
У призмы
основания лежат в параллельных плоскостях.
У призмы боковые ребра
параллельны и равны.
Слайд 19
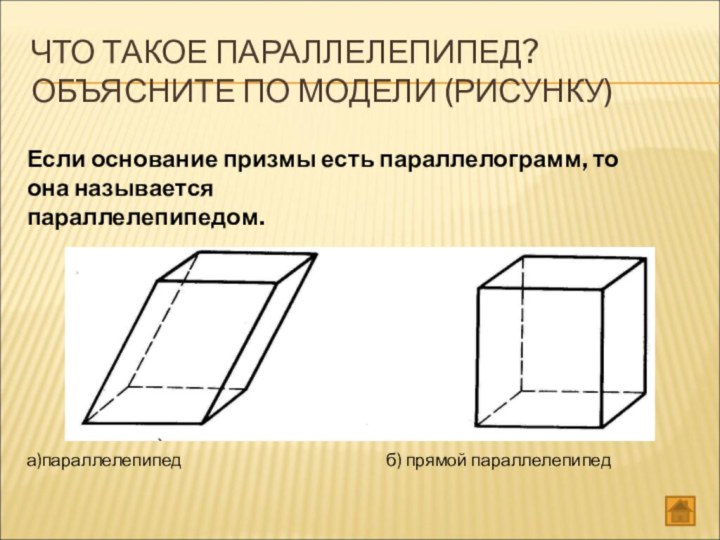
ЧТО ТАКОЕ ПАРАЛЛЕЛЕПИПЕД? ОБЪЯСНИТЕ ПО МОДЕЛИ (РИСУНКУ)
Если основание
призмы есть параллелограмм, то она называется
параллелепипедом.
а)параллелепипед
б) прямой параллелепипед
Слайд 20
В ЧЕМ ЗАКЛЮЧАЕТСЯ СВОЙСТВО ПРОТИВОЛЕЖАЩИХ ГРАНЕЙ У ПАРАЛЛЕЛЕПИПЕДА?
У
параллелепипеда противолежащие грани
параллельны и равны
Слайд 21
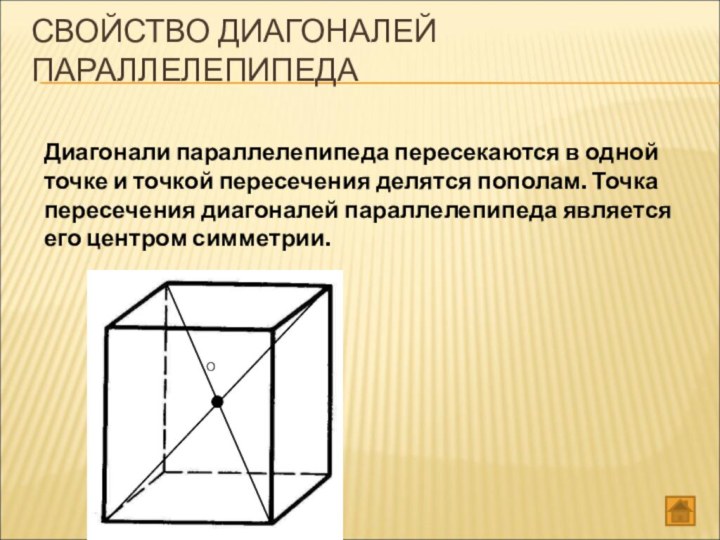
СВОЙСТВО ДИАГОНАЛЕЙ ПАРАЛЛЕЛЕПИПЕДА
Диагонали параллелепипеда пересекаются в одной точке
и точкой пересечения делятся пополам. Точка пересечения диагоналей параллелепипеда
является его центром симметрии.
Слайд 22
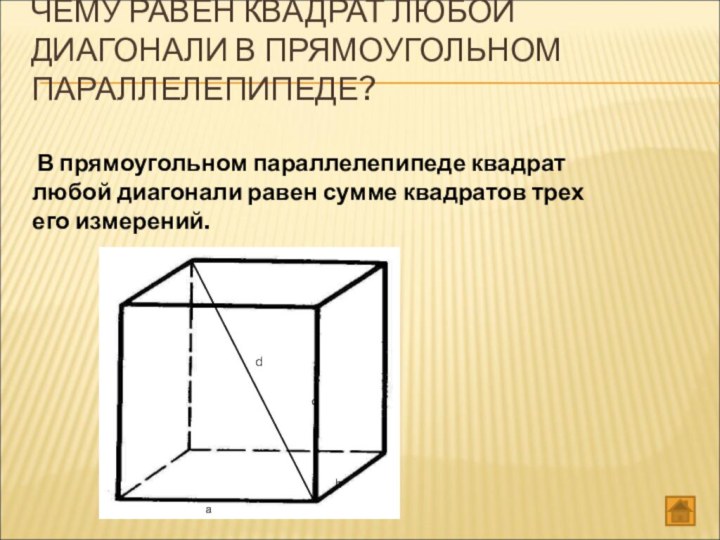
ЧЕМУ РАВЕН КВАДРАТ ЛЮБОЙ ДИАГОНАЛИ В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ?
В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов
трех его измерений.
Слайд 24
ЧЕМУ РАВЕН ОБЪЕМ ПАРАЛЛЕЛЕПИПЕДА?
Объем прямоугольного параллелепипеда равен
произведению трех его измерений:
Слайд 26 ЧТО ТАКОЕ ПИРАМИДА (ОСНОВАНИЕ ПИРАМИДЫ, БОКОВЫЕ ГРАНИ, РЕБРА,
ВЫСОТА)? ОБЪЯСНИТЕ ПО МОДЕЛИ (РИСУНКУ)
Пирамидой называется многогранник, который состоит
из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания – вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.Отрезки, соединяющие вершину пирамиды с вершинами основания, называют боковыми ребрами.
Каждая боковая грань – треугольник.
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Прямоугольная пирамида называется также тетраэдром.
H - высота
SA; SB; SC – ребра
ABC – основание
ASO; ASC; BSC – боковые грани
Слайд 27
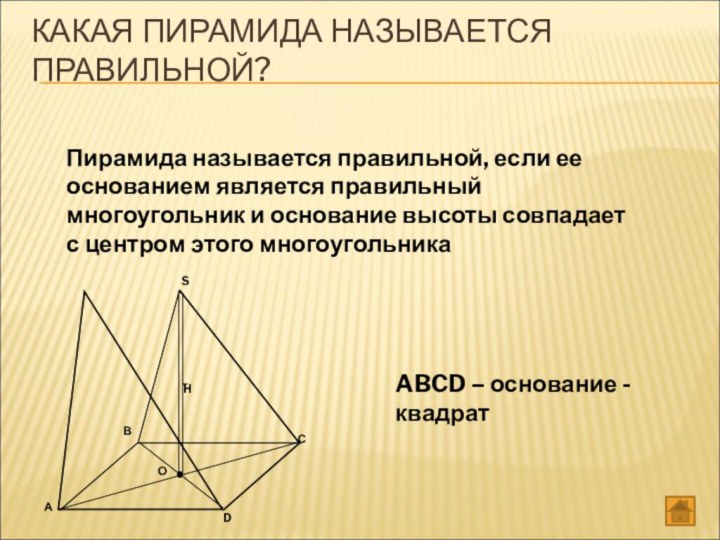
КАКАЯ ПИРАМИДА НАЗЫВАЕТСЯ ПРАВИЛЬНОЙ?
Пирамида называется правильной, если
ее основанием является правильный многоугольник и основание высоты совпадает
с центром этого многоугольникаABCD – основание - квадрат
Слайд 28
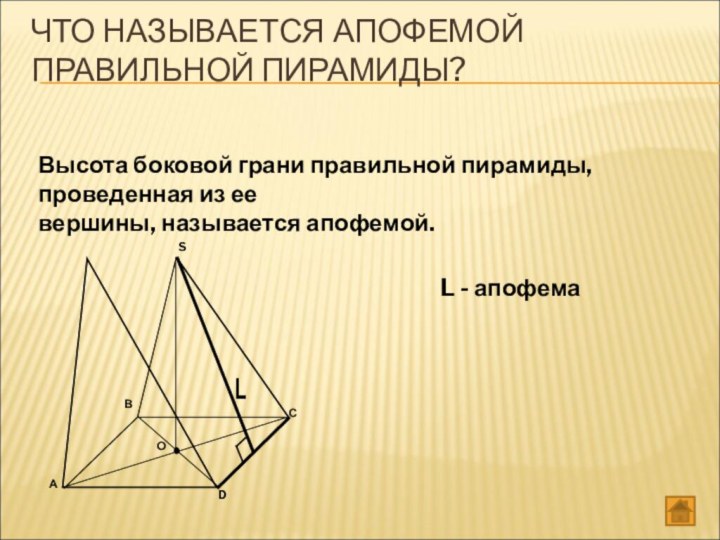
ЧТО НАЗЫВАЕТСЯ АПОФЕМОЙ ПРАВИЛЬНОЙ ПИРАМИДЫ?
Высота боковой грани правильной
пирамиды, проведенная из ее
вершины, называется апофемой.
L -
апофемаL
Слайд 29
ЧТО ТАКОЕ БОКОВАЯ ПОВЕРХНОСТЬ ПИРАМИДЫ?
Боковой поверхностью пирамиды
называется сумма площадей ее боковых граней
Слайд 30
ЧЕМУ РАВНА БОКОВАЯ ПОВЕРХНОСТЬ ПРАВИЛЬНОЙ ПИРАМИДЫ?
Боковая поверхность правильной
пирамиды равна произведению полупериметра основания на апофему.
Слайд 31
ЧЕМУ РАВЕН ОБЪЕМ ЛЮБОЙ ПИРАМИДЫ?
Объем пирамиды равен одной
трети произведения площади основания на высоту
Слайд 32
ЧТО ТАКОЕ УСЕЧЕННАЯ ПИРАМИДА? (ОБЪЯСНИТЕ)
Плоскость, параллельная плоскости основания
пирамиды и пересекающая ее боковые ребра, отсекает от нее
подобную пирамиду.Нижняя часть представляет собой многогранник, который называется усеченной пирамидой.
Грани усеченной пирамиды, лежащие в параллельных плоскостях называются основаниями; остальные грани называются боковыми гранями. Основания усеченной пирамиды представляют собой подобные многоугольники, боковые грани – трапеции.
Слайд 34
2 тур "Оцени себя"
Участникам команды предлагается несколько
карточек с задачами на «5», «4» и «3», где
каждый член команды по своим способностям выбирает нужную карточку.Время – 7 минут
Слайд 35
2-Й ТУР «ОЦЕНИ СЕБЯ»
Задачи на «5»:
1.В правильной четырехугольной
призме площадь основания 144см2, а высота 14см.
Найдите диагональ призмы.2.Кирпич размером 25х12х6,5 см имеет массу 3,51 кг. Найдите его плотность.
3.Основание пирамиды – прямоугольник со сторонами 9м и 12м, все боковые ребра равны 12,5м. Найдите объем пирамиды
Задачи на «4»:
1.Найдите объем правильной треугольной призмы, если площадь ее основания равна 17см2, а высота 9см.
2.Вычислите объем прямоугольного параллелепипеда, если его измерения равны 5см, 6см, 7см.
3.Найдите объем правильной четырехугольной пирамиды, если ее сторона основания равна 3см, а высота 12см.
Задачи на «3»:
1.Постройте треугольную призму. Обозначьте ее. Назовите все вершины, ребра, грани.
2.Постройте прямой параллелепипед, обозначьте его. Назовите вершины, ребра, грани.
3.Постройте прямой параллелепипед, обозначьте его. Назовите вершины, ребра, грани.





























