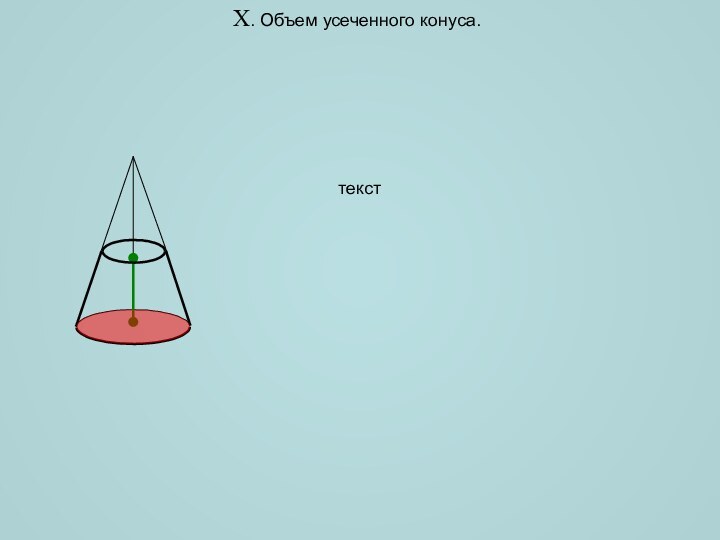
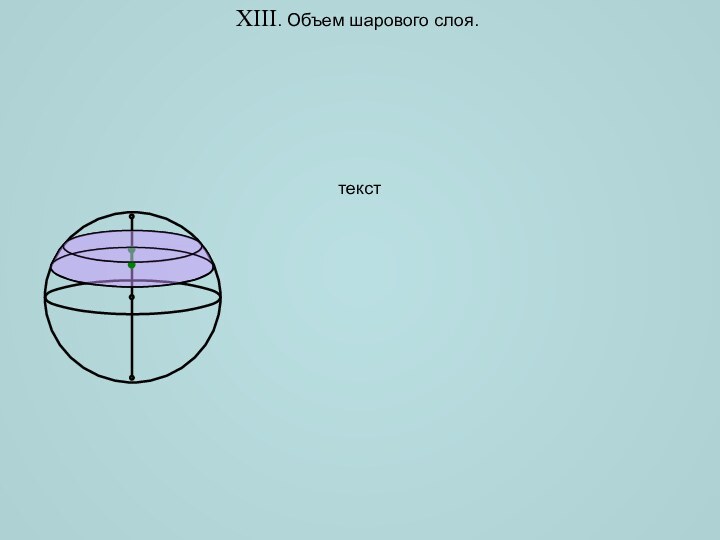
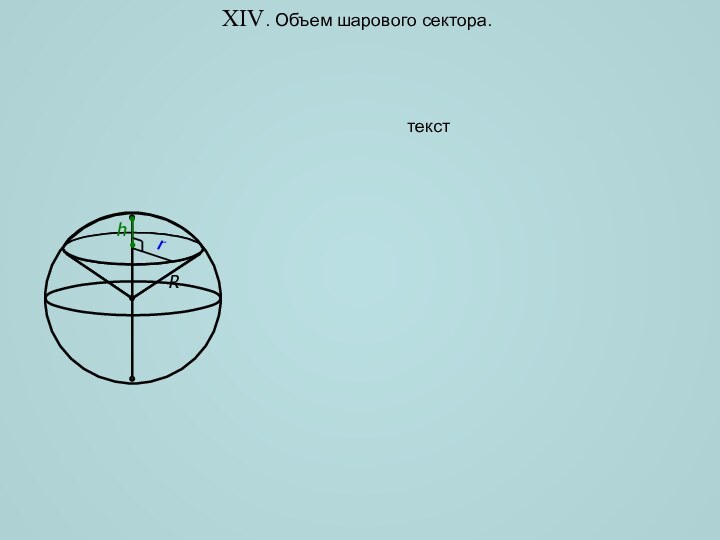
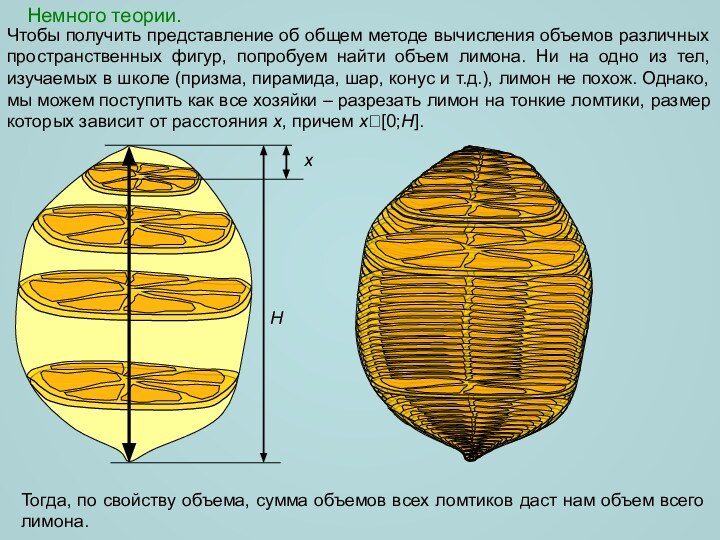
объемов различных пространственных фигур, попробуем найти объем лимона. Ни
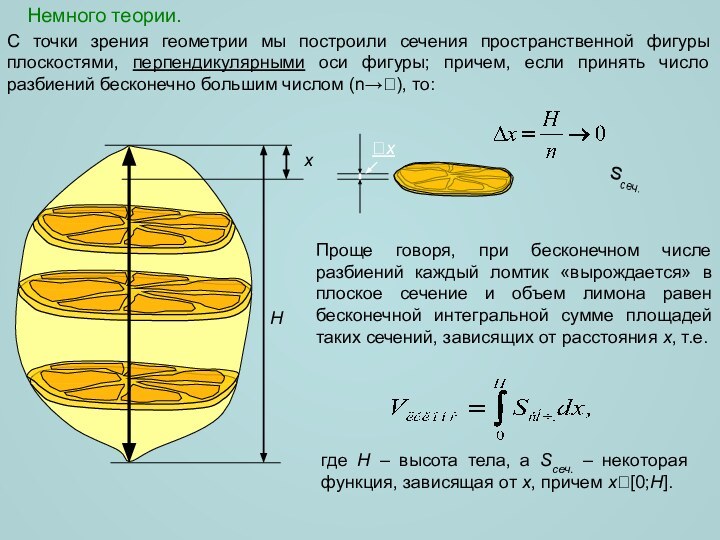
на одно из тел, изучаемых в школе (призма, пирамида, шар, конус и т.д.), лимон не похож. Однако, мы можем поступить как все хозяйки – разрезать лимон на тонкие ломтики, размер которых зависит от расстояния x, причем x[0;H].H
x
Тогда, по свойству объема, сумма объемов всех ломтиков даст нам объем всего лимона.


![Вычисление объемов пространственных тел с помощью интеграла I. Объем прямоугольного параллелепипедас высотой H и площадью основания S.xHx[0;H]0Площадь сечения не](/img/tmb/11/1039236/0e6d1ab259df5792b2d289573fb64dc8-720x.jpg)
![Вычисление объемов пространственных тел с помощью интеграла II. Объем прямой призмыс высотой H и площадью основания S.xx[0;H]H0Площадь сечения не](/img/tmb/11/1039236/e06a4d4449d02f34a901adc8dc762588-720x.jpg)
![Вычисление объемов пространственных тел с помощью интеграла III. Объем n-угольной прямой призмы с высотой H и площадью основания S.xx[0;H]H0Площадь](/img/tmb/11/1039236/c2bd7f492fea86c0ddf11d98793ea4a2-720x.jpg)
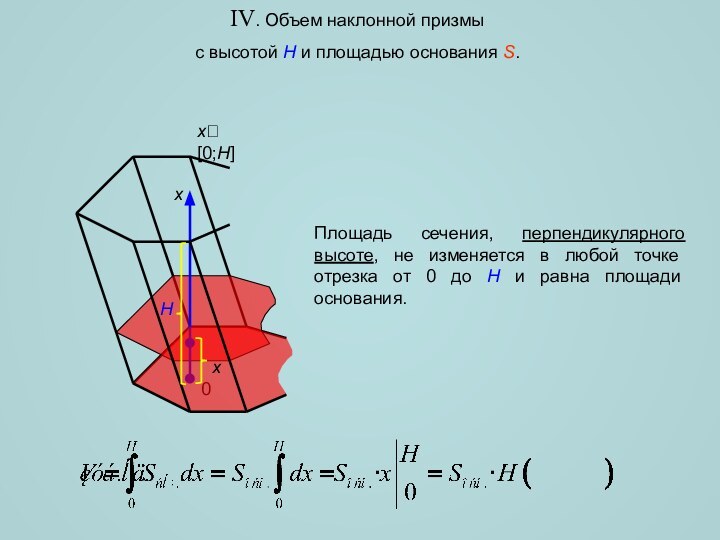
![Вычисление объемов пространственных тел с помощью интеграла V. Объем треугольной пирамидыс высотой H и площадью основания S.Hxx[0;H]⇒xПлощадь сечения изменяется](/img/tmb/11/1039236/1a2706a87917017f409f4fdfb6de0a61-720x.jpg)
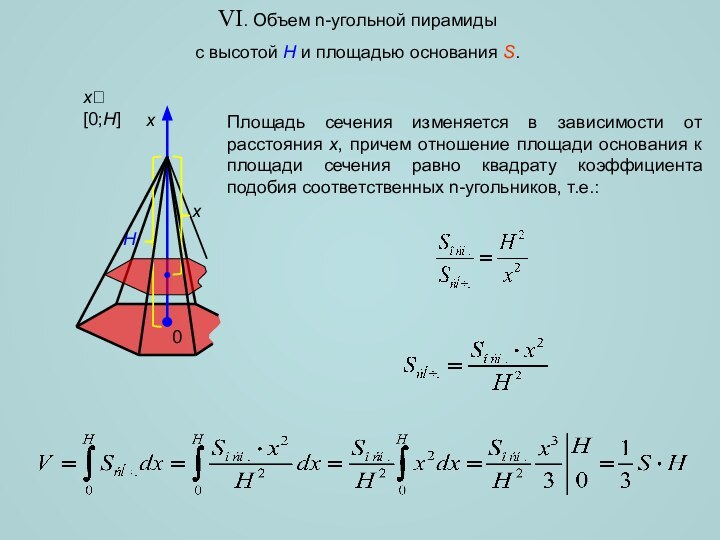

![Вычисление объемов пространственных тел с помощью интеграла VIII. Объем цилиндра с высотой H и площадью основания S.xx[0;H]H0xПлощадь сечения не](/img/tmb/11/1039236/6b0ff935d9a137ea7b841447d1ef5fc4-720x.jpg)
![Вычисление объемов пространственных тел с помощью интеграла IX. Объем конуса с высотой H и площадью основания S.xx[0;H]HxПлощадь сечения изменяется](/img/tmb/11/1039236/86d1e632778e382cbbeb8d2bf7019773-720x.jpg)