x³
y = e
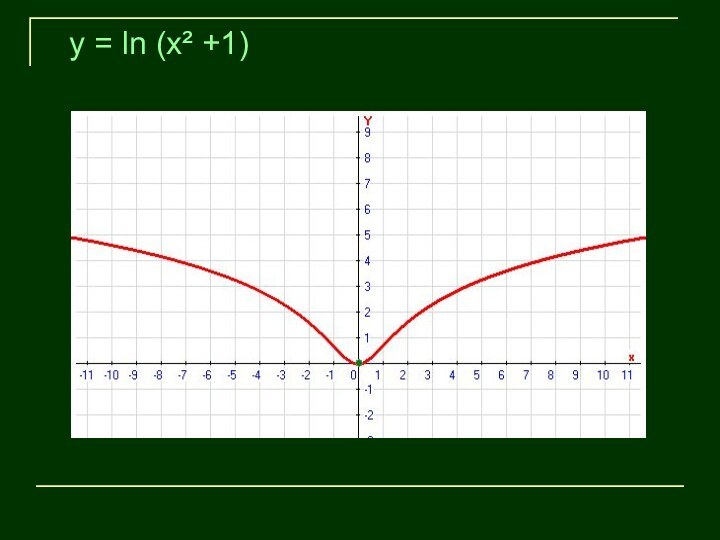
y = ln (x² +1)
Построить график функции
Вариант 2
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
















а b
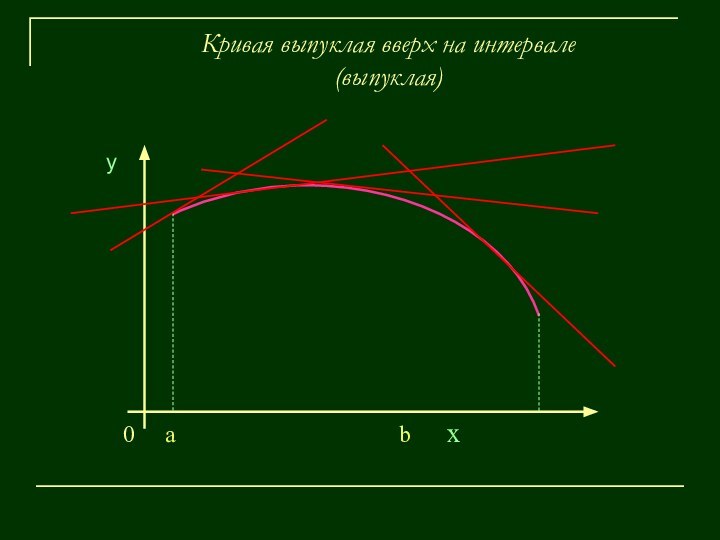
у
а b
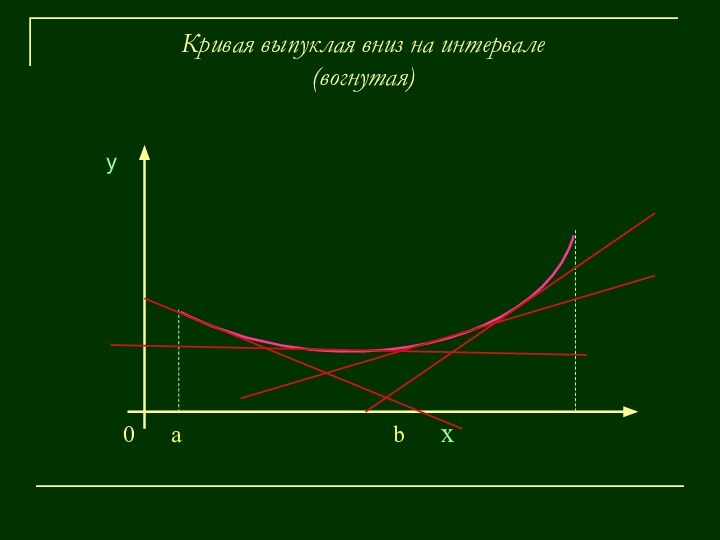
у
у
а х
у
а х
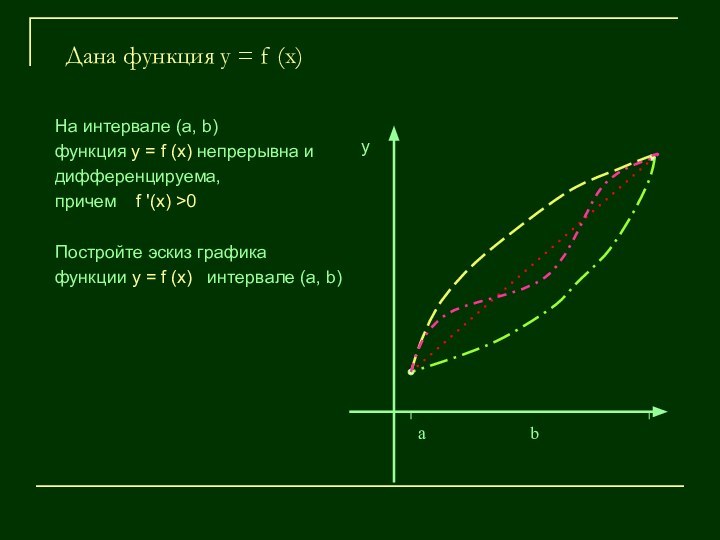
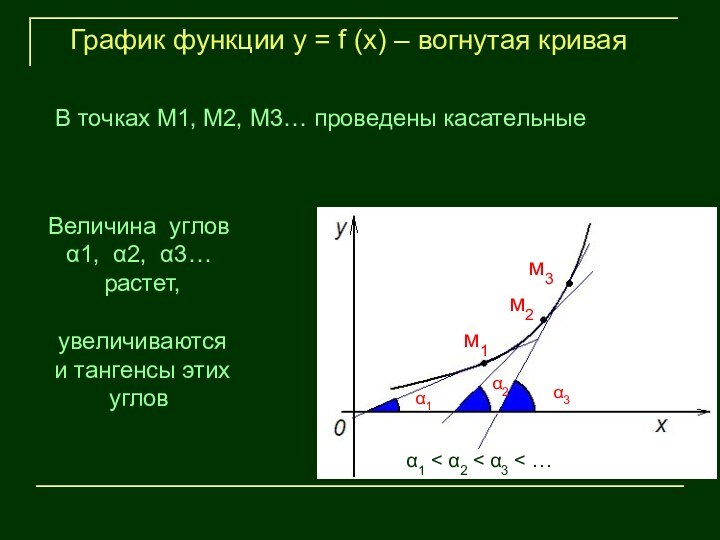
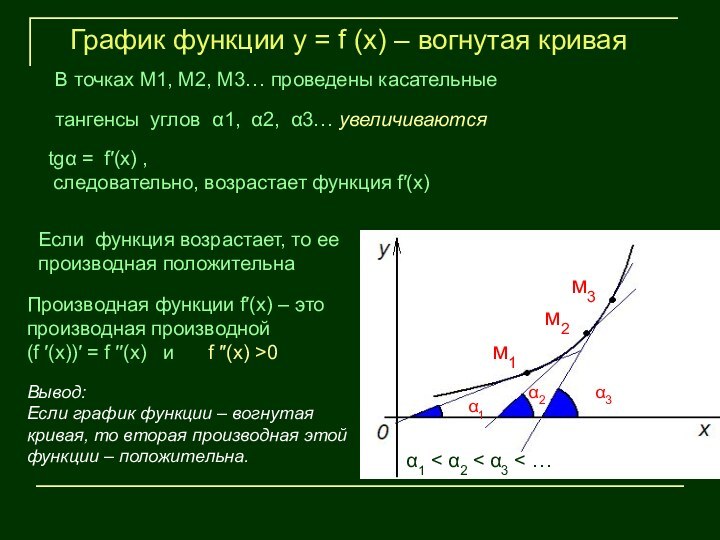
В точках М1, М2, М3… проведены касательные
α1 < α2 < α3 < …
тангенсы углов α1, α2, α3… увеличиваются
tgα = f′(х) ,
следовательно, возрастает функция f′(х)
Если функция возрастает, то ее производная положительна
Производная функции f′(х) – это производная производной
(f ′(х))′ = f ′′(х) и f ′′(х) >0
Вывод:
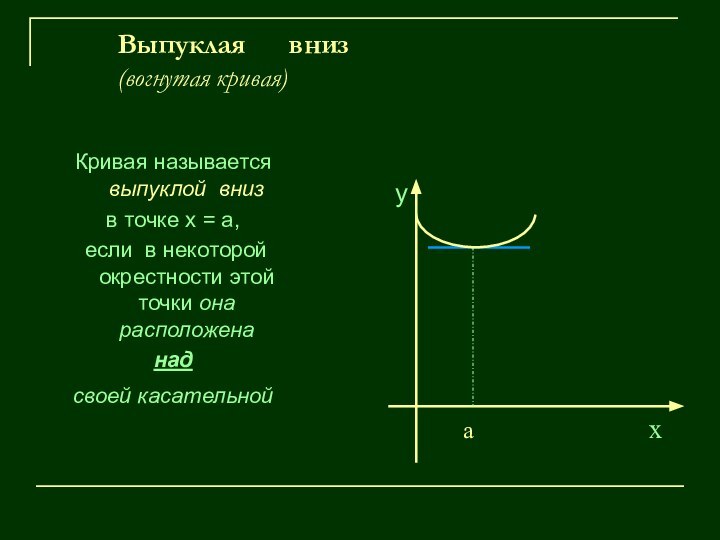
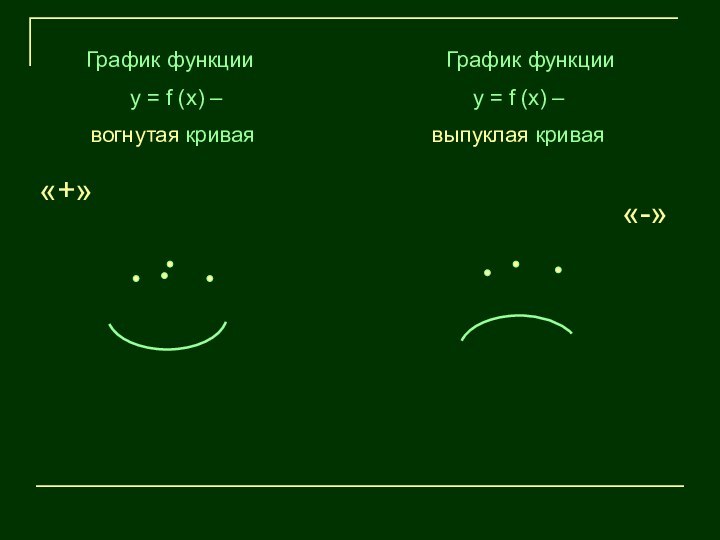
Если график функции – вогнутая кривая, то вторая производная этой функции – положительна.
В точках М1, М2, … проведены касательные
производная функции y = f ′(х)
(f ′(х))′ = f ′′(х) - отрицательна, т.е.
f ′′(х) < 0
м1
м2
α1
α2
α1 > α2 > α3 > …
тангенсы углов α1, α2, α3… убывают
Вывод:
Если график функции – выпуклая кривая, то вторая производная этой функции – отрицательна.
-3 0 2 5 f
х = -3, х = 0, х = 2 х = 5 – точки перегиба
+ - + - + f‘‘
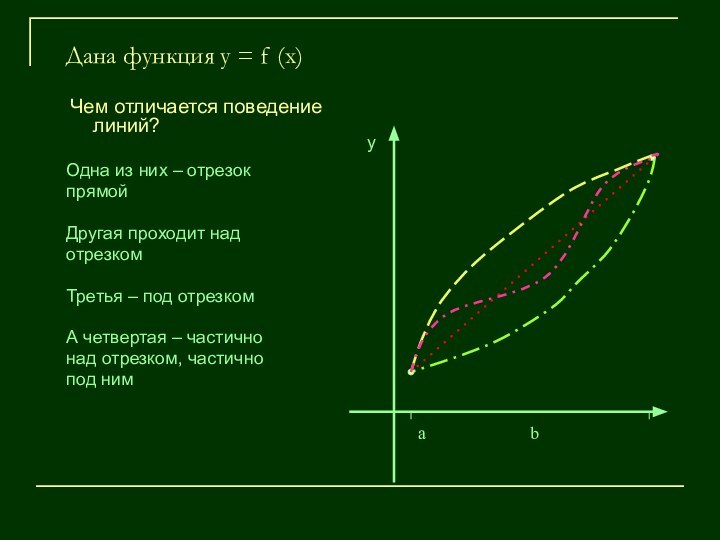
«+»
«-»
Интервалы выпуклости:
(-∞, 0)
Интервалы вогнутости:
(0, +∞)
- + f ‘‘
0 f
х = 0 – точка перегиба
Интервалы выпуклости:
(-1, 1)
Интервалы вогнутости:
(-∞, -1) и (1, +∞)
+ - + f‘‘
-1 1 f
х = 1 и х = -1 – точки перегиба