- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Выпуклые четырёхугольники. Специфика параллелограммов. Специфика трапеций
Содержание
- 2. Площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними:
- 4. Середины сторон выпуклого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади данного четырёхугольника.
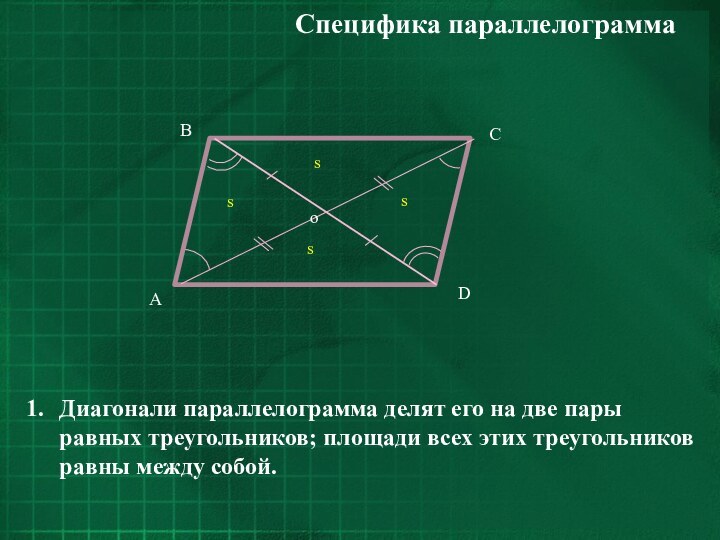
- 5. Диагонали параллелограмма делят его на две пары
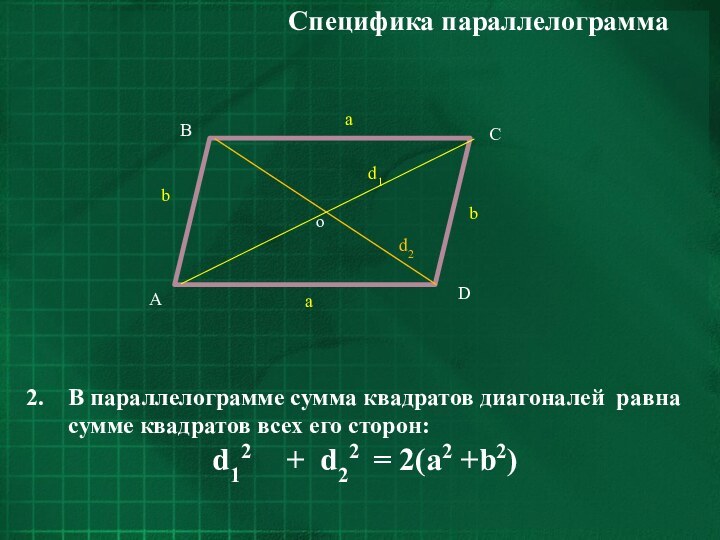
- 6. В параллелограмме сумма квадратов диагоналей равна сумме
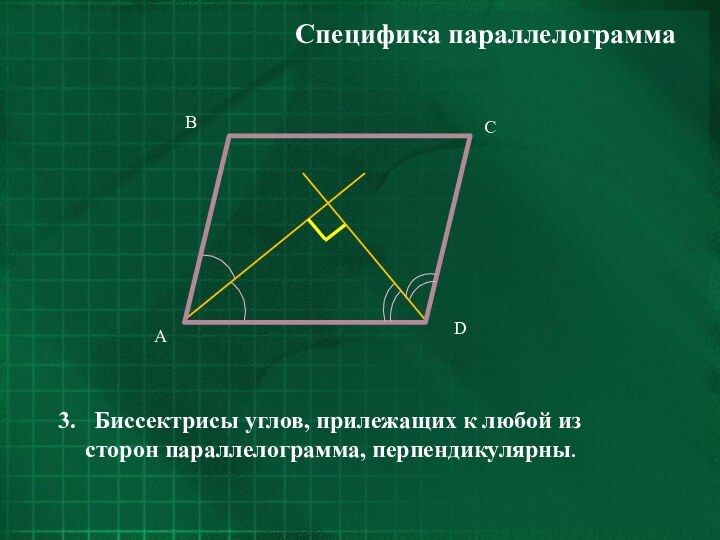
- 7. Специфика параллелограмма3. Биссектрисы углов, прилежащих к любой из сторон параллелограмма, перпендикулярны.
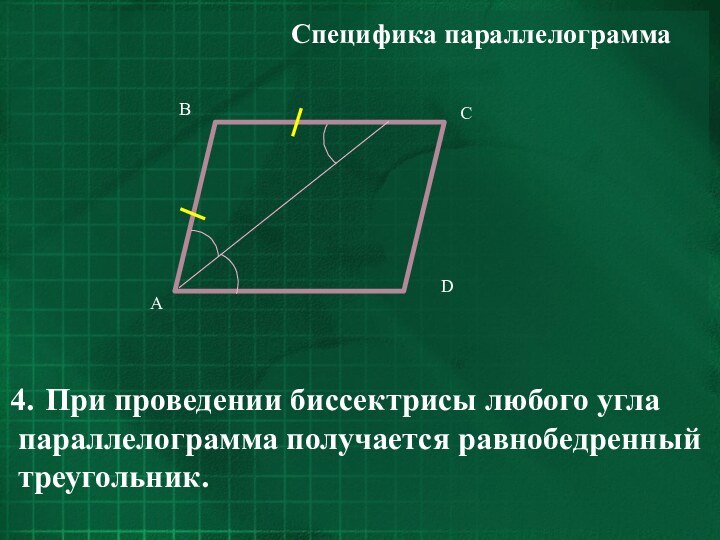
- 8. Специфика параллелограммаПри проведении биссектрисы любого углапараллелограмма получается равнобедренныйтреугольник.
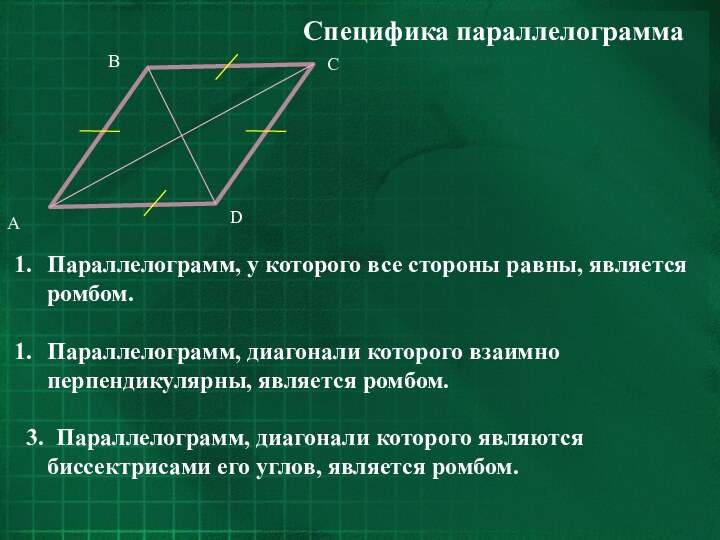
- 9. Специфика параллелограммаПараллелограмм, у которого все стороны равны,
- 10. Специфика параллелограмма5. Параллелограмм, диагонали которого равны, является
- 11. Специфика трапецийДиагонали трапеции, пересекаясь, образуют четыре треугольника,
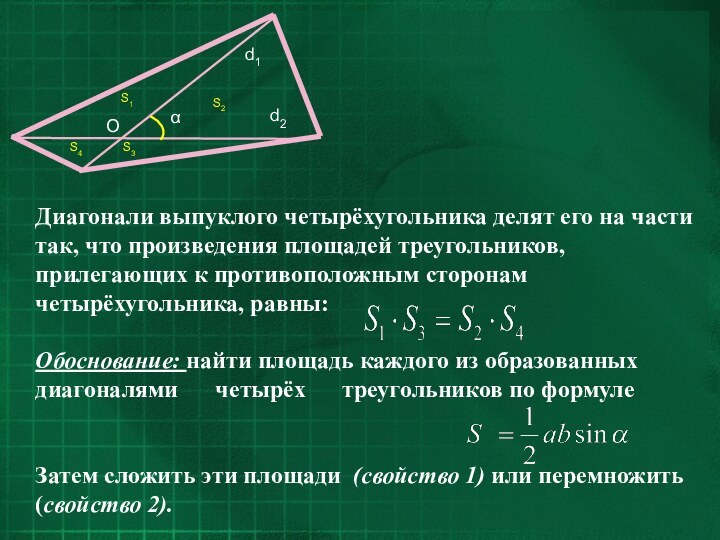
- 12. Специфика трапеций2. SBAD = SCAD, SABC
- 13. Специфика трапеций5. Диагонали трапеции делят её на
- 14. 6. Биссектрисы углов, прилежащих к боковым
- 15. Специфика трапецийОсновные (наиболее распространённые) дополнительные построения в
- 16. Специфика трапецийОсновные (наиболее распространённые) дополнительные построения в
- 17. Специфика трапецийОсновные (наиболее распространённые) дополнительные построения в
- 18. Задача №1. (Тренировочные варианты Иркутск 2013г.)Найдите площадь
- 19. Решение.Точки K, Р, Т, Н середины
- 20. Задача №2. (ФИПИ 2014г.)На стороне ВC параллелограмма
- 21. Решение.△AВD = △CDB (по трём равным сторонам).
- 22. 5. Из п.3 и п.1 SAВP =
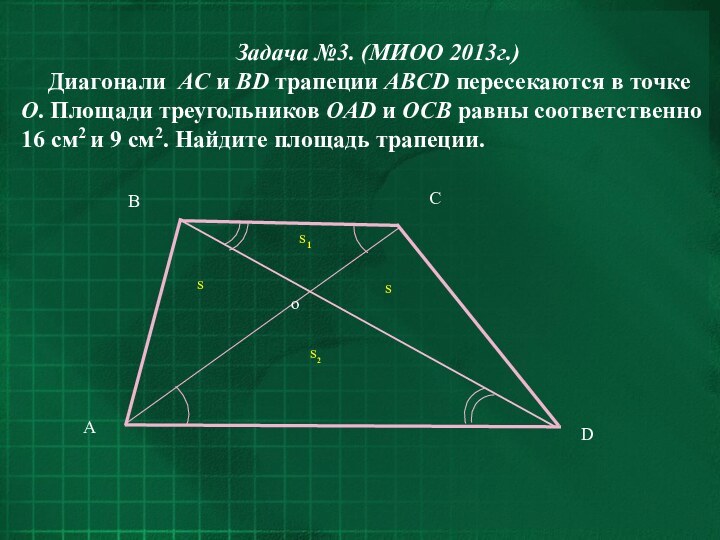
- 23. Задача №3. (МИОО 2013г.)Диагонали AC и BD
- 24. Решение.По условию SOAD не равна SOCB ,
- 25. 4. SBAD = SCAD , т. к.
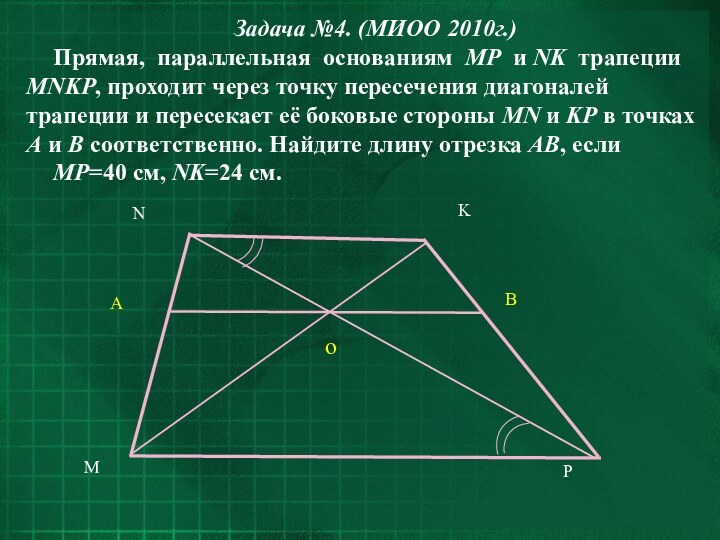
- 26. Задача №4. (МИОО 2010г.)Прямая, параллельная основаниям MP
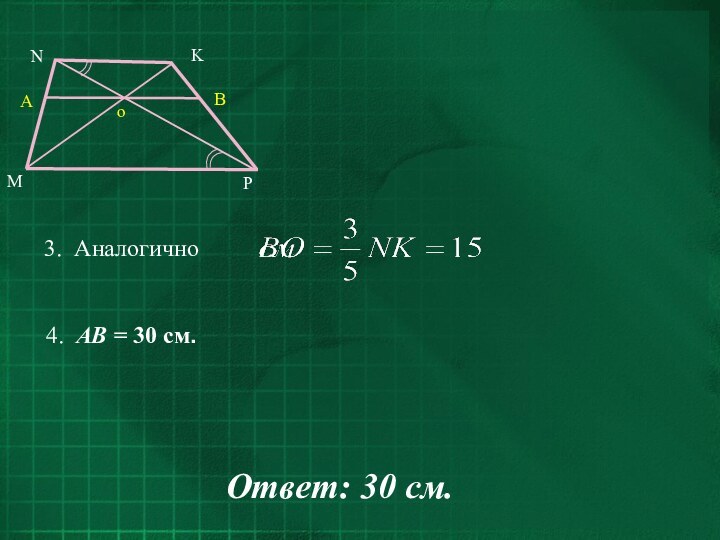
- 28. 4. AB = 30 см. Ответ: 30 см.
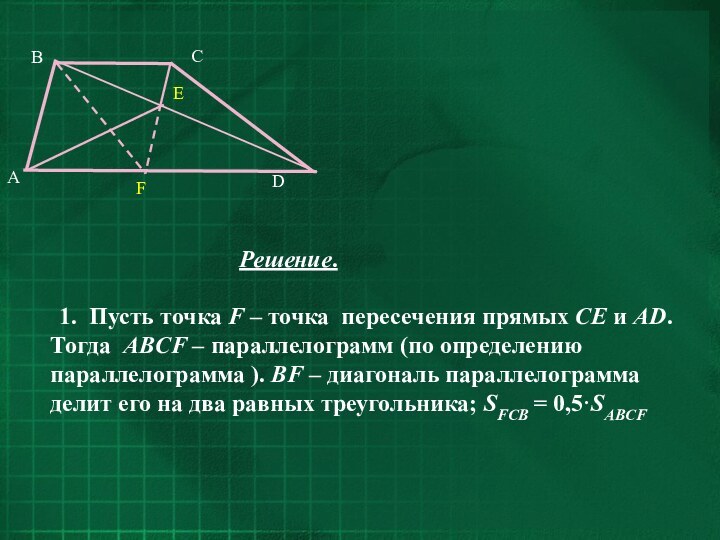
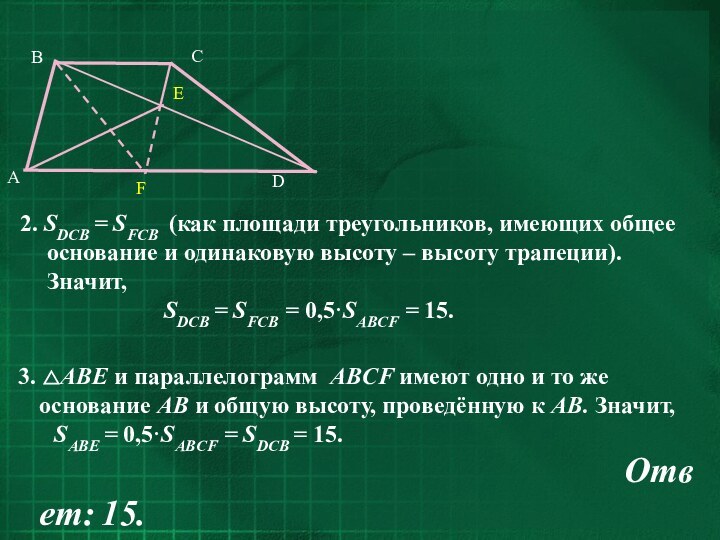
- 30. Решение. 1. Пусть точка F
- 31. 3. △AВE и параллелограмм ABCF имеют
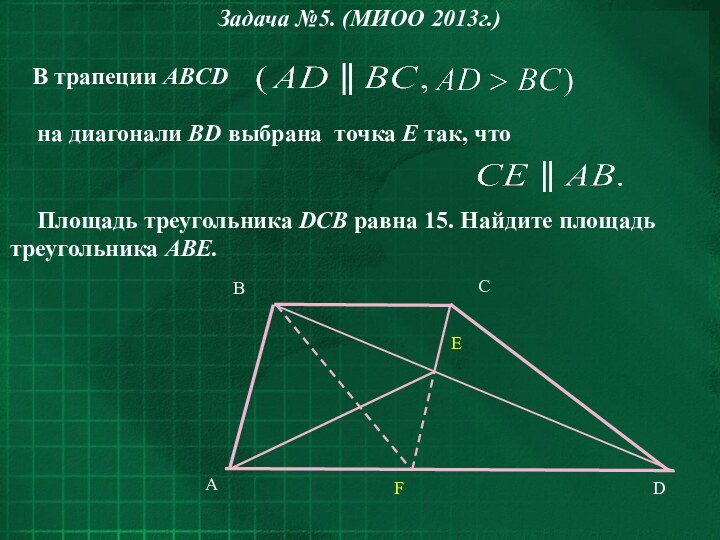
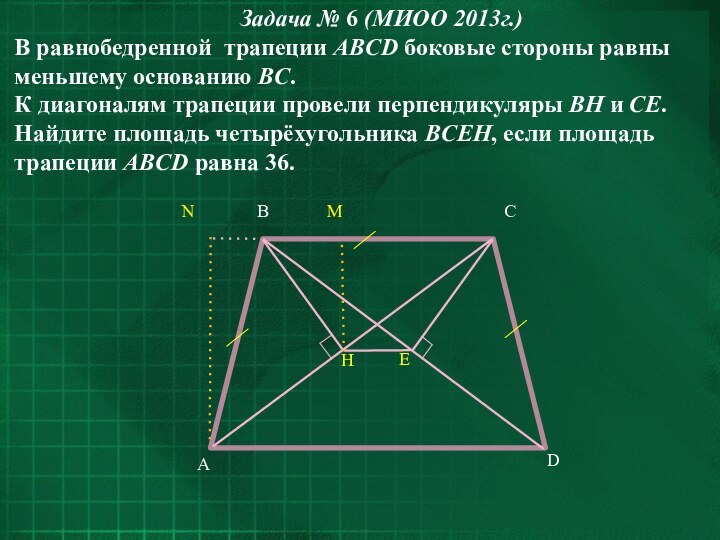
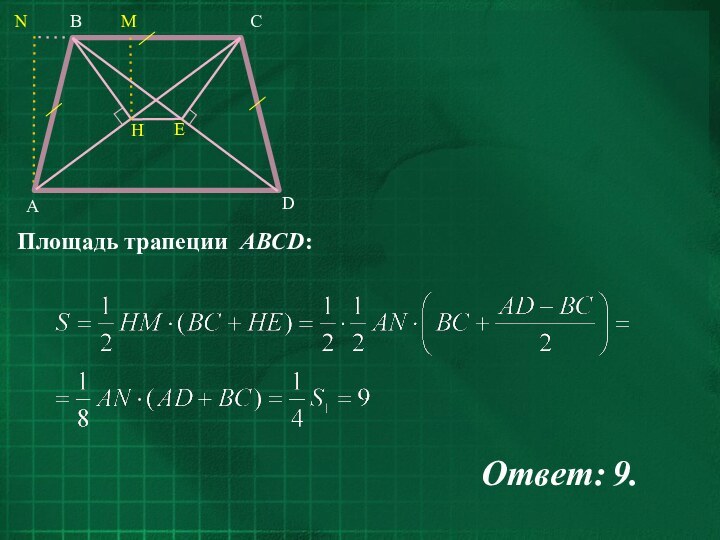
- 32. Задача № 6 (МИОО 2013г.)В равнобедренной трапеции ABCD боковые
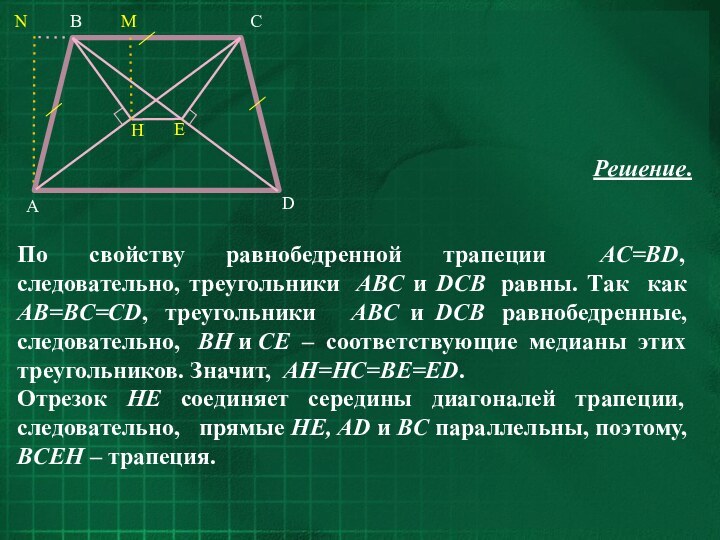
- 33. Решение.По свойству равнобедренной трапеции AC=BD, следовательно, треугольники
- 34. Ответ: 9.
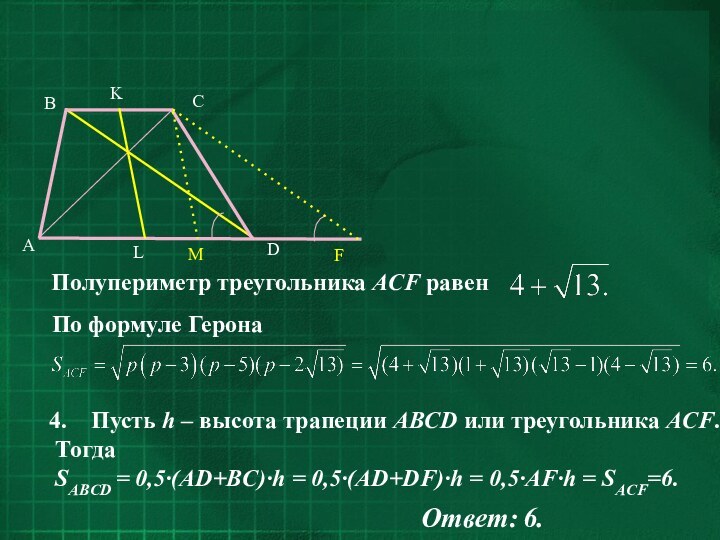
- 35. Задача № 7.Диагонали трапеции 3 и 5;
- 36. Пусть h – высота трапеции ABCD или
- 37. 1. Найдите площадь выпуклого четырёхугольника с диагоналями
- 38. 4. Диагонали AC и BD трапеции ABCD
- 39. Скачать презентацию
- 40. Похожие презентации

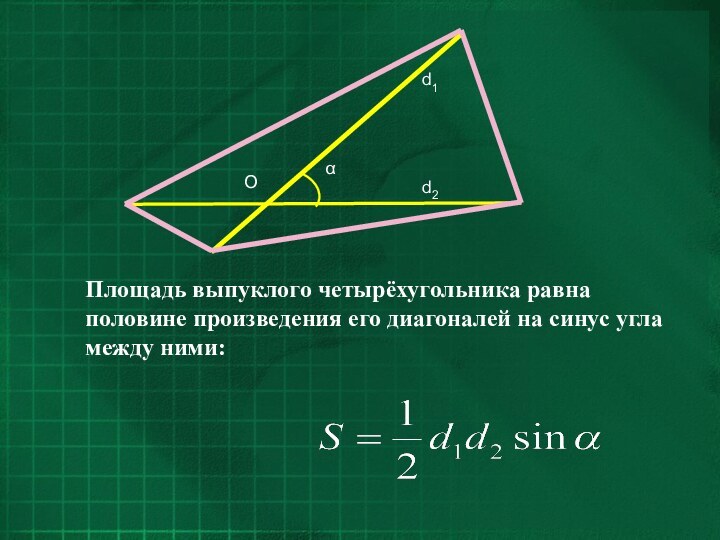













Слайд 2 Площадь выпуклого четырёхугольника равна половине произведения его диагоналей
на синус угла между ними:
Слайд 4 Середины сторон выпуклого четырёхугольника являются вершинами параллелограмма, площадь
которого равна половине площади данного четырёхугольника.
Слайд 5
Диагонали параллелограмма делят его на две пары равных
треугольников; площади всех этих треугольников равны между собой.
Специфика параллелограмма
Слайд 6
В параллелограмме сумма квадратов диагоналей равна сумме квадратов
всех его cторон:
d12 + d22 =
2(a2 +b2)Специфика параллелограмма
Слайд 7
Специфика параллелограмма
3. Биссектрисы углов, прилежащих к любой
из сторон параллелограмма, перпендикулярны.
Слайд 8
Специфика параллелограмма
При проведении биссектрисы любого угла
параллелограмма получается равнобедренный
треугольник.
Слайд 9
Специфика параллелограмма
Параллелограмм, у которого все стороны равны, является
ромбом.
Параллелограмм, диагонали которого взаимно перпендикулярны, является ромбом.
3. Параллелограмм,
диагонали которого являются биссектрисами его углов, является ромбом.
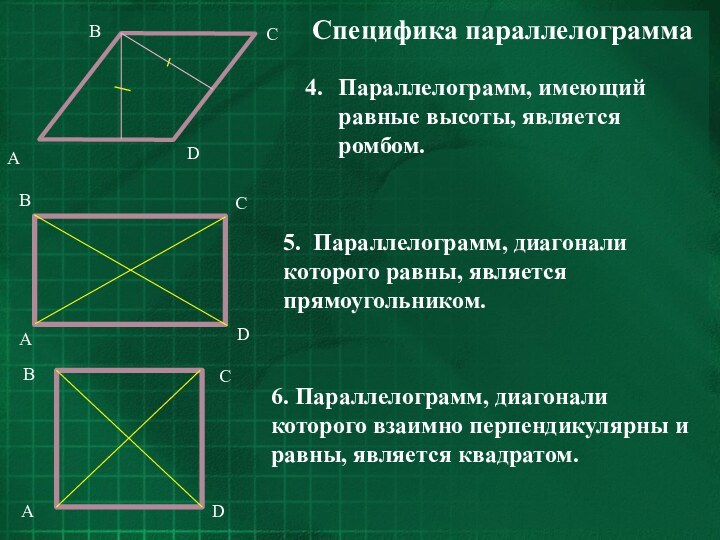
Слайд 10
Специфика параллелограмма
5. Параллелограмм, диагонали которого равны, является прямоугольником.
6.
Параллелограмм, диагонали которого взаимно перпендикулярны и равны, является квадратом.
Параллелограмм,
имеющий равные высоты, является ромбом.
Слайд 11
Специфика трапеций
Диагонали трапеции, пересекаясь, образуют
четыре треугольника, два
из которых
равновелики, а два других – подобны с
коэффициентом подобия
равным отношениюоснований трапеции.
△OAD~ △OCB (по двум равным углам),
SOAD : SOCB = k2, где k = AD:BC = OA:OC = OD:OB.
Слайд 12
Специфика трапеций
2. SBAD = SCAD, SABC =
SDBC (как площади треугольников, имеющих cоответственно одинаковые основания и
высоты).3. SOAB = SOCD (т.к. SOAB = SABC – SOBC = SDBC – SOBC= SOCD).
4. SBAD : SDBC = AD : BC (SBAD = 0,5·AD·h, SDBC = 0,5·BC·h).
Слайд 13
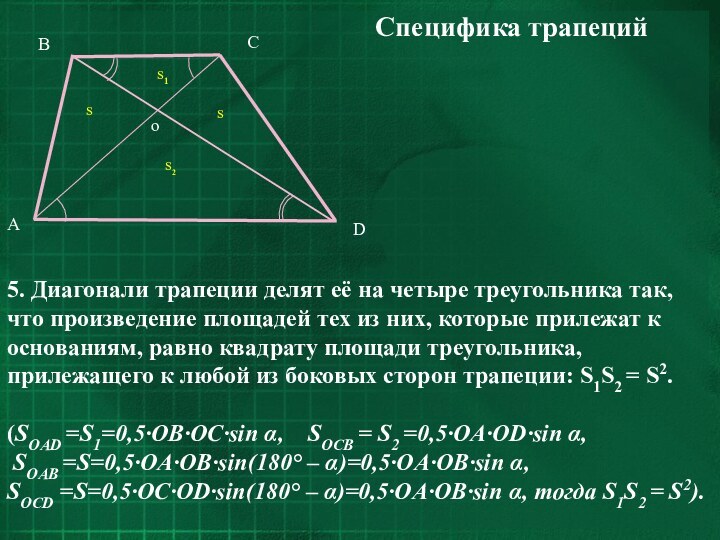
Специфика трапеций
5. Диагонали трапеции делят её на четыре
треугольника так, что произведение площадей тех из них, которые
прилежат к основаниям, равно квадрату площади треугольника, прилежащего к любой из боковых сторон трапеции: S1S2 = S2.(SOAD =S1=0,5·OB·OC·sin α, SOCB = S2 =0,5·OA·OD·sin α,
SOAB =S=0,5·OA·OB·sin(180° – α)=0,5·OA·OB·sin α,
SOCD =S=0,5·OC·OD·sin(180° – α)=0,5·OA·OB·sin α, тогда S1S2 = S2).
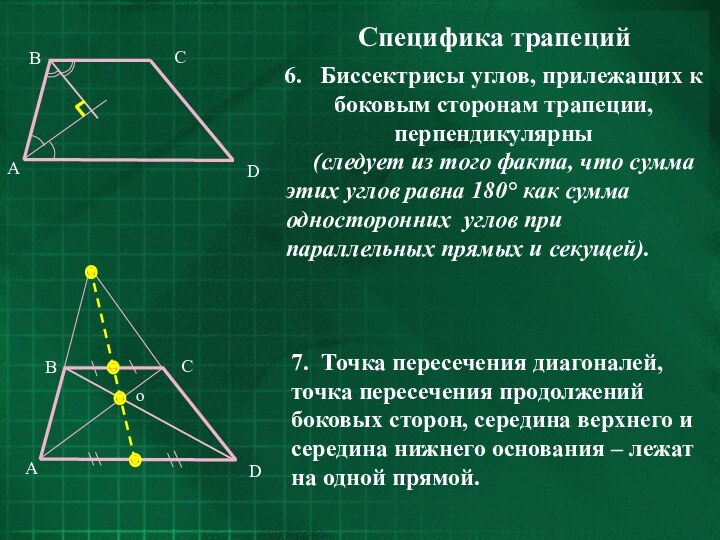
Слайд 14 6. Биссектрисы углов, прилежащих к боковым сторонам
трапеции, перпендикулярны
(следует из того факта, что сумма этих углов
равна 180° как сумма односторонних углов при параллельных прямых и секущей).7. Точка пересечения диагоналей, точка пересечения продолжений боковых сторон, середина верхнего и середина нижнего основания – лежат на одной прямой.
Специфика трапеций
Слайд 15
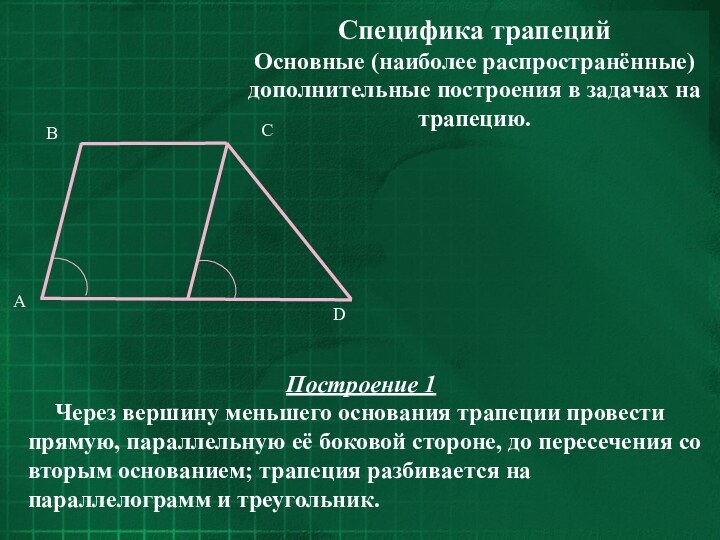
Специфика трапеций
Основные (наиболее распространённые) дополнительные построения в задачах
на трапецию.
Построение 1
Через вершину меньшего основания трапеции провести
прямую, параллельную её боковой стороне, до пересечения со вторым основанием; трапеция разбивается на параллелограмм и треугольник.
Слайд 16
Специфика трапеций
Основные (наиболее распространённые) дополнительные построения в задачах
на трапецию
Построение 2
Из вершины С меньшего основания трапеции
ABCD провести прямую CE, параллельную диагонали BD, до пересечения с AD в точке E; получится треугольник ACE, две стороны которого равны диагоналям трапеции, а длина третьей равна сумме длин оснований трапеции AE = AD + DE.
При этом площадь трапеции ABCD равна площади образованного треугольника ACE: SABCD = SACE
Слайд 17
Специфика трапеций
Основные (наиболее распространённые) дополнительные построения в задачах
на трапецию
Построение 4
Достроить трапецию ABCD до треугольника APD,
вершина Р которого образуется при пересечении продолжений боковых сторон трапеции.
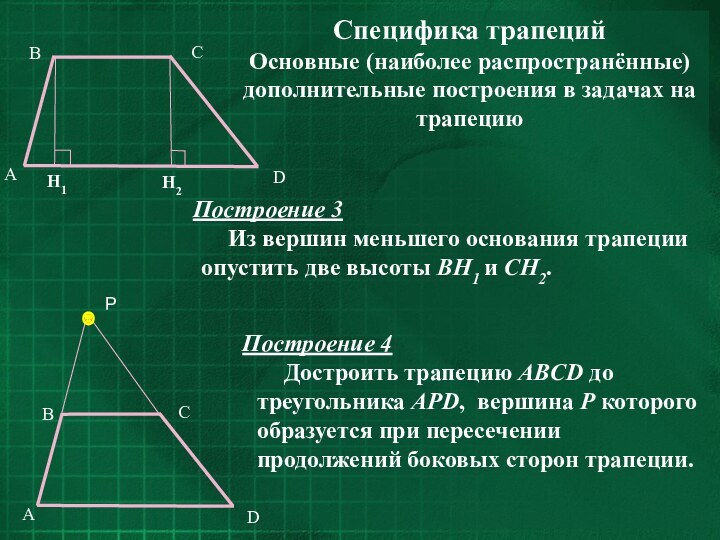
Построение 3
Из вершин меньшего основания трапеции опустить две высоты BH1 и CH2.
Слайд 18
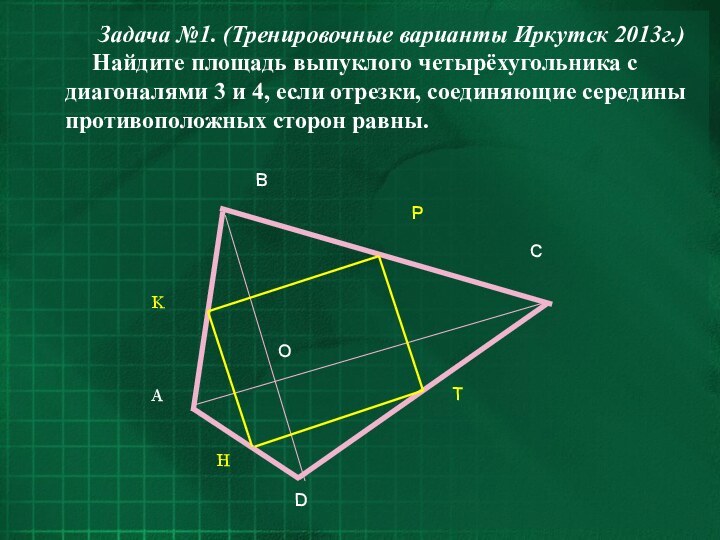
Задача №1. (Тренировочные варианты Иркутск 2013г.)
Найдите площадь выпуклого
четырёхугольника с диагоналями 3 и 4, если отрезки, соединяющие
середины противоположных сторон равны.
Слайд 19
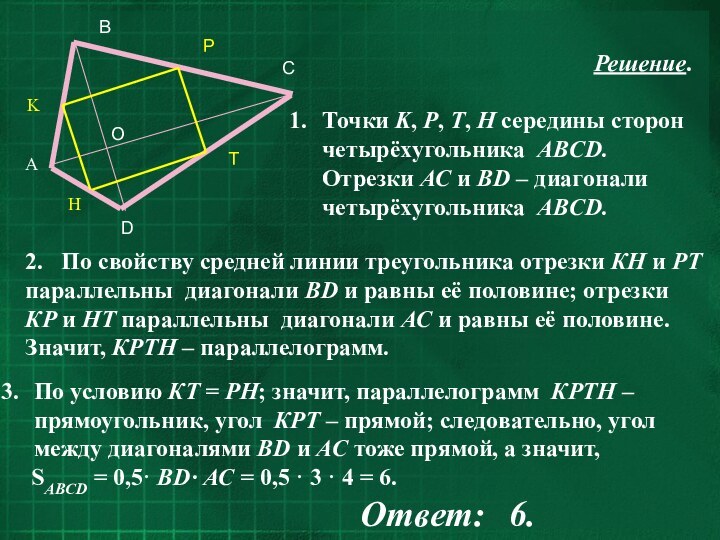
Решение.
Точки K, Р, Т, Н середины сторон
четырёхугольника ABCD. Отрезки АС и ВD – диагонали четырёхугольника
ABCD.По условию КТ = РН; значит, параллелограмм КРТН – прямоугольник, угол КРТ – прямой; следовательно, угол между диагоналями ВD и АС тоже прямой, а значит,
SABCD = 0,5· ВD· АС = 0,5 · 3 · 4 = 6.
Ответ: 6.
2. По свойству средней линии треугольника отрезки КН и РТ параллельны диагонали ВD и равны её половине; отрезки КР и НТ параллельны диагонали АС и равны её половине. Значит, КРТН – параллелограмм.
Слайд 20
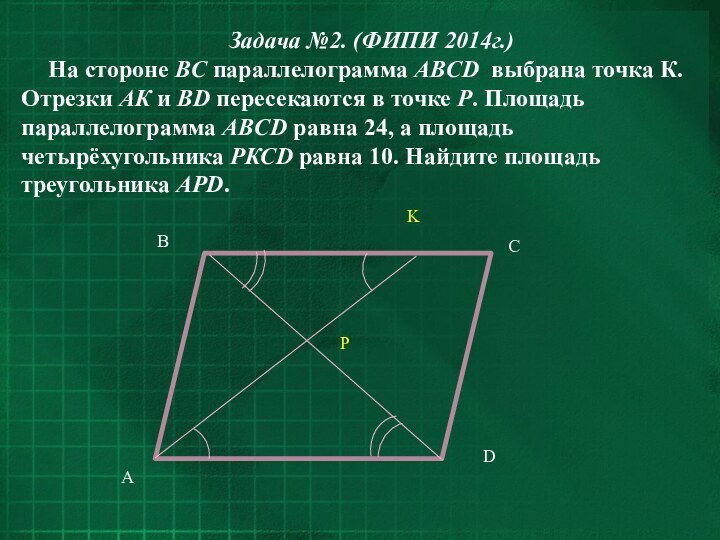
Задача №2. (ФИПИ 2014г.)
На стороне ВC параллелограмма ABCD
выбрана точка К. Отрезки АК и ВD пересекаются в
точке Р. Площадь параллелограмма ABCD равна 24, а площадь четырёхугольника РКСD равна 10. Найдите площадь треугольника АРD.
Слайд 21
Решение.
△AВD = △CDB (по трём равным сторонам).
SAВD
= SCDB = 0,5·SAВCD = =0,5·24=12;
SКРB = SCDB – SPKCD = 12 – 10 = 22. △APD~ △KPB (по двум равным углам); SAРD : SKPB = k2; AP=k·PK, DP=k·PB
3. △AВP и △ВPK имеют общую высоту из вершины В, значит, отношение их площадей равно отношению их оснований, т.е. SAВP : SKPB = АP : PK = k (из п.2)
4. △APD и △ABP имеют общую высоту из вершины A, значит, отношение их площадей равно отношению их оснований, т.е. SAP D : SAВP = DP : PB = k (из п.2)
Слайд 22 5. Из п.3 и п.1 SAВP = k·SKPB
= 2k
6. Из п.4 и п.5
SAPD = k·SABP
= k·2k = 2k2 SABD = SAВP + SAPD = 2k + 2k2 .
Из п.1 следует 2k + 2k2 = 12.
Корни уравнения k2 + k – 6 = 0 числа –3 и 2;
по смыслу задачи k = 2.
8. SAPD = 2k2 = 2·22 = 8.
Ответ: 8.
Слайд 23
Задача №3. (МИОО 2013г.)
Диагонали AC и BD трапеции
ABCD пересекаются в точке О. Площади треугольников OАD и
OCВ равны соответственно 16 см2 и 9 см2. Найдите площадь трапеции.
Слайд 24
Решение.
По условию SOAD не равна SOCB , значит,
AD и BC – основания трапеции ABCD.
2.
△OAD~ △OCB (по двум равным углам), SOAD : SOCB = k2 =16:9, где k = 4:3 = OA:OC.Слайд 25 4. SBAD = SCAD , т. к.
эти треугольники имеют общее основание AD и их высоты,
проведённые к этому основанию, равны как высоты трапеции. Значит,SOAB = SABC – SOBC = SDBC – SOBC= SOCD , т. е. SOCD = SOAB = 12.
5. SAВCD = SOAD + SOCB + SOCD + SOAB =16 + 9 + 12 +12 = 49 cм2.
Ответ: 49 cм2.
Слайд 26
Задача №4. (МИОО 2010г.)
Прямая, параллельная основаниям MP и
NK трапеции MNKP, проходит через точку пересечения диагоналей трапеции
и пересекает её боковые стороны MN и KP в точках A и B соответственно. Найдите длину отрезка AB, еслиMP=40 см, NK=24 см.
Слайд 30
Решение.
1. Пусть точка F –
точка пересечения прямых CE и AD. Тогда ABCF –
параллелограмм (по определению параллелограмма ). BF – диагональ параллелограмма делит его на два равных треугольника; SFCB = 0,5·SABCF
Слайд 31 3. △AВE и параллелограмм ABCF имеют одно
и то же основание AB и общую высоту, проведённую
к AB. Значит,SАВЕ = 0,5·SABCF = SDCB = 15.
Ответ: 15.
2. SDCB = SFCB (как площади треугольников, имеющих общее основание и одинаковую высоту – высоту трапеции). Значит,
SDCB = SFCB = 0,5·SABCF = 15.
Слайд 32
Задача № 6 (МИОО 2013г.)
В равнобедренной трапеции ABCD боковые стороны
равны меньшему основанию BC.
К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь
четырёхугольника BCEH, если площадь трапеции ABCD равна 36.
Слайд 33
Решение.
По свойству равнобедренной трапеции AC=BD, следовательно, треугольники ABC
и DCB равны. Так как AB=BC=CD, треугольники ABC
и DCB равнобедренные, следовательно, BH и CE – соответствующие медианы этих треугольников. Значит, AH=HC=BE=ED.Отрезок HE соединяет середины диагоналей трапеции, cледовательно, прямые HE, AD и BC параллельны, поэтому, BCEH – трапеция.
Слайд 35
Задача № 7.
Диагонали трапеции 3 и 5; отрезок,
соединяющий середины оснований 2. Найдите площадь трапеции.
Решение. 1.
Дополнительное построение: СМ параллельна KL, CF параллельна BD.2. Из построения следует: LKCM и DBCF параллелограммы; LM = KC = 0,5·BC, DF= BC, AM = AL+LM = 0,5· AD + 0,5·BC.
3. CM – медиана треугольника ACF. По формуле медианы
Слайд 36
Пусть h – высота трапеции ABCD или треугольника
ACF.
Тогда
SABCD = 0,5·(AD+BC)·h = 0,5·(AD+DF)·h = 0,5·AF·h = SACF=6.
Ответ:
6.Полупериметр треугольника ACF равен
Слайд 37 1. Найдите площадь выпуклого четырёхугольника с диагоналями 8
и 5, если отрезки, соединяющие середины противоположных сторон равны.
2. В выпуклом четырёхугольнике ABCТ длина отрезка, соединяющего середины сторон AB и CТ, равна одному метру. Прямые BТ и AC перпендикулярны. Найдите длину отрезка, соединяющего середины диагоналей AC и BТ. 3. На стороне ВC параллелограмма ABCD выбрана точка К. Отрезки АК и ВD пересекаются в точке Р. Площадь параллелограмма ABCD равна 80, а площадь четырёхугольника РКСD равна 31. Найдите площадь треугольника АРD.Задачи для самостоятельного решения
Слайд 38 4. Диагонали AC и BD трапеции ABCD пересекаются
в точке О. Площади треугольников АOD и ВOC равны
соответственно 25 см2 и 16 см2. Найдите площадь трапеции. 5. Прямая, параллельная основаниям BC и AD трапеции ABCD, проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны AB и CD в точках Е и F соответственно. Найдите длину отрезка ЕF , если AD= =12 см, ВC=24 см. 6. В трапеции ABCD (AD параллельна BC, AD > BC) на диагонали AC выбрана точка Е так, что ВЕ параллельна CD. Площадь треугольника АВC равна 10. Найдите площадь треугольника DЕC.Задачи для самостоятельного решения