}
E(f)={ }
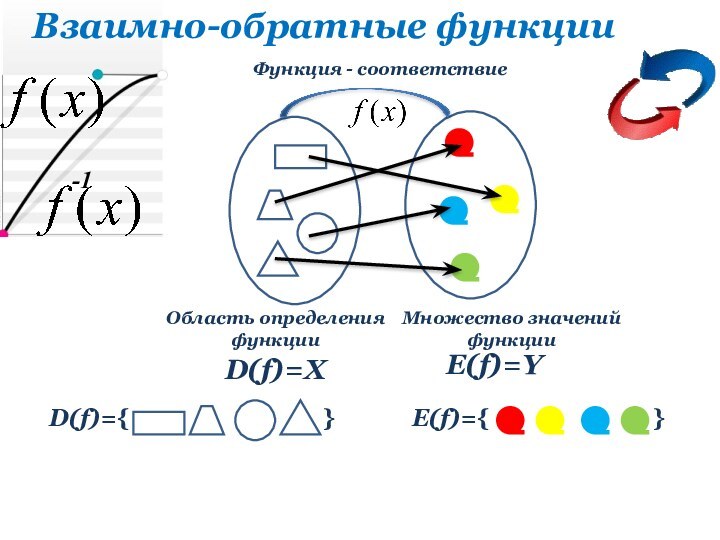
D(f)=X
E(f)=Y
Область определения
функции
Множество значений
функции
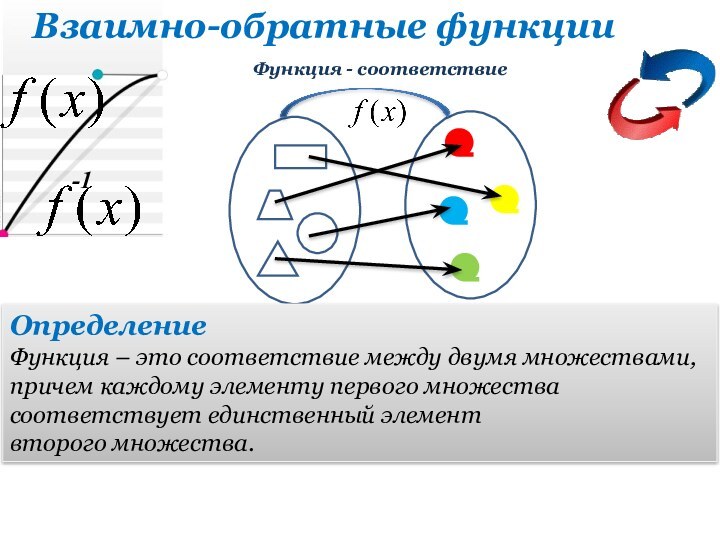
Функция - соответствие
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



E(f)={ }
D(f)=X
E(f)=Y
Область определения
функции
Множество значений
функции
Функция - соответствие
E(f)={ }
D(f)=X
E(f)=Y
Область определения
функции
Множество значений
функции
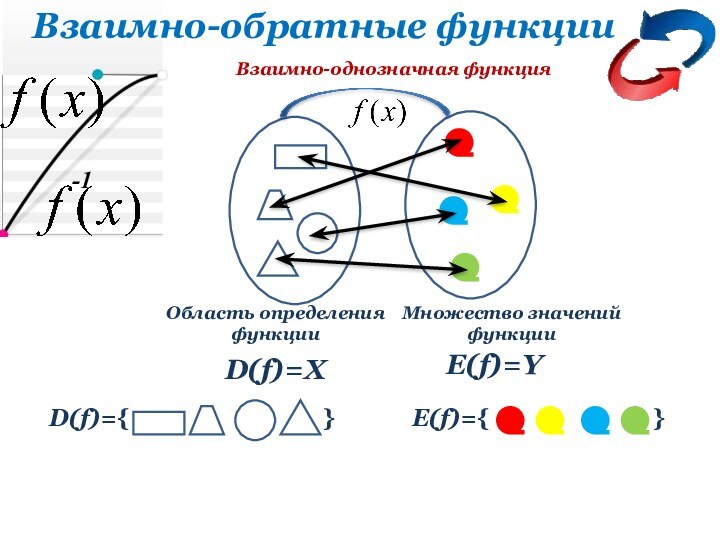
Взаимно-однозначная функция
E(f)={ }
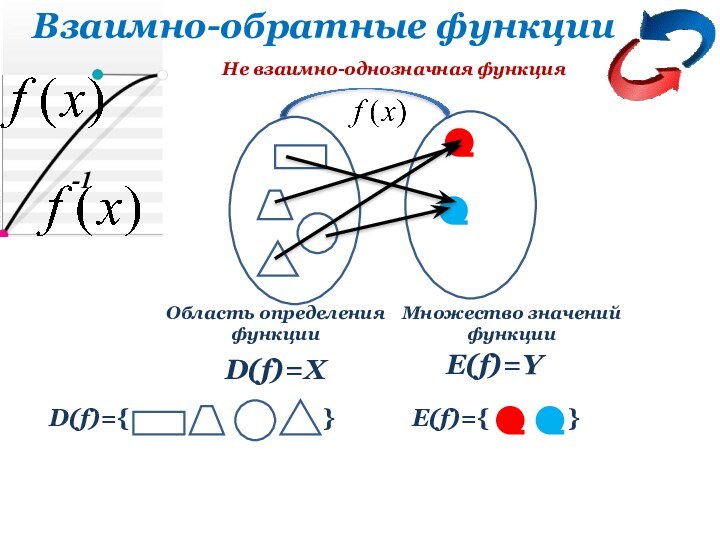
D(f)=X
E(f)=Y
Область определения
функции
Множество значений
функции
Не взаимно-однозначная функция
E(f )={ }
D(f )=Y
E(f )=X
Область определения
обратной функции
Множество значений
обратной функции
Обратная функция
-1
-1
-1
-1
Определение
Функция f называется обратимой, если для любых двух различных чисел х1 и x2, принадлежащих D(f), числа f(x1) и f(x2) также различны.