Слайд 2
Взаимное пересечение поверхностей
1. Линия пересечения поверхностей в общем
случае пространственная кривая, множество точек которой принадлежит обеим поверхностям.
2. Точка принадлежит поверхности, если она принадлежит линии данной поверхности.
3. Чтобы точка принадлежала обеим заданным поверхностям, она должна быть точкой пересечения линий, принадлежащих поверхностям.
4. Линии пересекаются, если они принадлежат одной плоскости или поверхности.
Слайд 3
Взаимное пересечение поверхностей
Для определения общей точки двух поверхностей
(Ω и Φ), необходимо ввести вспомогательную поверхность (Δ), пересекающую
заданные поверхности по графически простым линиям (прямым и окружностям), которые проецируются также в виде графически простых линий.
Слайд 4
Взаимное пересечение поверхностей
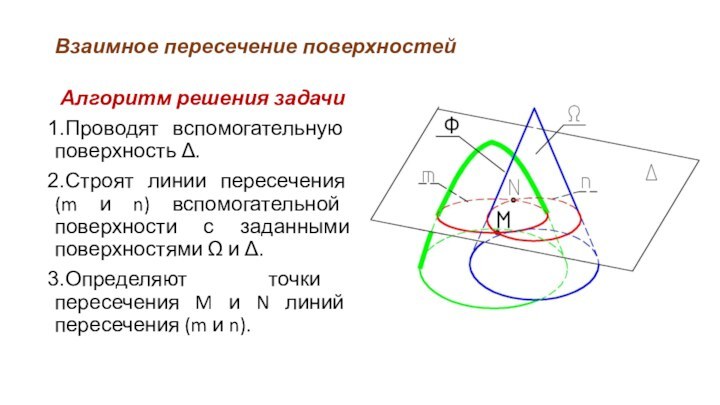
Алгоритм решения задачи
Проводят вспомогательную поверхность Δ.
Строят
линии пересечения (m и n) вспомогательной поверхности с заданными
поверхностями Ω и Δ.
Определяют точки пересечения M и N линий пересечения (m и n).
Слайд 5
Взаимное пересечение поверхностей
Порядок построения точек :
Экстремальные точки (высшая,
низшая, крайние левая и правая, ближайшая и наиболее удаленная).
Очерковые,
лежащие на линиях видимости.
Промежуточные или случайные.
Первые две группы точек обозначают на чертеже буквами, третью – цифрами.
Полученные точки соединяют плавной линией с учетом видимости поверхностей.
Слайд 6
Взаимное пересечение поверхностей
В качестве вспомогательных секущих поверхностей используют
плоскости (частного и общего положения) и сферы.
Выбор посредника зависит
от вида пересекающихся поверхностей, их взаимного положения, их положения относительно плоскостей проекций, поэтому решение задачи начинают с анализа вида и положения поверхностей.
Слайд 7
Взаимное пересечение поверхностей
Основные способы решения задач
на взаимное
пересечение поверхностей
Способ вспомогательных секущих плоскостей (частного и общего положения).
Способ
вспомогательных сфер (концентрических и эксцентрических)
Слайд 8
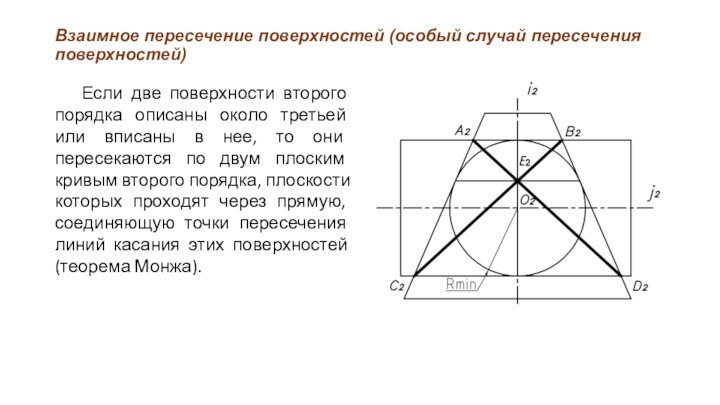
Взаимное пересечение поверхностей (способ вспомогательных секущих плоскостей)
Способ вспомогательных
секущих плоскостей применяют, если можно подобрать плоскость, пересекающую обе
поверхности по графически простым линиям.
Чаще всего в качестве вспомогательных секущих плоскостей выбирают плоскости частного положения.
Слайд 9
Взаимное пересечение поверхностей (способ вспомогательных секущих плоскостей)
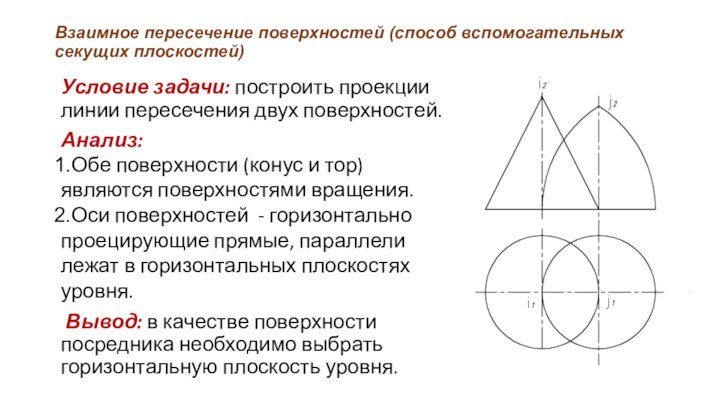
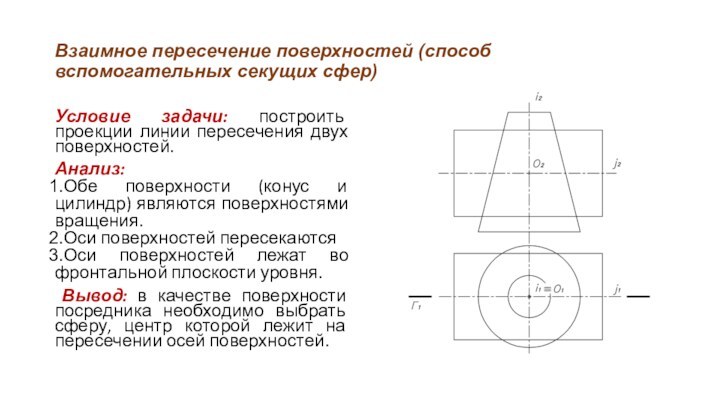
Условие задачи:
построить проекции линии пересечения двух поверхностей.
Анализ:
Обе поверхности (конус
и тор) являются поверхностями вращения.
Оси поверхностей - горизонтально проецирующие прямые, параллели лежат в горизонтальных плоскостях уровня.
Вывод: в качестве поверхности посредника необходимо выбрать горизонтальную плоскость уровня.
Слайд 10
Взаимное пересечение поверхностей (способ вспомогательных секущих плоскостей)
Решение задачи
Определяют
положение характерных точек.
Главные (фронтальные) меридианы лежат в одной плоскости
(фронтальной плоскости уровня) и пересекаются в точке А. Фронтальная проекция этой точки строится как точка пересечения фронтальных проекций меридианов, горизонтальная – по линии связи.
Основания поверхностей лежат в одной горизонтальной плоскости уровня и пересекаются в точке В и точке, ей симметричной. Горизонтальные проекции этих точек строятся как точки пересечения горизонтальных проекций оснований, фронтальные – по линии связи.
Слайд 11
Взаимное пересечение поверхностей (способ вспомогательных секущих плоскостей)
Решение задачи
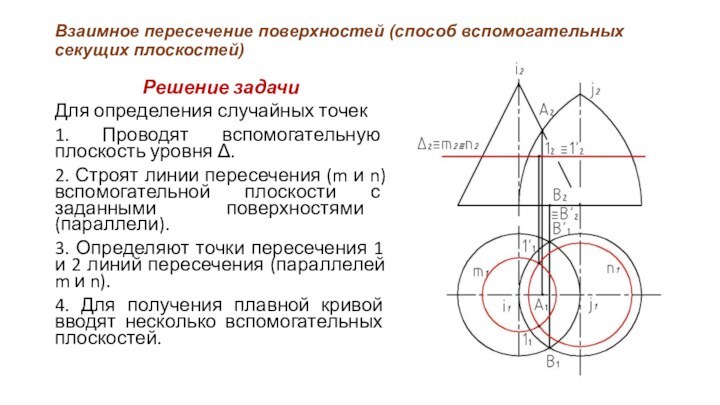
Для
определения случайных точек
1. Проводят вспомогательную плоскость уровня Δ.
2. Строят
линии пересечения (m и n) вспомогательной плоскости с заданными поверхностями (параллели).
3. Определяют точки пересечения 1 и 2 линий пересечения (параллелей m и n).
4. Для получения плавной кривой вводят несколько вспомогательных плоскостей.
Слайд 12
Взаимное пересечение поверхностей
Решение задачи
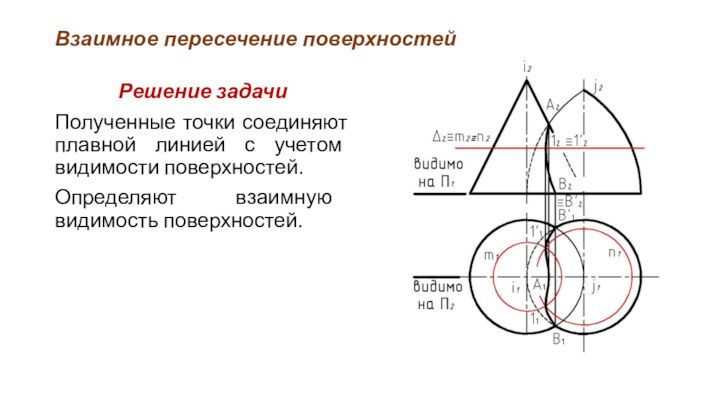
Полученные точки соединяют плавной линией
с учетом видимости поверхностей.
Определяют взаимную видимость поверхностей.
Слайд 13
Взаимное пересечение поверхностей
Если какая-либо из поверхностей является проецирующей,
то одна проекция линии пересечения определяется сразу (совпадает с
проекцией поверхности), а вторая строится по принадлежности точки и линии поверхности.
Слайд 14
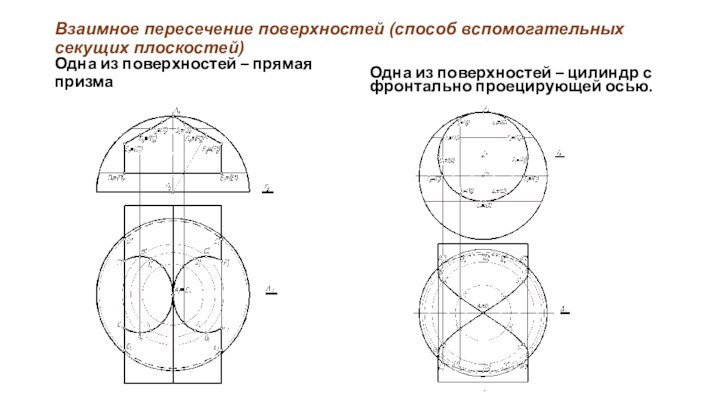
Взаимное пересечение поверхностей (способ вспомогательных секущих плоскостей)
Одна из
поверхностей – прямая призма
Одна из поверхностей – цилиндр с
фронтально проецирующей осью.
Слайд 15
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
Способ вспомогательных
секущих сфер применяют, если
обе поверхности являются поверхностями вращения и
их оси пересекаются (способ концентрических сфер) ;
если одна поверхность является поверхностью вращения, а вторая имеет параллельные между собой круговые сечения, центры которых лежат на одной линии, пересекающей ось поверхности вращения (способ эксцентрических сфер).
Слайд 16
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
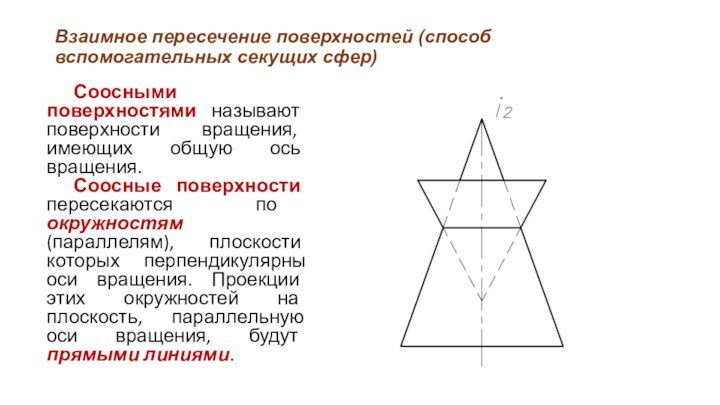
Соосными поверхностями
называют поверхности вращения, имеющих общую ось вращения.
Соосные поверхности
пересекаются по окружностям (параллелям), плоскости которых перпендикулярны оси вращения. Проекции этих окружностей на плоскость, параллельную оси вращения, будут прямыми линиями.
Слайд 17
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
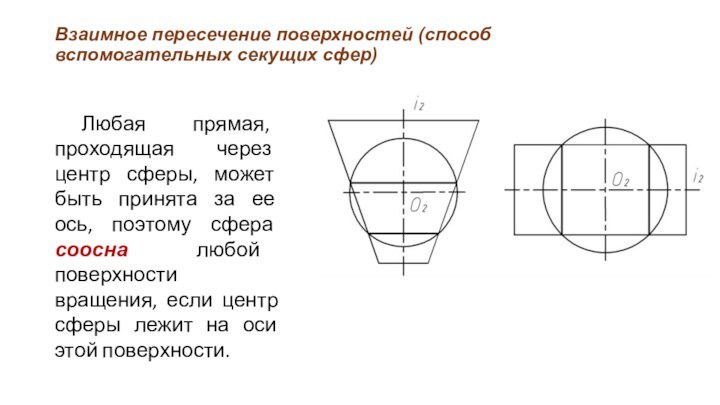
Любая прямая,
проходящая через центр сферы, может быть принята за ее
ось, поэтому сфера соосна любой поверхности вращения, если центр сферы лежит на оси этой поверхности.
Слайд 18
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
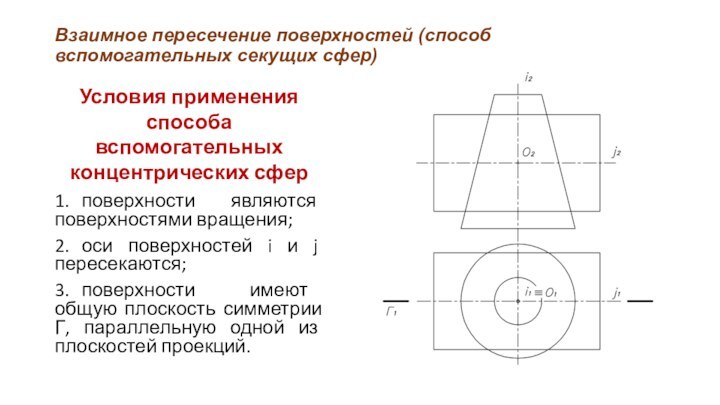
Условия применения
способа вспомогательных
концентрических сфер
1. поверхности являются поверхностями вращения;
2. оси поверхностей i
и j пересекаются;
3. поверхности имеют общую плоскость симметрии Г, параллельную одной из плоскостей проекций.
Слайд 19
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
Условие задачи:
построить проекции линии пересечения двух поверхностей.
Анализ:
Обе поверхности (конус
и цилиндр) являются поверхностями вращения.
Оси поверхностей пересекаются
Оси поверхностей лежат во фронтальной плоскости уровня.
Вывод: в качестве поверхности посредника необходимо выбрать сферу, центр которой лежит на пересечении осей поверхностей.
Слайд 20
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
Решение задачи
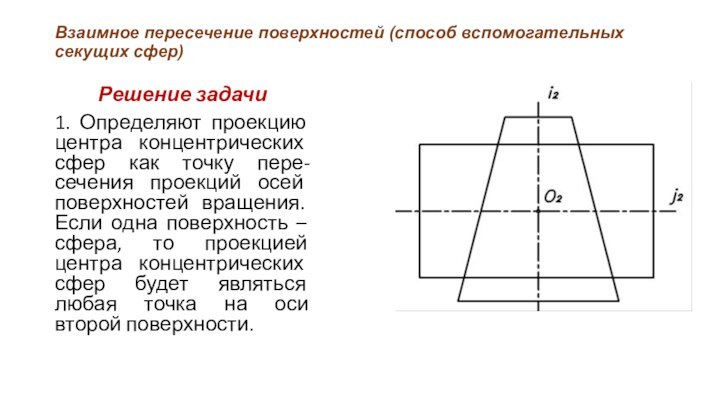
1.
Определяют проекцию центра концентрических сфер как точку пере-сечения проекций
осей поверхностей вращения. Если одна поверхность – сфера, то проекцией центра концентрических сфер будет являться любая точка на оси второй поверхности.
Слайд 21
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
Решение задачи
2.
Определяют и обозначают буквами точки пересечения главных меридианов (характерные
или опорные точки линии пересечения поверхностей)
Слайд 22
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
Решение задачи
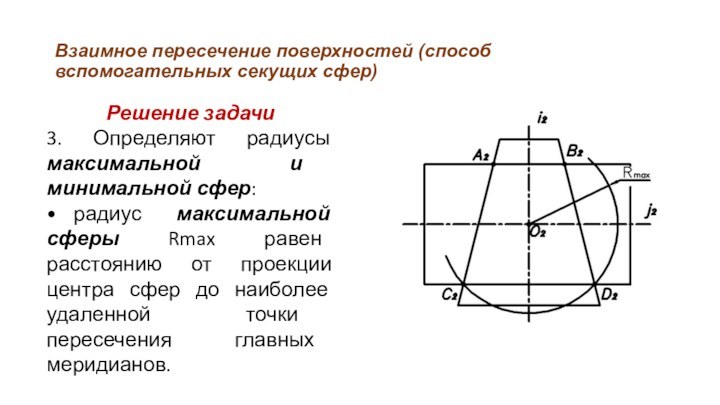
3.
Определяют радиусы максимальной и минимальной сфер:
• радиус максимальной сферы Rmax
равен расстоянию от проекции центра сфер до наиболее удаленной точки пересечения главных меридианов.
Слайд 23
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
Решение задачи
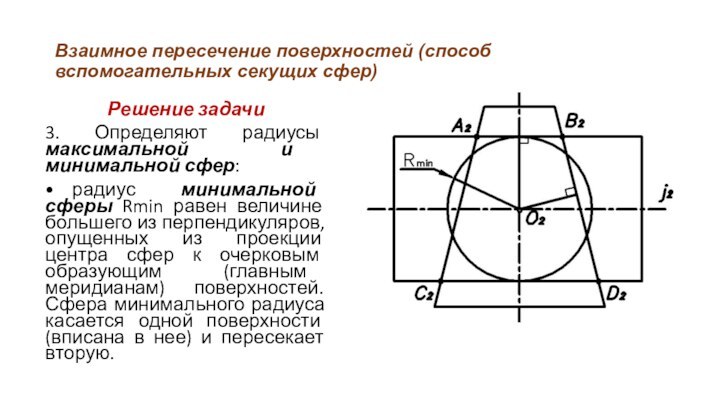
3.
Определяют радиусы максимальной и минимальной сфер:
• радиус минимальной сферы Rmin
равен величине большего из перпендикуляров, опущенных из проекции центра сфер к очерковым образующим (главным меридианам) поверхностей. Сфера минимального радиуса касается одной поверхности (вписана в нее) и пересекает вторую.
Слайд 24
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
Положение сферы
минимального радиуса задает направление проекций линии пересечения поверхностей относительно
проекций их осей.
Ветви кривых располагаются по разные стороны от оси той поверхности, которой касается сфера минимального радиуса.
Слайд 25
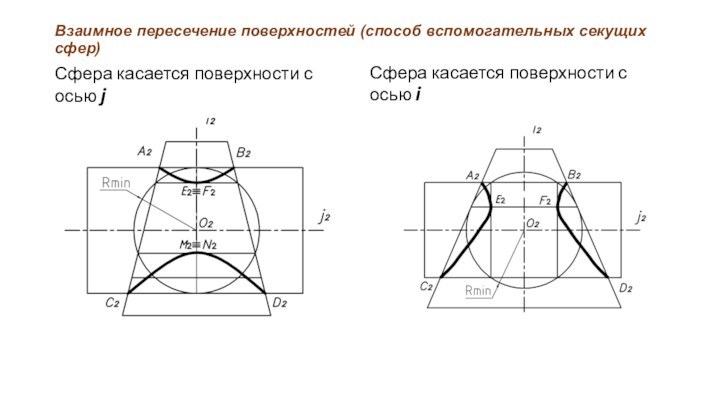
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
Сфера касается
поверхности с осью j
Сфера касается поверхности с осью i
Слайд 26
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
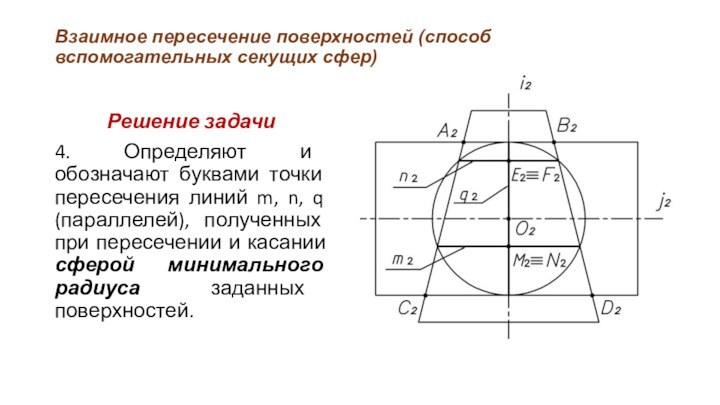
Решение задачи
4.
Определяют и обозначают буквами точки пересечения линий m, n,
q (параллелей), полученных при пересечении и касании сферой минимального радиуса заданных поверхностей.
Слайд 27
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
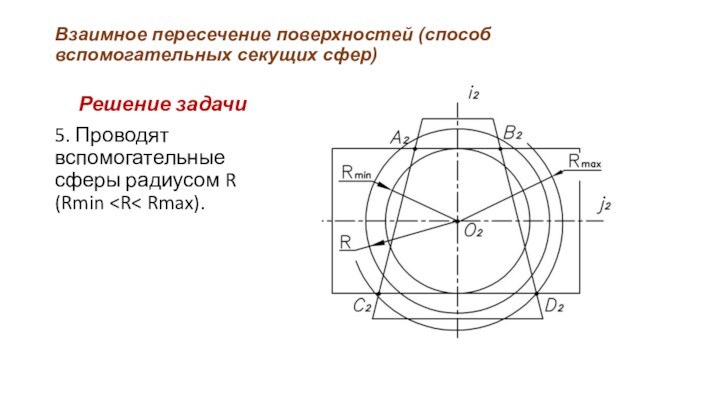
Решение задачи
5.
Проводят вспомогательные сферы радиусом R (Rmin
Слайд 28
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
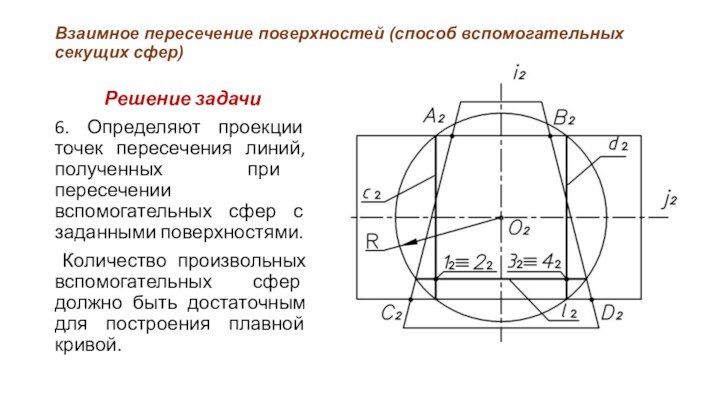
Решение задачи
6.
Определяют проекции точек пересечения линий, полученных при пересечении вспомогательных
сфер с заданными поверхностями.
Количество произвольных вспомогательных сфер должно быть достаточным для построения плавной кривой.
Слайд 29
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
Решение задачи
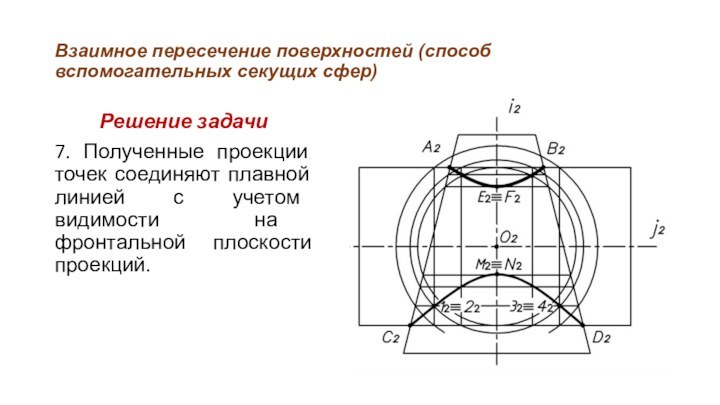
7.
Полученные проекции точек соединяют плавной линией с учетом видимости
на фронтальной плоскости проекций.
Слайд 30
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
Решение задачи
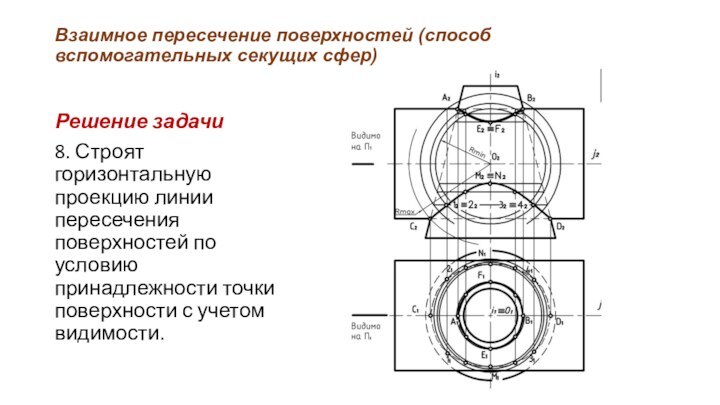
8.
Строят горизонтальную проекцию линии пересечения поверхностей по условию принадлежности
точки поверхности с учетом видимости.
Слайд 31
Взаимное пересечение поверхностей (способ вспомогательных секущих сфер)
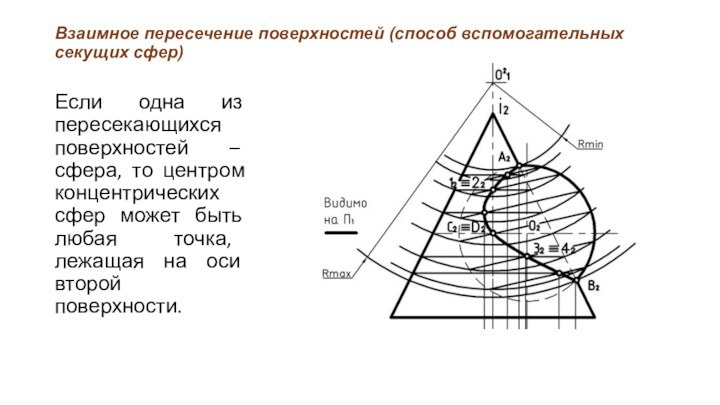
Если одна
из пересекающихся поверхностей – сфера, то центром концентрических сфер
может быть любая точка, лежащая на оси второй поверхности.