- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Задачи ЕГЭ по математике
Содержание
- 2. РазминкаЕсть квадрат со стороной 1.1) Согните чтобы получился отрезок: 2) Отрезок 1/33) Угол 30 градусов.
- 3. План встречиЗнакомство.Анализ результатов ЕГЭ 2012 года (отчет
- 4. О хорошем. Письмо МИНОБРа. "Неустановленные законодательством Российской
- 5. О хорошемЛетняя школа интенсивного обучения «Интеллектуал» для окончивших 7-8 класс.sch-int.ru/summer/
- 6. Структура варианта 2012-13 года14 задач группы В
- 7. Краткое описание задач.В1 – билеты, булки, процентыВ2
- 8. Краткое описание задач.В9 – стереометрия, вычислить, т.
- 9. Краткое описание задач.С1 – тригонометрическое уравнение с
- 10. Структура варианта 2012-13 гг
- 11. Сравнение результатов 2012 и 2011 годов (в
- 12. Сравнение результатов 2012 и 2011 годов (в
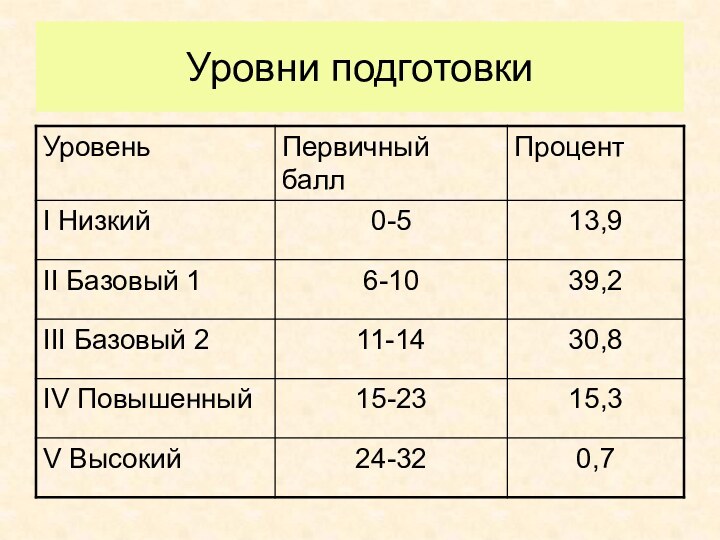
- 13. Уровни подготовки
- 14. Поступление в технические вузыКоличество бюджетных мест на
- 15. Низкий уровень подготовки. Основные задачи, которые решались:
- 16. Базовый уровень подготовки. Основные резервы.Две задачи по
- 17. Особенности выполнения задач группы С базовым уровнем
- 18. Как готовить класс к ЕГЭ? Методические и психологические соображения.
- 19. Условия для успешной сдачи экзаменаСпособности ученика.Мотивация ученика.Волевые
- 20. Психологические особенности подготовки к ЕГЭ. Личное мнение
- 21. Психологические особенности подготовки к ЕГЭ. Личное мнение
- 22. Содержание экзамена и учебникиСодержание экзамена только наполовину
- 23. Формы работы на уроке.Устный счетМатематические диктантыПоэлементная отработка (решение части задачи).«Листок» по сложным задачам.
- 24. Цели устного счетаПоддержка в рабочем состоянии всех
- 25. Целевая аудитория устного счета. Должна быть активна
- 26. Формы заданий устного счета.Серии задач с небольшим
- 27. Организация повторенияПри повторении увеличивается роль индивидуального подхода.
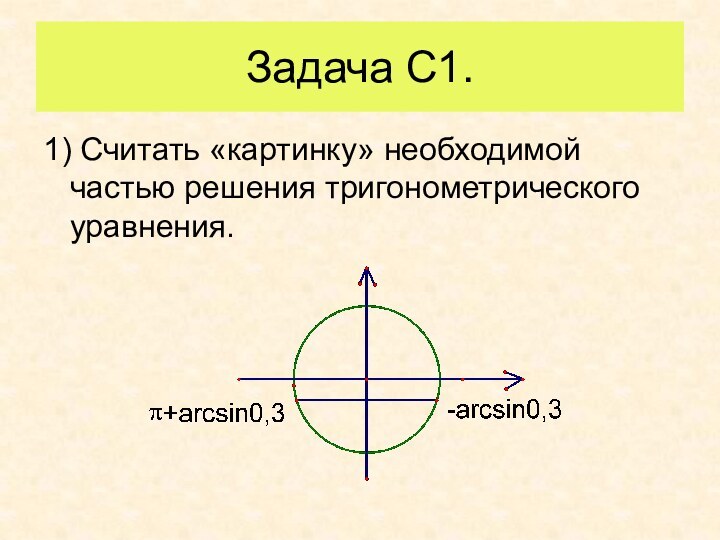
- 28. Задача С1.1) Считать «картинку» необходимой частью решения тригонометрического уравнения.
- 29. Задача С1.Не употреблять записьЭта запись не показывает:что
- 30. Задача С1.Давать отдельные задачи на отбор корней без решения уравнений.
- 31. Задача С1.Учиться проверять ответ. Для этого задавать
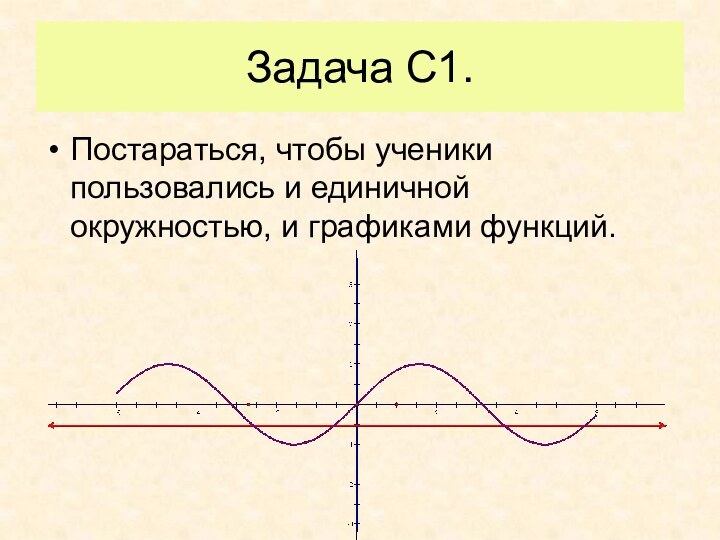
- 32. Задача С1.Постараться, чтобы ученики пользовались и единичной окружностью, и графиками функций.
- 33. Задача С2.Выбрать для повторения один объект (лучше
- 34. Задача С2.Задачи с одним объектом хороши тем,
- 35. С3. О неравенствах.Учиться решать системы неравенств в
- 36. О неравенствах. Полезно решать «обратные» задачи:Составлять неравенства
- 37. С 5. О задачах с параметром.Знакомить с
- 38. С 5. О задачах с параметром.Максимально использовать
- 39. Задача С5.Готовить для сильных учеников отдельные «листки»
- 40. Задача С6Борьба за «арифметический конструктив». Тип задач
- 41. Задача С6«Техника» работы с остатками должна завершать
- 42. Пример части первого листочка по С6: Число
- 43. Оформление решенияЗадача С1. В задаче есть два
- 44. Печатные и электронные ресурсыШкольные учебники.Пособия для подготовки
- 45. Скачать презентацию
- 46. Похожие презентации
РазминкаЕсть квадрат со стороной 1.1) Согните чтобы получился отрезок: 2) Отрезок 1/33) Угол 30 градусов.









































Слайд 3
План встречи
Знакомство.
Анализ результатов ЕГЭ 2012 года (отчет ФИПИ
и собственные соображения лектора).
О методике подготовки к ЕГЭ по
математике. Общие вопросы и разбор конкретных заданий. Печатные и электронные ресурсы.
Вопросы, реплики, обсуждения.
Слайд 4
О хорошем. Письмо МИНОБРа.
"Неустановленные законодательством Российской Федерации
или неурегулированные нормативными правовыми актами требования дополнительной информации от
общеобразовательного учреждения следует считать необоснованными.... в целях соблюдения установленного законодательством Российской Федерации разграничения полномочий между органами, осуществляющими управление в сфере образования, и недопущения нарушений законодательства Российской Федерации в области образования в части самостоятельности общеобразовательных учреждений Минобрнауки России сообщает о недопустимости по отношению к общеобразовательному учреждению следующих мер:
2. Запрос такого рода дополнительной информации, как планы работ методических объединений, отчёты о работе учителей-предметников, согласование учебных планов, а также учебных программ, образовательных программ, отчёты по участникам, победителям и призёрам различных олимпиад, конкурсов и тому подобное." (Из письма Минобрнауки от 12.09.2012 № ДЛ-150/08 «О сокращении объёмов и видов отчётности, представляемой общеобразовательными учреждениями»).
Слайд 5
О хорошем
Летняя школа интенсивного обучения «Интеллектуал» для окончивших
7-8 класс.
sch-int.ru/summer/
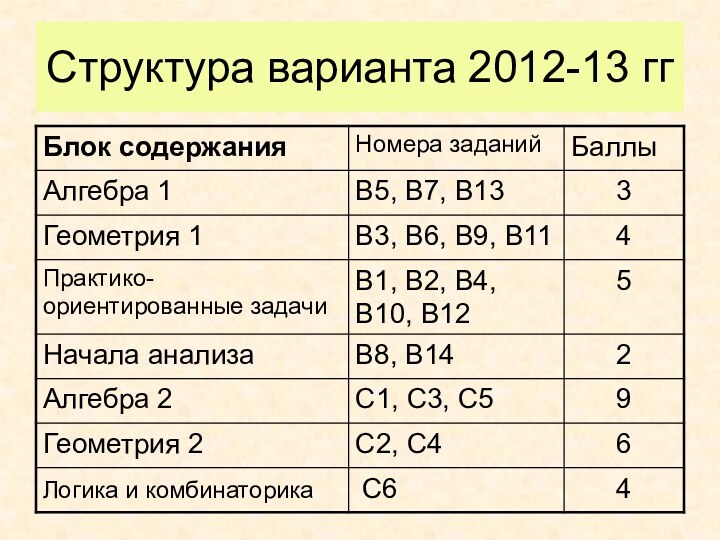
Слайд 6
Структура варианта 2012-13 года
14 задач группы В (по
1 баллу)
6 задач группы С:
С1 и С2 – по
2 балла.С3 и С4 – по 3 балла.
С5 и С6 – по 4 балла
Итого: 32 первичных баллов
Слайд 7
Краткое описание задач.
В1 – билеты, булки, проценты
В2 –
диаграмма (температура и т.п.)
В3 – площадь на клетчатой бумаге
В4
– три фирмы и ценыВ5 – простейшее уравнение
В6 – простая геометрия, угол
В7 – вычислить значение, в демоверсии – тригонометрия
В8 – производная, графическое задание
Слайд 8
Краткое описание задач.
В9 – стереометрия, вычислить, т. Пифагора
В10
– вероятность
В11 – стереометрия на понимание и наглядные соображения
В12 – математика в естествознании и экономике
В 13 – текстовая задача
В14 – мат. анализ, наибольшее значение на отрезке
Слайд 9
Краткое описание задач.
С1 – тригонометрическое уравнение с отбором
корней
С2 - стереометрия, найти угол, или расстояние
С3 – система
неравенствС4 – сложная планиметрия
С5 – задача с параметром
С6 – делимость, средние, логика
Слайд 11 Сравнение результатов 2012 и 2011 годов (в скобках)
В1 улучшение 89 % (81%)
В4 ухудшение 80 %
(87%) «три фирмы»В5 ухудшение 80 % (88%) уравнение
В8 сильное ухудшение 41% (64%) производная
В11 сильное ухудшение 37% (69%) стерео
В13 сильное ухудшение 50% (68%) текст. задача
В10 новая – 80 % вероятность
Остальные задачи почти также.
Слайд 12
Сравнение результатов 2012 и 2011 годов (в скобках)
«Положительный
результат», хотя бы один балл:
С1 – ухудшение 31% (42%)
С2 – резкое ухудшение 6% (14%)
С3 – ухудшение 12 % (20%)
С4 – ухудшение 2 % (4%)
С5 и С6 почти так же.
Слайд 14
Поступление в технические вузы
Количество бюджетных мест на технические
специальности и на специальность «учитель математики» значительно больше, чем
выпускников с повышенным уровнем знаний. На эти специальности зачислялись выпускники с базовым (2) уровнем.
Слайд 15
Низкий уровень подготовки.
Основные задачи, которые решались:
В1
(«билеты») ,
В2 («диаграмма»),
В3 («площадь – клетка»),
В4 («три
фирмы»), В5 (уравнение)
В10 (вероятность)
+В6 (планиметрия, углы),
+В9 (стереометрия, т. Пифагора)
Слайд 16
Базовый уровень подготовки. Основные резервы.
Две задачи по анализу:
В8 (37%) и В14 (39%).
Стереометрия на общее понимание:
В11
(32 %).Остальные задачи решали более половины базового уровня.
Базовый уровень хуже всего решил три задачи из первой части по программе 10-11 класса, требующие понимания, а не формальных действий.
Слайд 17 Особенности выполнения задач группы С базовым уровнем подготовки.
В задаче С1 верно решили тригонометрическое уравнение – 23%,
а
верно отобрали корни 8%.Остальные задачи меньше 3 % получили хотя бы по баллу за задачу.
Основной резерв – отбор корней.
Слайд 19
Условия для успешной сдачи экзамена
Способности ученика.
Мотивация ученика.
Волевые качества
и организационные способности ученика.
Качество преподавания.
От учителя зависит
только пункт 4) и частично пункт 3).
Слайд 20
Психологические особенности подготовки к ЕГЭ. Личное мнение лектора.
17-летние
юноши и девушки - давно не дети и многое
могут и должны делать сами:Определить цели при сдаче ЕГЭ (получить зачет, поступить в технический вуз или на математическую специальность).
Определить в начале учебного года собственный уровень подготовки и сформулировать свой план подготовки к ЕГЭ.
Находить пособия и сайты, которые им помогут.
Слайд 21
Психологические особенности подготовки к ЕГЭ. Личное мнение лектора.
Учитель
помогает молодым людям подготовиться к ЕГЭ, но не берет
всю ответственность на себя (даже, если эту ответственность на него возлагает начальство).Молодым людям крайне не полезно быть в роли детей, за которых кто-то взрослый отвечает. Тогда они расслабляются и ничего не хотят.
Слайд 22
Содержание экзамена и учебники
Содержание экзамена только наполовину покрывается
задачным материалом учебников 10-11 класса.
Учителя и ученики вынуждены
искать задачный материал вне учебников. Здесь помогают и пособия и разумные сайты.
Слайд 23
Формы работы на уроке.
Устный счет
Математические диктанты
Поэлементная отработка (решение
части задачи).
«Листок» по сложным задачам.
Слайд 24
Цели устного счета
Поддержка в рабочем состоянии всех пройденных
тем.
Обучение концентрации внимания.
Навык работы с задачами на разные
темы и разные алгоритмы («политематический набор задач»). Налаживание дополнительных связей внутри курса ( в частности, связей «картинка-формула»).
Слайд 25
Целевая аудитория устного счета.
Должна быть активна сильная
треть класса. Хорошо, когда подтягивается середина.
Слабые ученики на
устном счете получают опыт того, что они не знают, а также улавливают части решений, но учитель не тратит время на разжевывание. Ты понял, что забыл эту тему? Отлично! Вот учебник: повторяй.
Слайд 26
Формы заданий устного счета.
Серии задач с небольшим изменением
начальных условий, с целью получше вспомнить все нюансы темы.
Слайд 27
Организация повторения
При повторении увеличивается роль индивидуального подхода. Мы
вынуждены делить класс на подгруппы и давать разные задания
в зависимости от уровня подгруппы. Фронтальным образом иногда можно работать с серединой класса, самые слабые и самые сильные ученики должны получать свои задания.
Слайд 29
Задача С1.
Не употреблять запись
Эта запись не показывает:
что серий
решений две
Что период синуса 2П.
Отбирать корни при такой
форме записи крайне неудобно.
Слайд 31
Задача С1.
Учиться проверять ответ. Для этого задавать вопрос:
сколько корней данная серия решений может иметь на данном
отрезке.
Слайд 32
Задача С1.
Постараться, чтобы ученики пользовались и единичной окружностью,
и графиками функций.
Слайд 33
Задача С2.
Выбрать для повторения один объект (лучше всего
куб) и на нем найти все, что можно. Тем
самым решить несколько десятков задач на одну конструкцию.Начинать с совсем устных задач, и шаг за шагом усложнять.
Слайд 34
Задача С2.
Задачи с одним объектом хороши тем, что
сильные могут идти вперед, придумывая себе все более сложные
задачи.Удобно работать на готовых чертежах (отпечатанных на принтере листках), чтобы не тратить время урока на построение.
Слайд 35
С3. О неравенствах.
Учиться решать системы неравенств в 10
или 11 классе – поздно.
Естественное время для систем неравенств
– первое полугодие 9 класса. На чем можно сэкономить время?
Слайд 36
О неравенствах.
Полезно решать «обратные» задачи:
Составлять неравенства по
данному ответу, заданному в виде множества или картинки.
Это
один из лучших типов заданий для устного счета в старших классах.
Слайд 37
С 5. О задачах с параметром.
Знакомить с идейной
стороной задач с параметром нужно как можно раньше, самое
лучшее с 7 класса. Пример задачи:Исследуйте в каких четвертях в зависимости от b может располагаться точка пересечения графиков функций у=2х-4 и у=ах-2
Слайд 38
С 5. О задачах с параметром.
Максимально использовать геометрический
язык.
«В при изменении параметра…
…прямая двигается вдоль оси У
… вращается
вокруг точки……центр окружность двигается по прямой…
… изменяется величина угла (модуль)…
Слайд 39
Задача С5.
Готовить для сильных учеников отдельные «листки» по
задаче С5 с выстроенной последовательностью задач.
Каждая группа задач
на одну идею. Лучше для начала без сложной техники.
Слайд 40
Задача С6
Борьба за «арифметический конструктив». Тип задач с
такой формулировкой:
Приведите пример чисел, обладающих таким-то свойством…
Придумайте прогрессию,
у которой…
Слайд 41
Задача С6
«Техника» работы с остатками должна завершать экспериментирование
с целыми числами.
Нужно привить умение и привычку делать шаг
«посмотрим эту задачу с маленькими числовыми значениями и попробуем что-то увидеть».
Слайд 42
Пример части первого листочка по С6:
Число делится на
3. Верно ли, что его квадрат делится на 9?
Квадрат числа делится на 3. Верно ли, что само число делится на 3?
Квадрат числа делится на 9. Верно ли, что само число делится на 9?
Квадрат числа делится на 12. Что с уверенностью можно сказать про само число?
Какие остатки при делении на 3 может иметь квадрат целого числа?
Сумма квадратов двух чисел делится на 2. Верно ли, что она делится на 4?
Сумма квадратов двух чисел делится на 3. Верно ли, что она делится на 9?
Слайд 43
Оформление решения
Задача С1.
В задаче есть два задания:
а) решить тригонометрическое уравнение, б) отобрать его корни на
данном отрезке. Соответственно в ответе должно быть две части:а) все корни уравнения (не забудьте написать пресловутое n принадлежит Z),
б) отобранные на данном отрезке корни.
Важно написать именно так, чтобы при ошибке в отборе корней вам засчитали 1 балл за решение уравнения.
Решение уравнения лучше никак не комментировать и не писать знаков равносильности, так как часто при верном решении выпускники ошибаются в комментариях и ставят проверяющих в тупик.
Отбор корней, конечно, можно проводить разными способами, но рекомендуем его провести на окружности. Стоит иметь в виду, что в демоверсии он проведен на окружности, и с очень большой вероятностью так же он будет проведен и в решениях, которые раздадут проверяющим экспертам. Эксперту приятно, когда решение близко к присланному. Так сделайте ему приятное! При этом в начале отбора стоит написать фразу: отберем корни с помощью единичной окружности и затем обязательно на окружности все обозначить: точки – концы отрезка (в данном случае дуги), сами корни и жирным выделить саму дугу. Этот рисунок вы рисуете не для себя, а для проверяющего, на нем все должно быть видно.
При последней подготовке рекомендуем повторить или заново выучить формулы приведения – очень большой процент ошибок бывает именно в них, а так же решение простейших уравнений, обидно ошибиться в таких мелочах.
Слайд 44
Печатные и электронные ресурсы
Школьные учебники.
Пособия для подготовки к
ЕГЭ по математике.
mathege.ru (банк, задачи В)
reshuege.ru (с решениями и
есть С)ege.yandex.ru
(возможность протестироваться по группе В)
ege-go.ru/math-ege
(здесь советы по оформлению)